《Deep Learning on Graphs: A Survey》学习笔记【简略】
《Deep Learning on Graphs: A Survey》
《Deep Learning on Graphs: A Survey》。
Zhang Z, Cui P, Zhu W. Deep learning on graphs: A survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2020.
18年的一篇GNN综述,读完之后,感觉GCN那一部分对我帮助还不小,帮我理清了脉络,也可能是因为之前把《Graph Representation Learning》这本书看完了,所以阅读过程还比较顺利。后面的VGAE和图强化学习看的就比较粗,以后要是用到了再去看吧。
希望这篇笔记能够对后面的开题报告以及研究有所帮助吧。时间关系,只写一些对我近期可能有帮助的内容,毕竟本科毕设也不期望能搞出什么大事情,所以比较简略。
文章目录
- 《Deep Learning on Graphs: A Survey》
-
- Abstract
- 1 INTRODUCTION
- 2 NOTATIONS AND PRELIMINARIES
- 3 GRAPH NEURAL NETWORKS (GNNS)
- 4 GRAPH CONVOLUTIONAL NETWORKS (GCNS)
-
- 4.1 Convolution Operations
-
- 4.1.1 Spectral Methods
- 4.1.2 Efficiency Aspect
- 4.1.3 Multiple Graphs Aspect
- 4.1.4 Frameworks
- 4.2 Readout Operations
-
- 4.2.1 Statistics
- 4.2.2 Hierarchical clustering
- 4.2.3 Others
- 4.3 Improvements and Discussions
-
- 4.3.1 Attention Mechanism
- 4.3.2 Residual and Jumping Connections
- 4.3.3 Edge Features
- 4.3.4 Accelerating by Sampling
- 4.3.5 Inductive Setting
- 4.3.6 Random Weights
- 5 GRAPH AUTOENCODERS (GAES)
-
- 5.1 Autoencoders
- 5.2 Variational Autoencoders
- 5.3 Improvements and Discussions
-
- 5.3.1 Adversarial Training
- 5.3.2 Inductive Learning and GCN encoder
- 5.3.3 Similarity Measure
- 6 RECENT ADVANCEMENT
-
- 6.1 Graph Recurrent Neural Network
- 6.2 Graph Reinforcement Learning
- 7 CONCLUSION AND DISCUSSION
Abstract
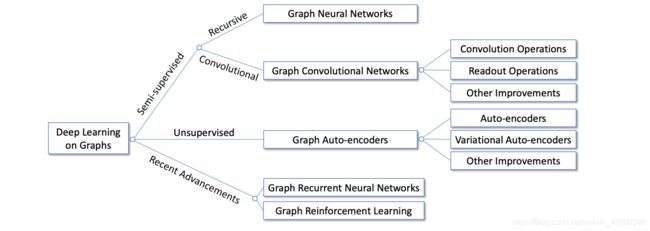
图数据无处不在,但是由于图数据自身结构的特殊性,对图数据应用深度学习方法有很多挑战。这篇综述主要是回顾各种图的深度学习模型,并将模型分为3类:
- 半监督方法:GNN、GCN
- 无监督方法:GAE
- 最新进展:Graph RNN、Graph RL
最后还会说一下模型的应用和未来发展方向。
1 INTRODUCTION
前面扯了一堆深度学习方法怎么怎么好、图数据又多么重要,其实就是想表达:我们非常需要使用DL方法研究图数据,但是有很多挑战和问题亟待解决,不然也不会有这篇文章了。几个挑战:
- 不规则域: 图数据没有像图片那样规则的网格结构,重新定义卷积、池化?
- 不同的任务和结构
- 可扩展性和并行性: 是否能扩展到大型图上面?时间复杂度是否可行?
- 交叉学科
之前也提到了,本文将模型分为3类。办监督的方法使用节点属性(特征)和标签来进行端到端训练;无监督方法使用GAE来进行表示学习;最新进展使用了其他独特的方法。

Related works.
主要说了一下图的DL方法和网络嵌入(Network embedding)的联系和区别。它们俩有交集:使用DL方法去做图的嵌入表示学习。但网络嵌入也可以不使用DL方法,图的DL方法也不只着眼于网络嵌入这个任务。
2 NOTATIONS AND PRELIMINARIES
符号表,2333,基本上看过一遍《Graph Representation Learning》都会对它们相当熟悉,即使换了一个“马甲”。

需要解决的任务主要分为2个领域:(其实我觉得应该分为3类。。)
- 节点级(node-level)任务:节点分类、 链接预测等。
- 图级(graph-level)任务:图分类、图生成等。
以 下 才 是 正 文 \color{#FF3030}{\boldsymbol{以下才是正文}} 以下才是正文
3 GRAPH NEURAL NETWORKS (GNNS)
本文把在卷积操作出现之前的方法单独视为GNN(半监督),但其实很多地方把所有使用DL方法学习图数据的模型,统称为GNN,还挺容易混淆的。
GNN和下一节的GCN十分相似,都使用了在邻居之间交换信息(MPNN)这一框架,不同之处在于早期GNN的每一层都不相同,而GCN的每一层都是相同的。
感觉对我没什么帮助,也不是重点,直接跳过一些细节。
4 GRAPH CONVOLUTIONAL NETWORKS (GCNS)
这一部分是我本次关注的重点!
还是老问题,很多地方把 「Kipf and Welling」 文章中的模型定义为GCN,而在本文中将使用了卷积操作的模型统称为GCN。
4.1 Convolution Operations
4.1.1 Spectral Methods
提到频域方法,第一反应应该想到这些名词:「拉普拉斯矩阵、图卷积、图傅里叶变换、滤波器」等等。学过通信DSP的相关知识可能会好一些,因为就是类比的信号处理,可惜cs专业并没有学过,现在一看到信号的傅里叶变换等概念就发蒙,只能先跳过去。
主要讲一下我自己对于图中的信号 u l ∈ R N u^l\in R^N ul∈RN(signal)和节点隐藏表示 h l ∈ R f l h^l\in R^{f^l} hl∈Rfl(hidden representation)的一些理解吧。
H l = [ ⋯ h l ⋯ ⋮ u l ⋮ ] , ∈ R N × f l H^l= \begin{bmatrix} &\cdots&h^l&\cdots\\ \vdots&&&\\ u^l&&&\\ \vdots&&&\\ \end{bmatrix},\in R^{N\times f^l} Hl=⎣⎢⎢⎢⎢⎡⋮ul⋮⋯hl⋯⎦⎥⎥⎥⎥⎤,∈RN×fl
从公式中可一直观的看到它们和隐藏层矩阵之间的关系。图中的信号可以看成是列,隐藏表示可以看作是行。一开始定义的各种变换和操作都是针对图信号的,经过后面的发展,逐渐演变成了适用于NN的隐藏表示的形式。
总之,通过图卷积操作(不熟悉的话看一下《GRL_Book》恶补一下),我们可以定义图信号的滤波操作,这也是后续各种空域(spatial)方法的基础。
u ′ = ( Q Θ ( Λ ) Q T ) u u'=\left(Q \Theta(\Lambda) Q^T\right)u u′=(QΘ(Λ)QT)u
在文章中 Θ \Theta Θ统一代表可学习的参数。
频域方法虽然产生了聚合邻域这一想法,但是有2个主要缺陷:
- L矩阵分解的时间复杂度至少 O ( N 2 ) O(N^2) O(N2),无法扩展大大型图上。
- 滤波器依赖于Q,参数无法在多个图中共享。
4.1.2 Efficiency Aspect
以下介绍的方法都是空域(spatial)方法。
一个比较经典的模型是ChebNet。后面需要重点阅读。
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering[J]. arXiv preprint arXiv:1606.09375, 2016.
它的主要思想是多项式滤波器+切比雪夫展开:
Θ ( Λ ) = ∑ k = 0 K − 1 θ k T k ( Λ ~ ) u ′ = ∑ k = 0 K − 1 θ k T k ( L ~ ) u = ∑ k = 0 K − 1 θ k u ‾ k \Theta(\Lambda)=\sum_{k=0}^{K-1}\theta_k \mathcal T_{k}(\tilde \Lambda)\\ u'=\sum_{k=0}^{K-1}\theta_k\mathcal T_{k}(\tilde L)u=\sum_{k=0}^{K-1}\theta_k \overline u_k Θ(Λ)=k=0∑K−1θkTk(Λ~)u′=k=0∑K−1θkTk(L~)u=k=0∑K−1θkuk
最后简化到了这个程度,并且 u ‾ k \overline u_k uk还可以通过递推式子得到。时间复杂度降到了 O ( K M ) O(KM) O(KM),并且每次滤波(卷积)相当于聚合了每个节点的K跳邻居信息。
最经典的空域卷积模型莫过于Kipf and Welling文章中提到的GCN模型了。后面需要重点阅读。
Kipf T N, Welling M. Semi-supervised classification with graph convolutional networks[J]. arXiv preprint arXiv:1609.02907, 2016.
它简化了滤波器,每次卷积只聚合一阶(直接)邻居信息(相当于K=1),并且使用了对称标准化+自循环更新。写成矩阵的形式,就开始有了NN的味道了。
H l + 1 = ρ ( ( D ~ − 1 2 A ~ D ~ − 1 2 ) H l Θ l ) H^{l+1}=\rho\left((\tilde D^{-\frac12}\tilde A\tilde D^{-\frac12})H^l\Theta^l \right) Hl+1=ρ((D~−21A~D~−21)HlΘl)
之前在笔记中多次提到过GCN,在这里就不多说了。
4.1.3 Multiple Graphs Aspect
如果需要训练多个不同大小的图,并且想在训练的时候让不同的图参数共享,可以使用这一部分介绍的模型。
然而,我看了一下那几个引文网络数据集,发现图的数量都是1,那么就没有这部分什么事了,就不写笔记了。
4.1.4 Frameworks
主要介绍了主流的消息传递框架MPNN,和《GRL_Book》中提到的差不多,有时间需要看一下。
Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[J]. arXiv preprint arXiv:1704.01212, 2017.
大体上比较熟了,懒得再写一遍了。文章提到了添加一个和所有节点全连接的"master" node,来加速长距离的消息传递,这一点之前没有注意到。
接下来,是经常被用来进行实验的GraphSAGE模型,里面的消息传递操作也相当经典。后面需要重点阅读。
Hamilton W, Ying Z, Leskovec J. Inductive representation learning on large graphs[C]//Advances in neural information processing systems. 2017: 1024-1034.
基本就是根据MPNN框架照猫画虎,消息传递操作如下:
m i l + 1 = A g g r e g a t e l ( { h j l , ∀ j ∈ N ( i ) } ) h i l + 1 = ρ ( Θ l [ h i l ⊕ m i l + 1 ] ) m_i^{l+1}=Aggregate^l\left(\{h_j^l,\forall j\in N(i)\}\right)\\[2ex] h_i^{l+1}=\rho \left(\Theta^l[h_i^l\oplus m_i^{l+1}]\right) mil+1=Aggregatel({hjl,∀j∈N(i)})hil+1=ρ(Θl[hil⊕mil+1])
更新函数没什么新东西,顶多是拼接操作新奇一点(可能借鉴了跳跃连接?);给出了3个聚合函数:
- 逐元素平均
- LSTM:这个需要给节点排序,不知道如何保证排列不变性的?
- max池化
后面也有介绍GN这样更通用(更吓人)的一般性框架,暂且搁置吧。
最常见的选择是改进版本的GCN卷积层+MPNN框架。
4.2 Readout Operations
这部分说白了就是池化操作,在GNN中美其名曰readout。它将所有节点的嵌入表示进行池化得到整张图的嵌入表示,然后再拿着这个图级表示,去做一些诸如图分类这样的任务。
Order invariance
顺序不变性,或者说排列不变性,这是一个老生常谈的问题了。通俗来说就是,同一张图的各种矩阵,不论它们最初的节点排列顺序是怎样的,最终学习出来的图级表示必须是相同的。这部分和图同构测试也有一些关系。
4.2.1 Statistics
满足排列不变性+能聚合所有节点嵌入表示最简单的方法是直接sum,max或average。也就是说,通过对最后一层得到的节点嵌入表示进行上述简单的操作,就可以得到图级表示。但由于它过于简单粗暴,就导致损失了很多结构信息。
当然,还有一些带参数的方法,但也都是大同小异,表达能力有限。
4.2.2 Hierarchical clustering
另一种方法是层次聚类,它一般和之前的卷积层一起进行端到端的训练。
比较早的池化模型是DiffPool。后面需要重点看一下。
Ying Z, You J, Morris C, et al. Hierarchical graph representation learning with differentiable pooling[C]//Advances in neural information processing systems. 2018: 4800-4810.
它的主要思想是,学习簇分配矩阵S,然后通过S去得到一个坍缩后的图(新的A和X),重复这个过程直至收敛。每次进行坍缩,图的簇数都会减少。
关于这个模型,之前的笔记说的也比较清楚了,不再详细展开。
4.2.3 Others
其他方法,比如说增加一个代表整张图的特殊节点等。
一般来说,前两种方法出现的比较多。
4.3 Improvements and Discussions
一些改进策略(大方向),对于某些模型的改进可能会有一些帮助。
4.3.1 Attention Mechanism
不同重要程度的邻居需要区别对待,聚合的时候来一个加权操作,这就是注意力机制。
在实践中,将所有邻居同等对待或人为去指定哪个节点更重要,往往不太行。注意力机制是一个比较好的改进思路。
最早的图注意力模型是GAT。后面需要重点看一下。
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017.
它主要的各种变体都是如何去计算注意力权重 α i j \alpha_{ij} αij。此外,它还提出了多头注意力机制。这个模型,之前的笔记也写过,不再进行展开。
4.3.2 Residual and Jumping Connections
一方面是受到了ResNet的启发,一方面是模型存在过平滑的问题,冗余连接/跳跃连接开始被应用于GNN的模型中。
在GCN模型中,Kipf and Welling也引入了冗余连接,以保留上一层的结果。这样做可以缓解过平滑问题,增加模型的深度。
H l + 1 = ρ ( ( D ~ − 1 2 A ~ D ~ − 1 2 ) H l Θ l ) + H l H^{l+1}=\rho\left((\tilde D^{-\frac12}\tilde A\tilde D^{-\frac12})H^l\Theta^l \right)+H^l Hl+1=ρ((D~−21A~D~−21)HlΘl)+Hl
CLN模型看起来更聪明一点,类似于一种加权求和,权重是可学习的参数。
Pham T, Tran T, Phung D, et al. Column networks for collective classification[J]. arXiv preprint arXiv:1609.04508, 2016.
h i l + 1 = α i l ⊙ h ~ i l + 1 + ( 1 − α i l ) ⊙ h i l h_i^{l+1}=\alpha_i^l \odot \tilde h_i^{l+1}+(1-\alpha_i^l)\odot h_i^l hil+1=αil⊙h~il+1+(1−αil)⊙hil
JK-Nets把最后一层和之前的所有层都进行一个连接,得到最终的嵌入表示。
Xu K, Li C, Tian Y, et al. Representation learning on graphs with jumping knowledge networks[J]. arXiv preprint arXiv:1806.03536, 2018.
实验表明,添加跳跃连接是改进模型表达能力的一个很好的方法。
4.3.3 Edge Features
这些策略一般用在多关系图中,暂时还用不到,溜了。
4.3.4 Accelerating by Sampling
在大规模图上,效率问题一直是瓶颈,特别是在模型很复杂的时候。在一个十几亿级别的图上,如果你还企图搞个 O ( N 2 ) O(N^2) O(N2)的操作,那真是太naive了。基本上,还是需要通过牺牲一些信息进行采样,来达到效率和表达能力之间的权衡。
在《GRL_Book》的第8章中提到过,其实真实图中的节点度是服从幂律分布的。也就是说,总会有极个别度数超级高的节点,它们邻居节点数量的增长速度十分吓人。
GraphSAGE采样固定数量的邻居节点,PinSage使用随机游走方法采样邻居节点。
另一种不同的策略是FastGCN模型。
Chen J, Ma T, Xiao C. Fastgcn: fast learning with graph convolutional networks via importance sampling[J]. arXiv preprint arXiv:1801.10247, 2018.
它从积分变换的角度来看问题,听起来就很高端:将节点解释为符合 i . i . d . i.i.d. i.i.d.的样本,图卷积操作看作是积分变换。有时间再去看一下paper,根本不知道它在说什么。
4.3.5 Inductive Setting
我觉得解释为归纳学习好理解一点。归纳学习的典型特点:训练时使用带标签的 V t r a i n V_{train} Vtrain,测试时使用训练时不可见的 V i n d V_{ind} Vind。
GraphSAGE、GAT、FastGCN等模型都属于归纳GCN模型,它们训练的也都是有特征的图。
4.3.6 Random Weights
通过设置随机权重,未经训练的GCN模型也可以提取到有意义的节点特征?
5 GRAPH AUTOENCODERS (GAES)
AE属于无监督学习的范畴,在图中一般称为GAE。这些模型的架构都离不开编解码器模型,《GRL_Book》对这个框架中介绍的相当详细了。

5.1 Autoencoders
这一部分有一些学习节点嵌入表示的模型还是很有参考价值的,因此,直接列举几个姑且、可能对我毕设有帮助的几个模型。
结构化的深层嵌入网络SDNE模型。
Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 1225-1234.
编码器使用了GCN的GC-MC模型。
Berg R, Kipf T N, Welling M. Graph convolutional matrix completion[J]. arXiv preprint arXiv:1706.02263, 2017.
5.2 Variational Autoencoders
之前看了好几次VGAE模型都没有看懂,现在发现遇到的次数多了,好像也慢慢有点感觉了?!
Kipf T N, Welling M. Variational graph auto-encoders[J]. arXiv preprint arXiv:1611.07308, 2016.
那几个后验分布还是让我有点晕头转向,之前的笔记也有写过这个。
它的encoder使用了2个独立的GNN,分别去计算嵌入表示H的均值和方差,以便使用高斯(正态)分布进行H的采样。decoder说是要算后验概率 P ( A ∣ H ) P(A|H) P(A∣H),其实在VGAE中也就是使用了简单的内积解码器。最后就是那个带有KL散度的特别恶心的loss。
其他模型都是对VGAE做出的改进,直接忽略了,还是要慢慢来。
5.3 Improvements and Discussions
对GAE的一些改进措施。
5.3.1 Adversarial Training
使用生成对抗网络GAN(就是淦),进行对抗训练。把encoder看作是generator,然后使用discriminator区分到底是假的还是真的。这种极大极小联合优化感觉还蛮困难的,之前也有看到很过模型的名字后面都会加一个GAN。
5.3.2 Inductive Learning and GCN encoder
encoder使用GCN可以继承GCN归纳学习的良好性质。很多模型都会将GAE和GCN结合使用,效果更好。
5.3.3 Similarity Measure
如何选择相似性度量,目前还没有清晰的判断依据。
6 RECENT ADVANCEMENT
6.1 Graph Recurrent Neural Network
Graph RNN将RNN的知识用到了图的层面。
6.2 Graph Reinforcement Learning
Graph RL主要用到了强化学习的一些知识。
7 CONCLUSION AND DISCUSSION
总结并没有什么东西。主要介绍了一下应用和未来方向。
- 如何处理不同类型的图。同构、异构图,有符号图,超图等等。
- 如何处随时间变化的动态图。
- 在其他学科领域的可解释性。
- 如何有效地组合各种模型架构。