计算机视觉实战基础(3)图像金字塔与采样
目录
一、引言
二、插值
1、最邻近插值
2、双线性插值
3、open-cv的插值代码
三、下采样
1、理论
2、代码实现
一、引言
先请大家看一张长宽各为32像素(px)的照片:
![]()
我猜不少的读者这时都会吐槽:What!这是啥玩意儿啊,小编,你又不怀好心了?给我们看这种图片,我能看得清吗?
哈哈哈,小编当然是故意的啦。小编想提出的问题是,看不清这张图片,我们自然而然的会选择将它放大很多倍。比如说长宽各放大5倍,也就是160px,那么这些多出来的像素,我们该如何去填充?
比如说下面这张图,我们放大后,只能确定几个“角”的颜色的像素值,而其他空虚的像素,用什么颜色去“填充”就显得至关重要,这就要引出我们今天的主角------------插值,也叫做上采样。
二、插值
我们有很多种插值方法,下面小编将会分别介绍其原理及其实现代码。
1、最邻近插值
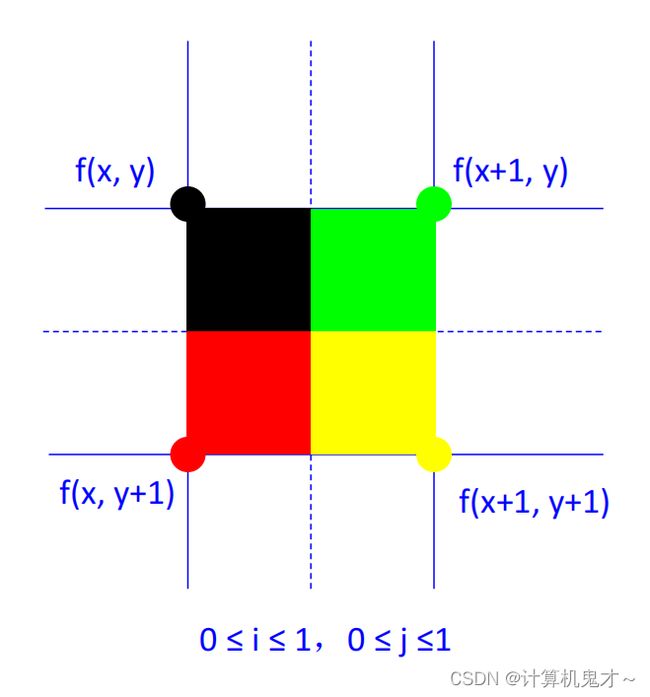
根据名字,读者应该就已经能猜出个大概了。所谓“最邻近”无非就是用最靠近该未知点的已知像素值填充这个点。其原理如下图:
原理:将空间上最近邻的已知像素值赋给未知像素
如果i≤0.5, j≤0.5,则 f(x+i, y+j) = f(x, y) ;
如果i>0.5, j≤0.5,则 f(x+i, y+j) = f(x+1, y) ;
如果i≤0.5, j>0.5,则 f(x+i, y+j) = f(x, y+1) ;
如果i>0.5, j>0.5,则 f(x+i, y+j) = f(x+1, y+1) ;
2、双线性插值
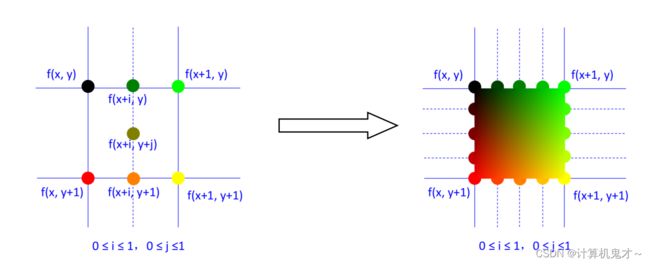
所谓双线性,“双”指的是两个方向,也就是水平方向和垂直方向。它克服了最邻近插值算法“格子化”严重的缺点,赋予了每个未知像素点一个权重去计算像素值。如下图:
原理:在x,y两个方向进行线性插值,由已知像素值加权合成未知像素值;
未知与已知像素距离越近,权重越大
x方向线性插值:
f(x+i,y) = (1-i)* f(x,y) + i* f(x+1,y) ;
f(x+i,y+1) = (1-i)* f(x,y+1) + i* f(x+1,y+1) ;
y方向线性插值: f(x+i,y+j) = (1-j)* f(x+i,y) + j* f(x+i,y+1) ;
3、open-cv的插值代码
尽管我相信各位读者有能力去写一段代码完成上述两种插值运算,但其实open-cv自带了插值算法,我们只需要调用这个函数即可,正所谓又便宜不占,不是王八蛋吗。毕竟谁愿意每次写那么一大串代码就只是为了插值运算?
dst=cv2.resize(src, dsize[,fx[, fy[, interpolation]]])
参数介绍:
dst:目标图像
src:原图像在open-cv2中的名字
dsize:输出图像所需大小,以坐标的形式表出,如(320,320)
fx:沿水平轴的比例因子,如果dsize不为None,则以dsize为主
fy:沿垂直轴的比例因子,同上
interpolation:插值方式,其值如下图所示
interpolation的可选值为:
cv.INTER_NEAREST:最近邻插值
cv.INTER_LINEAR:双线性插值
cv.INTER_CUBIC:基于4x4像素邻域的3次插值法
cv.INTER_AREA:基于局部像素的重采样
我们拿lena的小图片练练手,以最邻近法进行插值,其代码段如下:
import cv2
import numpy as np
import random
img=cv2.imread("lena_LR.png",-1)
#dsize=(320,320)等价于dsize=None,fx=10,fy=10
img1=cv2.resize(img,dsize=(320,320),fx=10,fy=10,interpolation=cv2.INTER_NEAREST)
cv2.imshow('nearest_resize',img1)
cv2.imwrite('picture1.png',img1)
cv2.waitKey()
cv2.destroyAllWindows()得到的最邻近插值图像如下图:
三、下采样
1、理论
既然有上采样(插值),那么自然而然的,也会有下采样。上采样应用于图片放大,对应的下采样应用于图片缩小。比如说,下面这张梵高的自画像忒大了,以至于不适合这张屏幕了,我们自然而然的想要去缩小。
当我们将长与宽个自缩小为原来的一半时,我们很容易想到,对于微观的像素,我们只需要同时删除奇数行和奇数列,保留偶数行和偶数列;或者同时删除偶数行偶数列,保留奇数行和奇数列即可。说干就干,其缩小过程如下图:
但是,当你仔细端详缩小后的图片后,你会发现,怎么会这么难看?这就要提到一个概念了———走样。走样发生在当采样率不足以捕捉图像大量细节的时候,每次走样可能给你错误的图像或者信号。生活中最常见的走样是车子在往前跑,我们用眼睛去观察车轮的时候,我们总感觉这轮子是往后转的。是不是很有意思?也就是说,车跑的太快了,以至于我们的眼睛无法去及时的捕捉轮子的特征,采样率就自然而然的下降了,给了我们一个错误的信号。
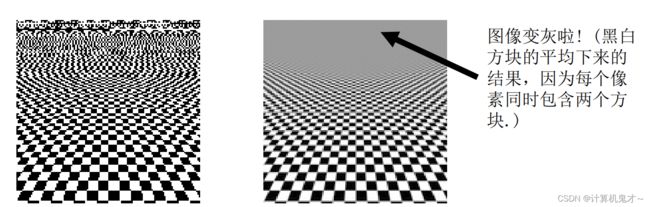
“小细节”太多,会导致电脑不知道图片缩小后,拿哪一个点的像素值去填充。而在频域中,小细节对应的是高频区,这就意味着如果我们能将高频降低为低频,也就不会出现这种特别“难看”的模糊了。所以下采样不仅仅只是下采样,而是先进行高斯滤波模糊,再进行下采样。这样得到的结果如下图:
下面这张图可能看的更加直观一点,左边为未高斯滤波而导致最上边的部分走样了,看着极度不舒适,右图是高斯滤波后再进行采样的结果。
2、代码实现
dst=cv2.pyrDown(src,[,dstsize[,borderType]]])
参数介绍:
dst:目标图像
src:原图像在open-cv中的名字
dstsize:目标图像大小(默认长宽各减少一半)
borderType:边缘类型,这个可以看小编写的上一篇文章
实战一波,我们将输出一张指定图片的四分之一大小与十六分之一大小,代码如下:
import cv2
import numpy as np
img=cv2.imread("test1.jpg",-1)
#img1为缩小为1/4的图
img1=cv2.pyrDown(img)
#img2位缩小为1/16的图
img2=cv2.pyrDown(img1)
cv2.imshow('half',img1)
cv2.imshow("one_forth",img2)
cv2.imwrite('picture1.png',img1)
cv2.imwrite("picture2.png",img2)
cv2.waitKey()
cv2.destroyAllWindows()
输出的两张小图如下:
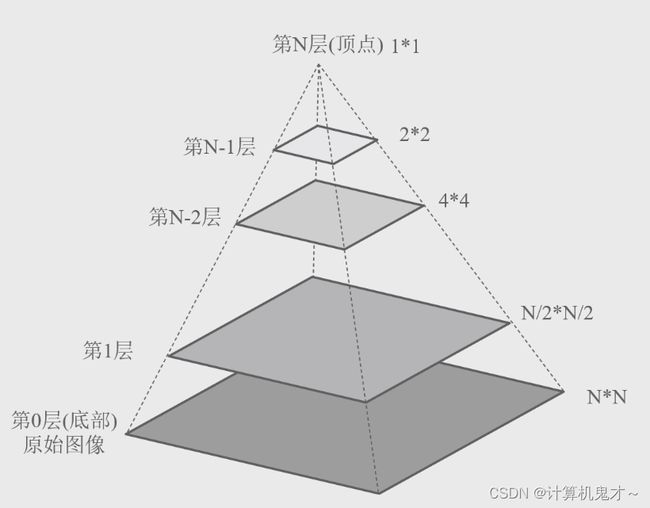
是不是很有意思,是不是小编今天不提到图像的放大与缩小,各位读者可能也不会想到我们平常随手放大与缩小的图片,竟然藏了这么多学问?与此同时,我们把今天所学到的这些知识合称为图像金子塔,如下图,通过今天的学习,我们要既能让图片从顶点到底点进行上采样,也能从底点到顶点实现下采样。
好了,本期的计算机视觉内容就到这里啦,如果对本篇文章比较满意的话,请一键三连,小编将带你学习更多的计算机领域知识。