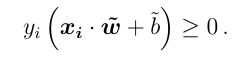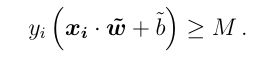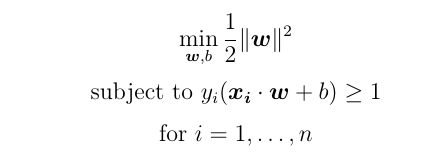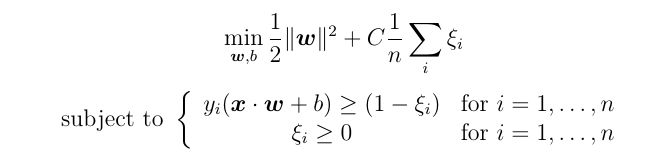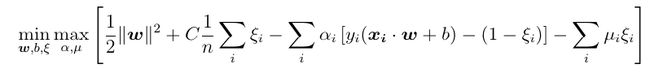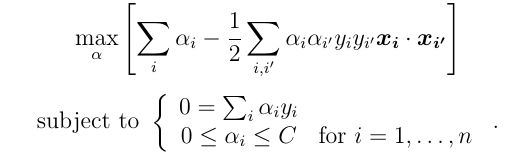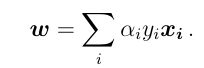支持向量机回归和支持向量机
Support Vector Machine(SVM) is a supervised machine learning algorithm that is usually used in solving binary classification problems. It can also be applied in multi-class classification problems and regression problems. This article represents the mathematics behind the binary-class linear Support Vector Machines. Understanding mathematics helps implement and tune the models in practice. Moreover, you can build your own support vector machine model from scratch, and compare it with the one from Scikit-Learn. For details, you can read this article along with another article of mine.
支持向量机(SVM)是一种监督型机器学习算法,通常用于解决二进制分类问题。 它也可以应用于多类分类问题和回归问题。 本文介绍了二元类线性支持向量机背后的数学原理。 了解数学有助于在实践中实现和调整模型。 此外,您可以从头开始构建自己的支持向量机模型,并将其与Scikit-Learn的模型进行比较。 有关详细信息,您可以阅读本文以及我的另一篇文章。
Specifically, this report explains the key concepts of linear support vector machine, including the primal form and its dual form for both hard margin and soft margin case; the concept of support vectors, max-margin, and the generalization process.
具体而言,本报告解释了线性支持向量机的关键概念,包括硬边际和软边际情况的原始形式及其对偶形式; 支持向量,最大边距和归纳过程的概念。
Key Concepts of SVM
SVM的关键概念
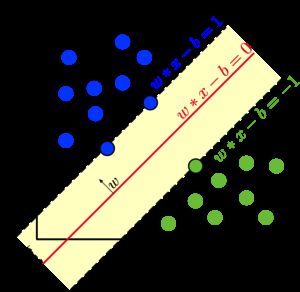
Assume we have n training points, each observation i has p features (i.e. x_i has p dimensions), and is in two classes y_i=-1 or y_i = 1. Suppose we have two classes of observations that are linearly separable. That means we can draw a hyperplane through our feature space such that all instances of one class are on one side of the hyperplane, and all instances of the other class are on the opposite side. (A hyperplane in p dimensions is a p-1 dimensional subspace. In the two-dimensional example that follows, a hyperplane is just a line.) We define a hyperplane as:
假设我们有n个训练点,每个观测值i具有p个特征(即x_i具有p个维),并且处于两类y_i = -1或y_i =1。假设我们有两类线性可分离的观测值。 这意味着我们可以在特征空间中绘制一个超平面,这样一类的所有实例都在超平面的一侧,而另一类的所有实例都在另一侧。 (p维上的超平面是p-1维子空间。在下面的二维示例中,超平面只是一条线。)我们将超平面定义为:
where ˜w is a p-vector and ˜b is a real number. For convenience, we require that ˜w = 1, so the quantity x * ˜w + ˜b is the distance from point x to the hyperplane.
其中〜w是p向量,〜b是实数。 为了方便起见,我们要求〜w = 1,所以数量x *〜w +〜b是从点x到超平面的距离。
image from Wikipedia 图片来自维基百科Thus we can label our classes with y = +1/-1, and the requirement that the hyperplane divides the classes becomes:
因此,我们可以用y = + 1 / -1标记我们的类,超平面划分这些类的要求变为:
How should we choose the best hyperplane?
我们应该如何选择最佳的超平面?
The approach to answering this question is to choose the plane that results in the largest margin M between the two classes, which is called the Maximal Margin Classifier.
回答此问题的方法是选择在两个类别之间产生最大边距M的平面,这称为最大边距分类器。
image from Wikipedia 图片来自维基百科From the previous graph, we can see that H1 doesn’t separate the two classes; for H2 and H3, we will choose H3 because H3 has a larger margin. Mathematically, we choose ˜b and ˜w to maximize M, given the constraints:
从上一张图中,我们可以看到H1并没有将这两个类别分开。 对于H2和H3,我们将选择H3,因为H3具有较大的边距。 在数学上,给定约束,我们选择〜b和〜w以最大化M:
Defining w =˜ w / M and b =˜b / M, we can rewrite this as:
定义w = 〜w / M和b =〜b / M ,我们可以重写为:
and
和
The support vectors
支持向量
The support vectors are the data points that lie closest to the separating hyperplane. They are the most difficult data points to classify. Moreover, support vectors are the elements of the training set that would change the position of the dividing hyperplane if removed. The optimization algorithm to generate the weights proceeds in such a way that only the support vectors determine the weights and thus the boundary. Mathematically support vectors are defined as:
支持向量是最靠近分离超平面的数据点。 它们是最难分类的数据点。 此外,支持向量是训练集的元素,如果被移除,它们将改变划分超平面的位置。 生成权重的优化算法以这样的方式进行:只有支持向量才能确定权重,从而确定边界。 数学上的支持向量定义为:
Hard-margin SVM
硬利润支持向量机
The hard-margin SVM is very strict with the support vectors crossing the hyperplane. It doesn’t allow any support vectors to be classified in the wrong class. To maximize the margin of the hyperplane, the hard-margin support vector machine is facing the optimization problem:
硬边支持向量机非常严格,支持向量跨过超平面。 不允许将任何支持向量分类为错误的类。 为了最大化超平面的余量,硬余量支持向量机面临着优化问题:
Soft-margin SVM and the hyper-parameter C
软边距SVM和超参数C
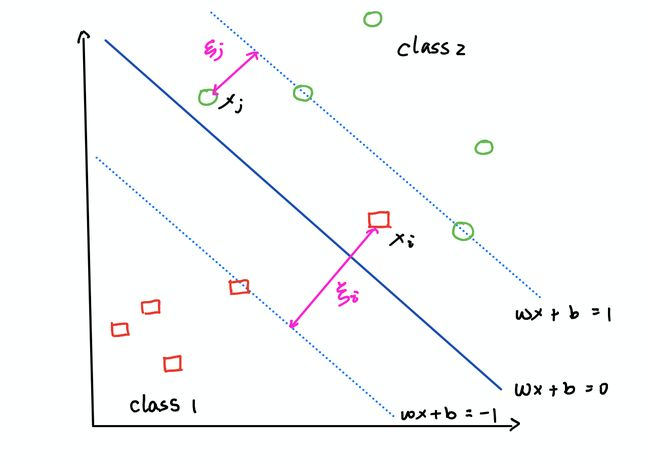
In general, classes are not linearly separable. This may be because the class boundary is not linear, but often there is no clear boundary. To deal with this case, the support vector machine adds a set of “slack variables”, which forgive excursions of a few points into, or even across, the margin, like showing in the graph below:
通常,类不是线性可分离的。 这可能是因为类边界不是线性的,但是通常没有明确的边界。 为了解决这种情况,支持向量机添加了一组“松弛变量”,这些宽恕原谅了到边缘甚至跨越边缘的几个点的偏移,如下图所示:
image by Author 图片作者We want to minimize the total amount of slacks while maximizing the width of the margin, which is called soft-margin support vector machine. This is more widely used, and the objective function becomes:
我们要在使边距的宽度最大的同时,使松弛的总量最小化,这称为软边距支持向量机。 这被更广泛地使用,目标函数变为:
for some constant C. This optimization problem is called the primal problem. The constant C represents the “cost” of the slack. When C is small, it is efficient to allow more points into the margin to achieve a larger margin. Larger C will produce boundaries with fewer support vectors. By increasing the number of support vectors, SVM reduces its variance, since it depends less on any individual observation. Reducing variance makes the model more generalized. Thus, decreasing C will increase the number of support vectors and reduce over-fitting.
对于一些常数C。 此优化问题称为原始问题。 常数C代表松弛的“成本”。 当C较小时,允许有更多点进入边距以实现更大的边距是有效的。 C越大,边界越少,支持向量也越少。 通过增加支持向量的数量,SVM减少了方差,因为它较少依赖于任何单独的观察。 减少方差使模型更通用。 因此,降低C将增加支持向量的数量并减少过度拟合。
With Lagrange multipliers:
使用拉格朗日乘数:
we can rewrite the constrained optimization problem as the primal Lagrangian function :
我们可以将约束优化问题重写为原始拉格朗日函数:
Instead of minimizing over w, b, subject to constraints, we can maximize over the multipliers subject to the relations obtained previously for w, b. This is called the dual Lagrangian formulation:
代替将w , b最小化(受约束),我们可以使乘数最大化,该乘数受先前为w , b获得的关系的约束。 这称为双重拉格朗日公式:
This is now a reasonably straightforward quadratic programming problem, solved with Sequential Minimization Optimization. There are a lot of programming tools you can use to solve the optimizing problem. You can use the CVX tool in Matlab to solve this question. Or if you are familiar with python, you can use the CVXOPT package to solve it. I have another article at Medium that discusses the use of the CVXOPT package, and how to apply it to solve SVM in the dual formulation. Once we have solved this problem for \alpha, we can easily work out the coefficients:
现在这是一个相当简单的二次规划问题,可通过顺序最小化优化解决。 您可以使用许多编程工具来解决优化问题。 您可以使用Matlab中的CVX工具来解决此问题。 或者,如果您熟悉python,则可以使用CVXOPT软件包来解决它。 我在Medium上还有另一篇文章,讨论了CVXOPT软件包的用法,以及如何将其应用于对偶公式中的SVM解决方案。 解决\ alpha的问题后,我们可以轻松计算出系数:
Waling through the math behind the Support Vector Machines algorithm definitely helps understand the implementation of the model. It gives insights on choosing the right model for the right questions and choosing the right value for the hyper-parameters.
仔细阅读支持向量机算法背后的数学知识,无疑有助于理解模型的实现。 它为选择正确的问题模型和为超参数选择正确的值提供了见解。
Hope this helps. Thank you all for reading!
希望这可以帮助。 谢谢大家的阅读!
翻译自: https://towardsdatascience.com/explain-support-vector-machines-in-mathematic-details-c7cc1be9f3b9
支持向量机回归和支持向量机