LDA线性判别分析案例实战

LDA是线性判别分析的简称，该方法是一种线性学习方法，常用于分类。
本文主要思路：
1、二分类LDA原理
2、二分类LDA如何用python实现
3、二分类LDA案例实战
4、多分类LDA原理
5、多分类LDA如何用python实现
6、多分类LDA案例实战

1、二分类LDA原理

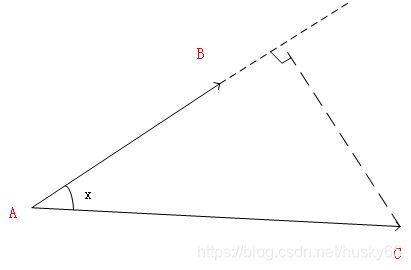
讲解之前先了解一下向量的知识：
如下图所示设向量AB是单位向量，AC是任意向量，向量AC到向量AB的投影为|AC|cosx=ABAC

如下图所示（该图来源于周志华 机器学习的西瓜书，如有侵权，联系删除），对于一个二维空间中的点想（x, y），点（x, y）与原点（0, 0）可以构成一个向量x*。这个向量到图中直线所对应的向量 wT的投影为wT*x。在图中可以看到，这是一个二分类问题，LDA的思想就是将图中的点投影到这条直线上，相同类型的点在直线上的位置会很接近。
但如何让相同类型的点在直线上的投影很接近呢？首先引入方差的概念，方差表示一组数的波动程度，波动程度越大方差越大，如果一组数据在某一个方向上方差很小，那么这组数据在这个方向上的的波动程度也会很小。从下图中可以看出，沿直线垂直的方向上数据的波动程度很小，那么这些数据点投影到这条直线上会挨的很紧密。
LDA是一个有监督的方法，首先通过训练数据求出所要投影的直线，并求出各个类别的中心点center在直线的位置。当需要预测测试数据的类别时，将测试数据也投影到这条直线上。并求出测试数据点到每个类的中心点center的距离，距离哪一个中心点近就是哪一类。

如何求解这条直线呢？下面将会推导：





引用自：https://www.cnblogs.com/hfdkd/articles/7730512.html

通过上述计算最终得到w，求出直线。
（上面推导不止适用于二维空间，同样适用于高维空间）
**

所以LDA具体步骤为：

**
1、根据训练数据求出w；
2、根据w计算出训练数据每一类数据对应中心点M在直线上的投影距离；
3、根据w计算测试数据在直线上的投影距离x，根据投影距离x计算到中心点M的距离,距离那一个中心点近就是哪一类数据。

LDA利用Python编写：

import numpy as np
import pandas as pd
from collections import Counter
import matplotlib.pyplot as plt


class BinaryClassification:
    """
    LDA二分类
    """
    def fit(self, x, y):
        """
        :param x: 训练样本
        :param y: 训练标签
        :return:
        """
        # 将x,y转换为数组，方便接下来计算
        x = np.array(x)
        y = np.array(y)
        # 判断是否为二分类问题
        self.re = Counter(y)
        if len(self.re.keys()) != 2:
            raise ValueError("二分类问题，需要传入两类数据")

        # c1存储第一类数据,c2存储第一类数据
        c1 = []
        c2 = []
        for temp_x, temp_y in zip(x, y):
            if temp_y == list(self.re.keys())[0]:
                c1.append(temp_x)
            else:
                c2.append(temp_x)
        c1 = np.array(c1)
        c2 = np.array(c2)
        # 计算每类的平均值
        mean1 = np.mean(c1, axis=0)
        mean2 = np.mean(c2, axis=0)
        # 计算每类的方差
        var1 = np.var(c1, axis=0)
        var2 = np.var(c2, axis=0)
        # print(mean1, mean2, var1, var2)
        # 计算每类协方差
        cov1 = np.dot(c1.T, c1)/list(self.re.values())[0]
        cov2 = np.dot(c2.T, c2)/list(self.re.values())[1]
        # print(cov1)
        # print(cov2)
        # 计算类内散度矩阵Sw就是上文中的B
        Sw = cov1 + cov2
        # 计算类内散度矩阵Sb就是上文中的A
        sb = np.array(mean2 - mean1)
        Sb = np.dot(sb.reshape([-1, 1]), [sb])
        # 求解瑞利熵的最大值
        U, sigma, VT = np.linalg.svd(np.dot(np.linalg.inv(Sw), Sb))
        w = VT[0]
        # 计算每类样本中心点在超平面（直线）上的位置
        center1 = np.dot(w, mean1.T)
        center2 = np.dot(w, mean2.T)

        return w, center1, center2

    def predict(self, X, w, center1, center2):
        # 计算每个样本值的在超平面上的位置
        X = np.array(X)
        position = np.dot(w, X.T)
        # 计算样本点到各个中心点的距离
        dis1 = np.abs(position - center1)
        dis2 = np.abs(position - center2)
        # 比较样本点到两个中心点的距离的大小，样本属于距离小的点
        compare = dis1 - dis2
        # label用于存储X中数据的类别
        label = []
        for i in compare:
            if i < 0:
                label.append(list(self.re.keys())[0])
            else:
                label.append(list(self.re.keys())[1])

        return label

二分类LDA案例实战：
训练数据如下（A-M表示数据特征，label表示标签，0表示第一类数据，1表示第二类数据）：
| | |

测试数据如下（后七个数据为第二类数据，前面为第一类数据）：
| | |

def main():
    lda = BinaryClassification()
    data = pd.read_excel("二分类数据.xlsx", sheet_name=2)
    data1 = pd.read_excel("二分类数据.xlsx", sheet_name=3)
    x = np.array(data.values)[:, :-1].reshape([-1, 13])
    y = np.array(data.values)[:, -1]
    w, center1, center2 = lda.fit(x, y)
    print(center1)
    print(center2)
    X = np.array(data1.values)
    label = lda.predict(X, w, center1, center2)
    print(label)


if __name__ == "__main__":
    main()

测试结果：

可以看出可以准确的分类。

**

4、多分类LDA

**
上述是二分类LDA，对于多分类LDA常见的方式有OVO（1对1），OVR（1对其它），MvM（多对多），以及用上述公式推导直接求出多分类。
（1）OVO（1对1）
该方法是从训练数据中任意选取两类数据去构建分类器，(假设有N种类别)一共可以构建N(N-1)/2个分类器，运用这些分类器去分类测试样本，每一个测试样本都可以得到N(N-1)/2个结果，对每一个样本选取结果中数量最多的结果作为最终结果。
代码：

from collections import Counter
def ones_vs_ones(x, y, X):
    # 一对一分类
    lda = BinaryClassification()
    count = Counter(y)
    # 计算有多少种类的数据
    label = list(count.keys())
    # print(label)
    num = len(count)
    # 存储每次分类出的类别
    result = []
    for i in range(num - 1):
        sub_label = []
        sub_x = []
        sub_y = []
        for j in np.arange(i+1, num, 1):
            sub_label.append(label[i])
            sub_label.append(label[j])
            for index, temp in enumerate(y):
                if (temp == sub_label[0]) or (temp == sub_label[1]):
                    sub_x.append(x[index])
                    sub_y.append(temp)
            w, center1, center2 = lda.fit(sub_x, sub_y)
            result.append(lda.predict(X, w, center1, center2))
    result = np.array(result)
    # 计算最终结果
    re = []
    for i in range(X.shape[0]):
        re.append(max(Counter(result[:, i])))

    return re

用上面数据测试结果：

data = pd.read_excel("二分类数据.xlsx", sheet_name=2)
data1 = pd.read_excel("二分类数据.xlsx", sheet_name=3)
x = np.array(data.values)[:, :-1].reshape([-1, 13])
y = np.array(data.values)[:, -1]
X = np.array(data1.values)
re = ones_vs_ones(x, y, X)
print(re)

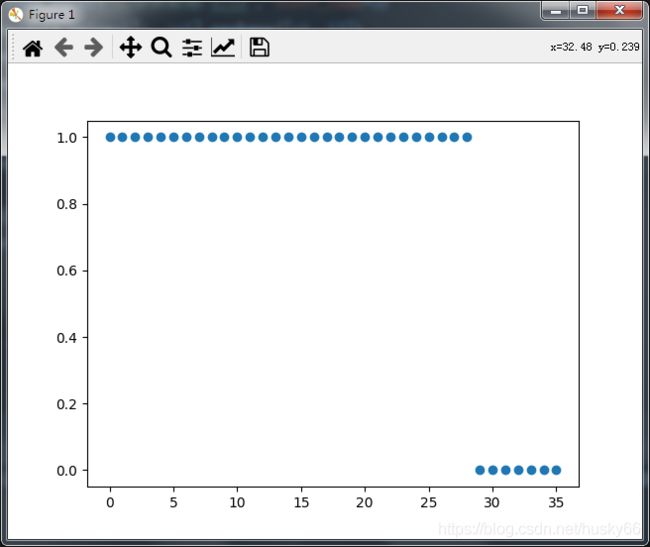
plt.figure()
plt.scatter(list(range(X.shape[0])), re)
plt.show()

[1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]

（2）OvR(一对其余)
一对其余是通过构建N个分类器，来进行分类，每一个分类器是选择一个类别作为正类其它类别作为负类，（例如：有4种类别1,2,3,4；选择其中2作为正类，1,3,4作为一类叫做负类），总共可以构建N个分类器，用测试数据进行测试时，如果测试数据中一个数据点分类为正类那么他就属于这一类。一般情况下，每一个测试数据只有一个正类，其它全为负类，但也有时候有多个负类，这时需要计算每个分类器的置信度，选择置信度大的正类结果作为最终结果。
代码如下：

def ones_vs_others(x, y, X):
    # 一对其余，这里没有计算分类器的置信度
    lda = BinaryClassification()
    count = Counter(y)
    # 计算有多少种类的数据
    label = list(count.keys())
    # 存储每次分类出的类别
    result = []
    for i in label:
        sub_x = np.copy(x)
        sub_y = np.copy(y)
        for index, j in enumerate(y):
            if j != i:
                sub_y[index] = 0
            else:
                sub_y[index] = 1
        w, center1, center2 = lda.fit(sub_x, sub_y)
        result.append(lda.predict(X, w, center1, center2))
    result = np.array(result)

    re = []
    for i in range(X.shape[0]):
        for temp, j in enumerate(result[:, i]):
            if j == 1:
               re.append(label[temp])

    return re

用上面数据分类结果：

data = pd.read_excel("二分类数据.xlsx", sheet_name=2)
data1 = pd.read_excel("二分类数据.xlsx", sheet_name=3)
x = np.array(data.values)[:, :-1].reshape([-1, 13])
y = np.array(data.values)[:, -1]
X = np.array(data1.values)

re = ones_vs_others(x, y, X)

plt.figure()
plt.scatter(list(range(X.shape[0])), re)
plt.show()

未完待续。。。。