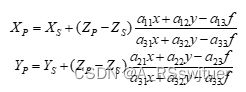C# GDAL 数字图像处理Part8 无人机影像粗校正
好!
今天我们来更新“无人机影像粗校正”的部分。
其实老师刚刚开始布置任务的时候,我一直不明白是什么意思,后来再问了一下才知道,我们到底要干嘛。接下来,细述本次任务的概要与思想:
一、任务概要
如图所示,我们获得了一幅无人机影像图片(影像来源:SWJTU 地院 曹老师):
我们打开自己的软件(前提是你已经做了 显示鼠标所在位置地理坐标 的功能,详见:
C# GDAL 数字图像处理Part4 获得鼠标位置的地理坐标_A_RSswjtuer的博客-CSDN博客)
鼠标移动到上边,我们会发现,该影像的地理坐标(如下图示)是有误的,或者说是并未设置的,那么我们的任务,就是求出且设置它的仿射变换六参数,使得它有正确的地理坐标。
二、解决思路
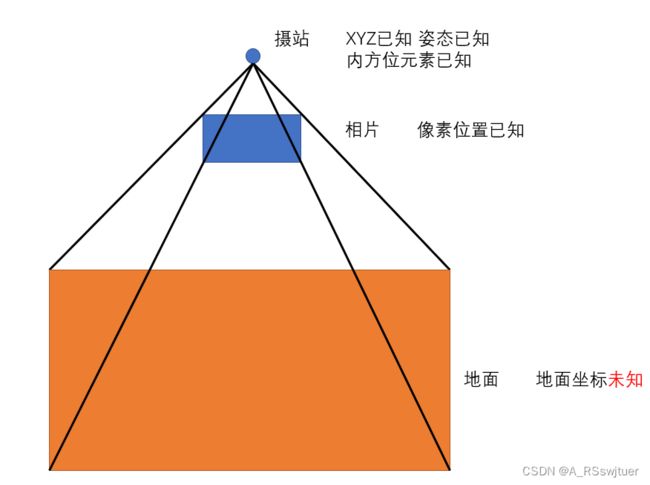
首先,我们回想一下之前学过的《摄影测量学基础》,里面有一个共线方程(来源:百度百科):
我们可以知道,一条直线的共线方程包含以下几个要素:像平面坐标、相机(摄站)的地理坐标、物体的地理坐标 、内方位元素与方向。
那么在拍照的时候,借助POS系统,我们会知道 相机(摄站)的地理坐标 与 方向。
内方位元素、像平面坐标可以通过产品信息获得
所以我们需要根据这四个条件求出像素对应位置的地理坐标。
对于像素位置,我们选用四角的像素位置即可,比较方便。那情况就如下图:
当我们有了像素坐标(x,y)和对应地理坐标(X,Y),想要解求仿射变换六参数,那问题就变得和Part7(C# GDAL 数字图像处理Part7 仿射变换图像配准_A_RSswjtuer的博客-CSDN博客)的求解仿射变换六参数相同了。本文会用到和Part7一样的最小二乘拟合多元一次多项式的类,如果自己并未实现此类,建议先去看Part7。
好,这就是我们要做的事情。
三、代码实现
我们先看四个已知值,像平面坐标、姿态信息、摄站坐标、内方位元素:
3.1 像平面坐标
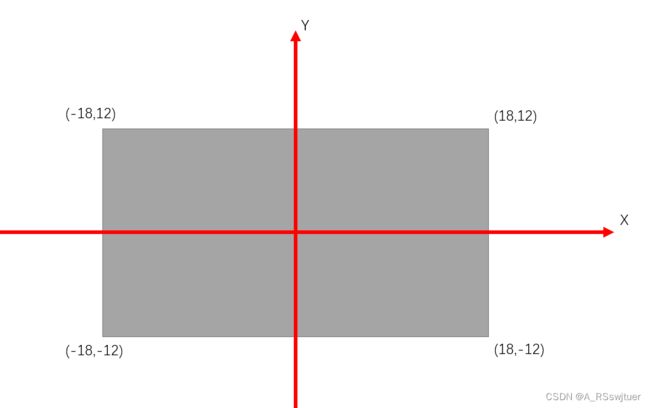
像平面坐标怎么求?其实我们只需要知道相机参数的传感器尺寸即可,听起来复杂其实也就是相片的大小。假如一张相片长为36mm,宽为24mm,那它的四角坐标如下图:
这里是以中心为原点,那么相片的长和宽得让用户输入。
3.2内方位元素
内方位元素x0、y0以及f 都是商家在生产相机时给出的坐标,让用户输入即可。
3.3姿态信息
姿态信息也就是相机在α、β、κ方向上的转角,也是用户输入。
3.4摄站坐标
摄站坐标也就是相机在拍摄时的地理坐标,还是用户输入。
3.5计算公式
首先我们通过以下公式计算a矩阵:
代码是这样:
private double d2h(double d)//度转弧度
{
return d / 180.0 * Math.PI;
}
private void Compute_paras_a()
{
//Paras_a是一个double[3,3]的成员变量
//Phi、Omega、Kappa是用户输入的值
this.Paras_a[0, 0] = Math.Cos(d2h(this.Phi)) * Math.Cos(d2h(this.Kappa)) -
Math.Sin(d2h(this.Phi)) * Math.Sin(d2h(this.Omega)) * Math.Sin(d2h(this.Kappa));
this.Paras_a[0, 1] = (-Math.Cos(d2h(this.Phi))) * Math.Sin(d2h(this.Kappa)) -
Math.Sin(d2h(this.Phi)) * Math.Sin(d2h(this.Omega)) * Math.Cos(d2h(this.Kappa));
this.Paras_a[0, 2] = (-Math.Sin(d2h(this.Phi))) * Math.Cos(d2h(this.Omega));
this.Paras_a[1, 0] = Math.Cos(d2h(this.Omega)) * Math.Sin(d2h(this.Kappa));
this.Paras_a[1, 1] = Math.Cos(d2h(this.Omega)) * Math.Cos(d2h(this.Kappa));
this.Paras_a[1, 2] = (-Math.Sin(d2h(this.Omega)));
this.Paras_a[2, 0] = Math.Sin(d2h(this.Phi)) * Math.Cos(d2h(this.Kappa)) +
Math.Cos(d2h(this.Phi)) * Math.Sin(d2h(this.Omega)) * Math.Sin(d2h(this.Kappa));
this.Paras_a[2, 1] = (-Math.Sin(d2h(this.Phi))) * Math.Sin(d2h(this.Kappa)) +
Math.Cos(d2h(this.Phi)) * Math.Sin(d2h(this.Omega)) * Math.Sin(d2h(this.Kappa));
this.Paras_a[2, 2] = Math.Cos(d2h(this.Phi)) * Math.Cos(d2h(this.Omega));
}接下来呢,我们通过以下公式计算四个角点的地理坐标:
其中 下标为p 是物体地理坐标, 下标为s 是摄站的XYZ坐标。
我们可以看到这里多了一个 Zp ,课上说可以用 成像区域平均高程 替代,这也是需要用户输入的一部分哈~
那么,代码如下:
private void Compute_corners_coor()
{
double[,] xy = new double[4, 2];//计算像平面坐标
xy[0, 0] = -0.5 * this.Camera_W; xy[0, 1] = 0.5 * this.Camera_H; //LT
xy[1, 0] = 0.5 * this.Camera_W; xy[1, 1] = 0.5 * this.Camera_H; //RT
xy[2, 0] = -0.5 * this.Camera_W; xy[2, 1] = -0.5 * this.Camera_H; //LB
xy[3, 0] = 0.5 * this.Camera_W; xy[3, 1] = -0.5 * this.Camera_H; //RB
for (int i = 0;i<4;i++)
{
//Corners_coor的类型是double[4,2],代表四个角点以及每个角点的地理坐标XY
//Area_AvH代表区域平均高程
//Img_H代表的是成像时摄站的高程Z。
//四角坐标的X
this.Corners_coor[i, 0] = this.Camera_XY[0] + (this.Area_AvH - this.Img_H) *
(this.Paras_a[0, 0] * xy[i, 0] + this.Paras_a[0, 1] * xy[i, 1] - this.Paras_a[0, 2] * this.f)
/
(this.Paras_a[2, 0] * xy[i, 0] + this.Paras_a[2, 1] * xy[i, 1] - this.Paras_a[2, 2] * this.f);
//四角坐标的Y
this.Corners_coor[i, 1] = this.Camera_XY[1] + (this.Area_AvH - this.Img_H) *
(this.Paras_a[1, 0] * xy[i, 0] + this.Paras_a[1, 1] * xy[i, 1] - this.Paras_a[1, 2] * this.f)
/
(this.Paras_a[2, 0] * xy[i, 0] + this.Paras_a[2, 1] * xy[i, 1] - this.Paras_a[2, 2] * this.f);
}//计算出了四角坐标
}这样,我们就计算出来了四角的地理坐标。
现在,我们有四组像素坐标(注意,这里变为像素坐标,从(0,0)开始!之前的是像片坐标),四组地理坐标,就可以参照仿射变换的公式,使用之前说到的类进行最小二乘拟合求解最佳参数。(P7有说过类怎么使用,这里就不多赘述)
最后,我们就求出新的六参数了:{a,b,c,d,e,f}
但是这还不能设置到图像中。
在我的Part4:(C# GDAL 数字图像处理Part4 获得鼠标位置的地理坐标_A_RSswjtuer的博客-CSDN博客)中有提到地理坐标的计算公式是:
GeoX = argout[0] + argout[1] * x + argout[2] * y
GeoY = argout[3] + argout[4] * x + argout[5] * y
可以看到,第一项是常数项,第二三项才是乘以xy的参数ab,所以我们应该对原始的六参数顺序进行变换,使得常数项在前:
{a, b, c, d, e, f} --> {c, a, b, f, d, e}
好,这样就完成了我们仿射变换六参数的计算!
3.6为Dataset设置仿射变换六参数
其实很简单,假设我们输出的Dataset名字是“output_dataset",我们使用:
output_dataset . SetGeoTransform(六参数double数组)
即可。
注意,输入的数组一定要是double[6]。
好,今天的更新就到这里!