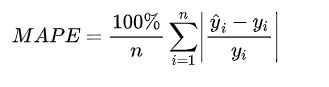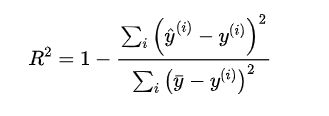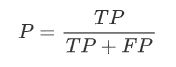深度学习(18)机器学习常用的评价指标
评价指标
- 回归问题
-
- 1. MAE:平均绝对误差(Mean Absolute Error)
- 2. MSE:均方误差(Mean Square Error)
- 3. RMSE:根均方误差(Root Mean Square Error)
- 4. MAPE:平均绝对百分比误差(Mean Absolute Percentage Error)
- 5. SMAPE:对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error)
- 6. R Squared:
- 7. 代码实现:
- 分类问题
-
- 0. Confusion Matrix(混淆矩阵):
- 1. Accuracy(准确率):
- 2. Precision(精准率):
- 3. Recall(召回率):
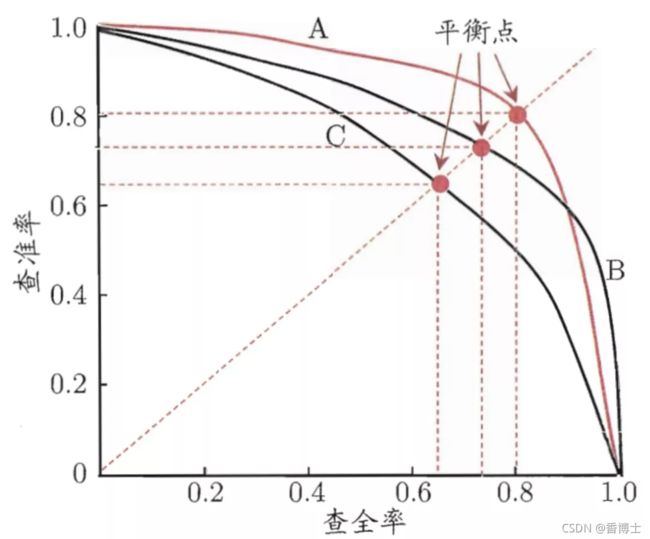
- 4. P-R曲线:
- 5. (加权调和平均)和 (调和平均):
- 6. ROC-AUC:
- 7. 代码实现:
- 参考资料:
如何评估机器学习算法模型是任何项目中一个非常重要的环节。分类问题一般会选择准确率(Accuracy)或者AUC作为metric,回归问题使用MSE,但这些指标并不足以评判一个模型的好坏,接下来的内容我将尽可能包括各个评价指标。因为损失函数大部分可以直接作为评价指标,所以损失函数中出现过的简单介绍。
回归问题
1. MAE:平均绝对误差(Mean Absolute Error)
2. MSE:均方误差(Mean Square Error)
3. RMSE:根均方误差(Root Mean Square Error)
取均方误差的平方根可以使得量纲一致,这对于描述和表示是有意义的。
4. MAPE:平均绝对百分比误差(Mean Absolute Percentage Error)
注意点:当真实值有数据等于0时,存在分母0除问题,该公式不可用!
5. SMAPE:对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error)
注意点:真实值、预测值均等于0时,存在分母为0,该公式不可用!
6. R Squared:
即决定系数(Coefficient of determination),被人们称为最好的衡量线性回归法的指标。
如果我们使用同一个算法模型,解决不同的问题,由于不同的数据集的量纲不同,MSE、RMSE等指标不能体现此模型针对不同问题所表现的优劣,也就无法判断模型更适合预测哪个问题。得到的性能度量都在[0, 1]之间,可以判断此模型更适合预测哪个问题。
公式的理解:
分母代表baseline(平均值)的误差,分子代表模型的预测结果产生的误差;
预测结果越大越好,为1说明完美拟合,为0说明和baseline一致;
7. 代码实现:
# coding=utf-8
import numpy as np
from sklearn import metrics
from sklearn.metrics import r2_score
# MAPE和SMAPE需要自己实现
def mape(y_true, y_pred):
return np.mean(np.abs((y_pred - y_true) / y_true)) * 100
def smape(y_true, y_pred):
return 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])
# MSE
print(metrics.mean_squared_error(y_true, y_pred)) # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred))) # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred)) # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred)) # 76.07142857142858
# SMAPE
print(smape(y_true, y_pred)) # 57.76942355889724
# R Squared
print(r2_score(y_true, y_pred))
分类问题
0. Confusion Matrix(混淆矩阵):
混淆矩阵一般不直接作为模型的评价指标,但是他是后续多个指标的基础。以下为二分类的混淆矩阵,多分类的混淆矩阵和这个类似。

我们训练模型的目的是为了降低FP和FN。很难说什么时候降低FP,什么时候降低FN。基于我们不同的需求,来决定降低FP还是FN。
-
降低假负数例(FN):假设在一个癌症检测问题中,每100个人中就有5个人患有癌症。在这种情况下,即使是一个非常差的模型也可以为我们提供95%的准确度。但是,为了捕获所有癌症病例,当一个人实际上没有患癌症时,我们可能最终将其归类为癌症。因为它比不识别为癌症患者的危险要小,因为我们可以进一步检查。但是,错过癌症患者将是一个巨大的错误,因为不会对其进行进一步检查。
-
降低假正例(FP):假设在垃圾邮件分类任务中,垃圾邮件为正样本。如果我们收到一个正常的邮件,比如某个公司或学校的offer,模型却识别为垃圾邮件(FP),那将损失非常大。所以在这种任务中,需要尽可能降低假正例。
1. Accuracy(准确率):
当样本类别均衡时,Accuracy是一个很好的指标。
但在样本不平衡的情况下,产生效果较差。假设我们的训练数据中只有2%的正样本,98%的负样本,那么如果模型全部预测为负样本,准确率便是98%,。分类的准确率指标很高,会给我们一种模型很好的假象。
2. Precision(精准率):
含义:预测为正例的样本中有多少实际为正;
3. Recall(召回率):
4. P-R曲线:
通过选择不同的阈值,得到Recall和Precision,以Recall为横坐标,Precision为纵坐标得到的曲线图。
- PR曲线性质:
- 如果一个学习器的P-R曲线被另一个学习器的曲线完全包住,后者性能优于前者;
- 如果两个学习器的曲线相交,可以通过平衡点(如上图所示)来度量性能;
- 阈值下降:
- Recall:不断增加,因为越来越多的样本被划分为正例,假设阈值为0.,全都划分为正样本了,此时recall为1;
- Precision:正例被判为正例的变多,但负例被判为正例的也变多了,因此precision会振荡下降,不是严格递减;
- 如果有个划分点可以把正负样本完全区分开,那么P-R曲线面积是1*1;
5. (加权调和平均)和 (调和平均):
6. ROC-AUC:
Area Under Curve(AUC) 是二分类问题中使用非常广泛的一个评价指标。AUC的本质是,任取一个正样本和负样本,模型输出正样本的值大于负样本值的概率。构成AUC的两个基本指标是假正例率和真正例率。

TPR和FPR的范围均是[0,1],通过选择不同的阈值得到TPR和FPR,然后绘制ROC曲线。

- 曲线性质:
阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1);
ROC曲线越靠近左上角,该分类器的性能越好;
对角线表示一个随机猜测分类器;
若一个学习器的ROC曲线被另一个学习器的曲线完全包住,后者性能优于前者;
AUC: ROC曲线下的面积为AUC值。
7. 代码实现:
from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score,fbeta_score
y_test = [1,1,1,1,0,0,1,1,1,0,0]
y_pred = [1,1,1,0,1,1,0,1,1,1,0]
print("准确率为:{0:%}".format(accuracy_score(y_test, y_pred)))
print("精确率为:{0:%}".format(precision_score(y_test, y_pred)))
print("召回率为:{0:%}".format(recall_score(y_test, y_pred)))
print("F1分数为:{0:%}".format(f1_score(y_test, y_pred)))
print("Fbeta为:{0:%}".format(fbeta_score(y_test, y_pred,beta =1.2)))
参考资料:
[1]分类问题性能评价指标详述:
https://blog.csdn.net/foneone/article/details/88920256
[2]AUC,ROC我看到的最透彻的讲解:
https://blog.csdn.net/u013385925/article/details/80385873
[3]机器学习大牛最常用的5个回归损失函数,你知道几个?:
https://www.jiqizhixin.com/articles/2018-06-21-3
[4]机器学习-损失函数:
https://www.csuldw.com/2016/03/26/2016-03-26-loss-function/
[5]损失函数jupyter notebook:
https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/05_Loss_Functions.ipynb
[6]L1 vs. L2 Loss function:
http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
[7]P-R曲线深入理解:
https://blog.csdn.net/b876144622/article/details/80009867