【ELM预测】麻雀算法优化极限学习机预测（含前后对比）【含Matlab源码 2202期】

⛄一、麻雀搜索算法优化深度学习极限学习机DELM预测模型实现流程

1 麻雀搜索算法
麻雀搜索算法是一种新型的群智能优化算法，在2020年由Xue等提出，主要是受麻雀的觅食和反哺食行为启发，具有寻优能力强、收敛速度快的特点。

麻雀搜索算法将整个麻雀种群分为三类，即寻找食物的生产者，抢夺食物的加入者和发现危险的警戒者。生产者和加入者可以相互转化，但各自在种群中的占比不会发生变化。

在模拟实验中，需要使用虚拟麻雀进行食物的寻找，与其他寻优算法相同，麻雀搜索算法首先需要对麻雀种群与适应度值进行初始化，麻雀种群可初始化为如下形式，表达式为

式(3)中：n为麻雀的数量；d为要优化的变量的维度即独立参数的数目；xn,d为第n只麻雀第d维度的值。

由此，总体麻雀适应度值表征形式为

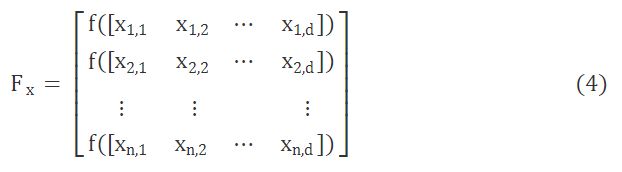
式(4)中：f(x)为个体适应度值。适应度值较好的麻雀(即生产者)在搜索中会优先获得食物并指引群体的觅食方向与范围，与此同时，生产者会具有更大的觅食搜索范围。

生产者在觅食过程中，位置不断发生移动，而在遇到捕食者时，移动规则又会发生改变，即

式(5)中：t为当前迭代次数；j∈{1,2,…,d};xti,j为迭代第t次时，第i个麻雀的第j个维度的值；α∈(0,1],为随机数；itermax 为迭代次数最多的常数；R2∈[0,1],为报警值；ST∈[0,1],为安全阈值；Q为服从正态分布的随机数；L为1×d阶矩阵(元素全为1)。R2

而对加入者而言，在觅食过程中，一旦生产者找到了好的食物源，加入者必会知晓，并飞向它的附近抢食，同时，也有加入者会时刻监视生产者，随时准备争抢食物。由此加入者的位置更新规则为

式(6)中：xp为生产者占据的最佳位置；xworst为全局最差位置；A为1×d阶矩阵，每个元素随机为1或-1;A†=AT(AAT)-1。当i>n2时，表示适应性较差的第i个加入者抢夺食物失败，为了更好地获得食物避免挨饿只能飞往其他地区进行觅食。

总体而言，假设意识到危险的麻雀(即警戒者)占10%～20%。初始位置则随机产生，规则为

式(7)中：λ为步长控制函数，是一个均值为0,方差为1的正态分布随机数；fi为当前麻雀适应值；fg为全局最好适应值；fw为全局最差适应值；k为麻雀移动方向；xbest为全局最优位置；ε为最小常数，避免除数为零。当fi>fg时，警戒者位于种群边缘，意识到危险后向中央安全区靠近；当fi=fg时，则是处于种群中央的麻雀意识到了危险，为躲避危险，则向其他麻雀身边靠拢。

⛄二、部分源代码

%% 初始化
clear
close all
clc
format shortg
warning off
addpath(‘func_defined’)

%% 读取读取
data=xlsread(‘数据.xlsx’,‘Sheet1’,‘A1:N252’); %%使用xlsread函数读取EXCEL中对应范围的数据即可

%输入输出数据
input=data(:,1:end-1); %data的第一列-倒数第二列为特征指标
output=data(:,end); %data的最后面一列为输出的指标值

N=length(output); %全部样本数目
testNum=15; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目

%% 划分训练集、测试集
input_train = input(1:trainNum,:)‘;
output_train =output(1:trainNum)’;
input_test =input(trainNum+1:trainNum+testNum,:)‘;
output_test =output(trainNum+1:trainNum+testNum)’;

%% 数据归一化
[inputn,inputps]=mapminmax(input_train,-1,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax(‘apply’,input_test,inputps);

%% 获取输入层节点、输出层节点个数
inputnum=size(input,2);
outputnum=size(output,2);
disp(‘/’)
disp(‘极限学习机ELM结构…’)
disp([‘输入层的节点数为：’,num2str(inputnum)])
disp([‘输出层的节点数为：’,num2str(outputnum)])
disp(’ ')
disp(‘隐含层节点的确定过程…’)

%确定隐含层节点个数
%注意：BP神经网络确定隐含层节点的方法是：采用经验公式hiddennum=sqrt(m+n)+a，m为输入层节点个数，n为输出层节点个数，a一般取为1-10之间的整数
%在极限学习机中，该经验公式往往会失效，设置较大的范围进行隐含层节点数目的确定即可。

MSE=1e+5; %初始化最小误差
for hiddennum=20:30

%用训练数据训练极限学习机模型

[IW0,B0,LW0,TF,TYPE] = elmtrain(inputn,outputn,hiddennum);

%对训练集仿真
an0=elmpredict(inputn,IW0,B0,LW0,TF,TYPE);  %仿真结果
mse0=mse(outputn,an0);  %仿真的均方误差
disp(['隐含层节点数为',num2str(hiddennum),'时，训练集的均方误差为：',num2str(mse0)])

%% 训练最佳隐含层节点的极限学习机模型
disp(’ ')
disp(‘ELM极限学习机：’)
[IW0,B0,LW0,TF,TYPE] = elmtrain(inputn,outputn,hiddennum_best);

%% 麻雀搜索算法寻最优权值阈值
disp(’ ')
disp(‘SSA优化ELM极限学习机：’)
%初始化SSA参数
N=30; %初始种群规模
M=100; %最大进化代数
dim=inputnumhiddennum_best+hiddennum_best; %自变量个数
%自变量下限
lb=[-ones(1,inputnumhiddennum_best) … %输入层到隐含层的连接权值范围是[-1 1] 下限为-1
zeros(1,hiddennum_best)]; %隐含层阈值范围是[0 1] 下限为0
%自变量上限
ub=ones(1,dim);
[Convergence_curve,bestX]=SSA(N, dim, ub, lb,M,hiddennum_best, inputn, outputn, output_train, inputn_test ,outputps, output_test);
%% 绘制进化曲线
figure
plot(Convergence_curve,‘r-’,‘linewidth’,2)
xlabel(‘进化代数’)
ylabel(‘均方误差’)
legend(‘最佳适应度’)
title(‘SSA的进化曲线’)

%% 作图
figure
plot(output_test,‘b-.o’,‘linewidth’,2)
hold on
plot(test_simu0,‘g-s’,‘linewidth’,2)
hold on
plot(test_simu1,‘r-p’,‘linewidth’,2)
legend(‘真实值’,‘ELM预测值’,‘SSA-ELM预测值’)
xlabel(‘测试样本编号’)
ylabel(‘指标值’)
title(‘优化前后的ELM模型预测值和真实值对比图’)

figure
plot(error0,‘b-s’,‘markerfacecolor’,‘g’)
hold on
plot(error1,‘r-p’,‘markerfacecolor’,‘g’)
legend(‘ELM预测误差’,‘SSA-ELM预测误差’)
xlabel(‘测试样本编号’)
ylabel(‘预测偏差’)
title(‘优化前后的ELM模型预测值和真实值误差对比图’)

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]马飞燕,李向新.基于改进麻雀搜索算法-核极限学习机耦合算法的滑坡位移预测模型[J].科学技术与工程. 2022,22(05)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除