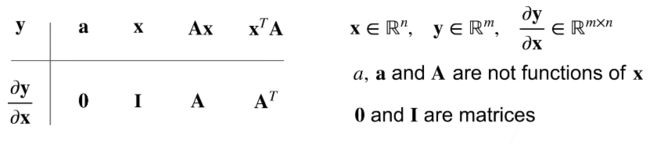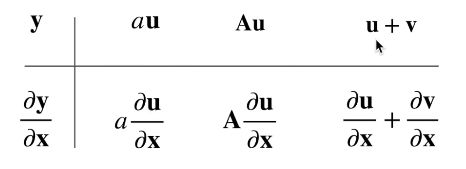深度学习笔记

根据B站李沐大神动手深度学习课程记录
初学者多有不足，欢迎大佬指正

1. 图片分类
2. 物体检测和分割
3. 样式迁移
4. 人脸合成
5. 文字生成图片
6. 文字生成
7. 无人驾驶

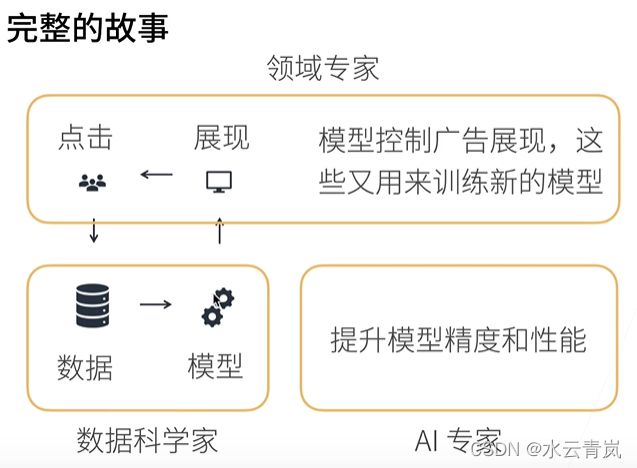
案例 广告点击

• 触发，输入搜索
• 点击率预测，机器学习
• 对广告排序

特征提取，模型预测 根据用户已有的点击数据，进行模型训练

1. 数据操作

1. 创建数组

   1. 形状，例如3*4矩阵
   2. 元素类型
   3. 元素值

2. 访问元素

   [起始（含）:终止（不含）:步长]

2. 数据操作实现

测试

import torch
#创建一维向量
x = torch.arrange(12)
X = x.reshape(3,4)
#reshape不必指定所有维度，参数-1会自动计算对应维度，
#即x.reshape(-1, 4),x.reshape(3,-1)与上等同

#查看张量tensor形状，大小，维数
x.shape
x.numal
x.dim
#用0，1，随机数，创建指定形状的张量
torch.zeros(形状)
torch.ones(形状)
torch.randn(形状)
#创建指定数值的张量
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
#+ - * / **(乘方)按元素运算
torch.exp(x)#将张量x中的个元素用e的x次方代替
x.sum()#求和
x.T#转置
y = x.clone()
x == y#创建一个bool张量

#合成
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X, Y), dim=0), torch.cat((X, Y), dim=1)#0维按行，1维按列

#广播机制
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
(tensor([[0],
         [1],
         [2]]),
 tensor([[0, 1]]))
 #先复制
 (tensor([[0, 0],
         [1, 1],
         [2, 2]]),
 (tensor([[0, 0],
         [1, 1],
         [2, 2]])
#再求和
tensor([[0, 1],
        [1, 2],
        [2, 3]])

#索引
x[-1]#最后1列
x[1:3]#第2，3行
x[1, 2] = 9#更改指定元素
x[0:2, :] = 12#批量更改元素，1，2行

#内存
#X[:] = X + Y或X += Y是在原有内存上更改
#Y = Y + X则先计算X+Y为结果分配新内存，再将Y指向Y，即id(Y)改变了

#类型转换
A = X.numpy()
B = torch.tensor(A)
type(A), type(B)#查看类型，

a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
(tensor([3.5000]), 3.5, 3.5, 3)

3. 数据预处理

基本思想

1. 删除有缺值的行

2. 用该列的均值代替
   inputs = inputs.fillna(inputs.mean())//用均值代替缺失值

3. 转换为张量，有缺值的转换为0，1另成1列
   inputs = pd.get_dummies(inputs, dummy_na=True)
   NumRooms Alley_Pave Alley_nan
   0 3.0 1 0
   1 2.0 0 1
   2 4.0 0 1
   3 3.0 0 1

import torch
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)

4.线性代数

1. 一般认为列向量是向量的默认方向

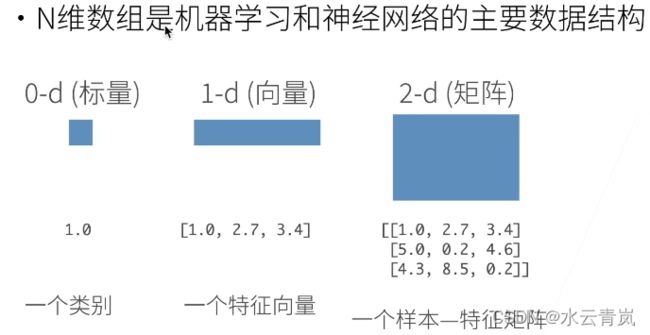
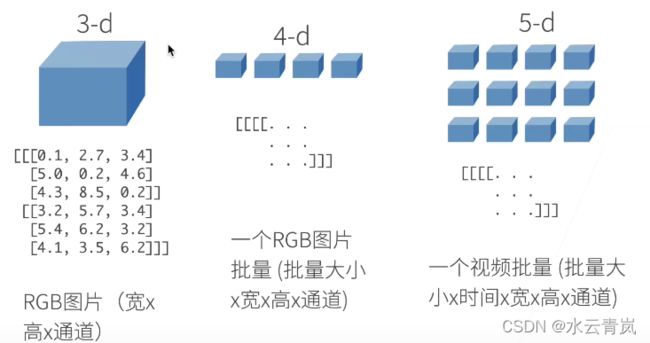
2. 维度（dimension）
   向量或轴的维度被用来表示向量或轴的长度，即向量或轴的元素数量。 然而，张量的维度用来表示张量具有的轴数。 在这个意义上，张量的某个轴的维数就是这个轴的长度。

3. 两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号 ⊙ ）

4. 将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

5. 降维

1. 降维求和

   import torch
   
   x = torch.arange(4, dtype=torch.float32)
   x, x.sum()
   #输出结果
   #tensor([0., 1., 2., 3.]), tensor(6.)
   
   A = torch.arange(20).reshape((5,4))
   A.shape, A.sum()
   (torch.Size([5, 4]), tensor(190.))
   
   #5行4列
   #指定axis=0将通过汇总所有列的元素降维（轴0）。因此，输入轴0的维数在输出形状中消失。
   #按0维求和，即按列求和，0维消失，只剩行维度，1行
   A_sum_axis0 = A.sum(axis=0)
   A_sum_axis0, A_sum_axis0.shape
   (tensor([40., 45., 50., 55.]), torch.Size([4]))
   
   #指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输入轴1的维数在输出形状中消失。
   #按1维求和，即按行求和，1维消失，只剩列维度，1列
   A_sum_axis1 = A.sum(axis=1)
   A_sum_axis1, A_sum_axis1.shape
   (tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))
   

2. 降维求均值

```python
A.mean(), A.sum() / A.numel()#或A.average()
(tensor(9.5000), tensor(9.5000))
  
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
(tensor([ 8.,  9., 10., 11.]), tensor([ 8.,  9., 10., 11.]))
```
3. 非降维
```python
sum_A = A.sum(axis=1, keepdims=True)
sum_A, sum_A.shape
#结果，5行1列的2维张量
tensor([[ 6.],
    	[22.],
    	[38.],
    	[54.],
    	[70.]]), (5, 1)
    	
A / sum_A
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
	    [0.1818, 0.2273, 0.2727, 0.3182],
        [0.2105, 0.2368, 0.2632, 0.2895],
		[0.2222, 0.2407, 0.2593, 0.2778],
		[0.2286, 0.2429, 0.2571, 0.2714]])

如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），我们可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

A.cumsum(axis=0)
#按0维，即按列计算元素的累加总和
tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  6.,  8., 10.],
        [12., 15., 18., 21.],
        [24., 28., 32., 36.],
        [40., 45., 50., 55.]])

6. 矩阵乘法，点积

   np.dot(A, B)

7. 范数
   

   u = np.array([3, -4])
   np.linalg.norm(u)#L2范数
   np.abs(u).sum()#L1范数
   np.linalg.norm(np.ones((4, 9)))#矩阵的Frobenius范数
   

5. 矩阵求导

梯度指向线性变化最大的方向，

梯度即各维度的偏导向量加和

即各维度自变量导数组成的向量

6. 自动求导

import torch

x = torch.arange(4.0, requires_grad=True)
#x.requires_grad_(True)#x.grad存储梯度

y = 2*torch.dot(x, x)
y.backward()#反向传播函数,自动计算y关于x每个分量的梯度
x.grad
#结果 tensor([ 0.,  4.,  8., 12.])
#y=2XTX y`=4X

# 在默认情况下，PyTorch会累积梯度，我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
#tensor([1., 1., 1., 1.])

#分离部分计算图
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x

z.sum().backward()
x.grad == u

#tensor([True, True, True, True])

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x

#tensor([True, True, True, True])

7. 线性回归

1. 线性回归是n维输入的加权，外加偏差

   输入包含d个特征时，我们将预测结果$\hat{y}$（通常使用“尖角”符号表示yy的估计值）表示为：
   $$\hat{y}=w_1{x}_1+...+w_d{x}_d+b.$$
   所有特征放到向量$\mathbf{x}\in {\mathbb{R}}^d$中， 并将所有权重放到向量$\mathbf{w}\in {\mathbb{R}}^d$中， 我们可以用点积形式来简洁地表达模型：
   $$\hat{y}={\mathbf{w}}^{\top }\mathbf{x}+b.$$
   向量$\mathbf{x}$对应于单个数据样本的特征。 用符号表示的矩阵$\mathbf{X}\in {\mathbb{R}}^{n\times d}$可以很方便地引用我们整个数据集的$n$个样本。 其中，$\mathbf{X}$的每一行是一个样本，每一列是一种特征。

   对于特征集合$\mathbf{X}$，预测值$\hat{\mathbf{y}}\in {\mathbb{R}}^n$可以通过矩阵-向量乘法表示为：
   $$\hat{\mathbf{y}}=\mathbf{X}\mathbf{w}+b$$
   给定训练数据特征$\mathbf{X}$和对应的已知标签$\hat{y}$， 线性回归的目标是找到一组权重向量$\mathbf{w}$和偏置$b$： 当给定从$\mathbf{X}$的同分布中取样的新样本特征时， 这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。

2. 用平方损失衡量预测值和真实值的偏差

   通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。 回归问题中最常用的损失函数是平方误差函数。 当样本$i$的预测值为${\hat{y}}^{(i)}$，其相应的真实标签为$y^{(i)}$时， 平方误差可以定义为以下公式：
   $$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2.$$
   为了度量模型在整个数据集上的质量，我们需计算在训练集$n$个样本上的损失均值（也等价于求和）。
   $$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$
   在训练模型时，我们希望寻找一组参数$({\mathbf{w}}^{\ast },b^{\ast })$， 这组参数能最小化在所有训练样本上的总损失。
   $${\mathbf{w}}^{\ast },b^{\ast }=*{argmin}_{\mathbf{w},b}L(\mathbf{w},b).$$

3. 线性回归有显式解

   线性回归的解可以用一个公式简单地表达出来， 这类解叫作解析解（analytical solution）

4. 线性回归可看作单层神经网络

基础优化算法

* 梯度下降即不断沿着反梯度方向更新参数，最小化训练损失
* 小批量随机梯度下降
* 2个超参数，批量大小b，学习率

每次循环时，随机抽取一个固定数量的训练样本，即一个小批量$\mathcal{B}$，计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。将梯度乘以一个预先确定的正数$\eta$（学习率），并从当前参数的值中减掉。

$|\mathcal{B}|$表示每个小批量中的样本数，这也称为批量大小

$\partial$称为偏导数，每次更新都是损失函数对$\mathbf{w}$,$b$分别求偏导，再乘$\eta$相减
$$(\mathbf{w},b)\leftarrow (\mathbf{w},b)-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_{(\mathbf{w},b)}{l}^{(i)}(\mathbf{w},b).$$

8. softmax回归

1. 预测与分类

回归可以用于预测多少的问题。

• 比如预测房屋被售出价格
• 棒球队可能获得的胜场数
• 患者住院的天数

分类问题：不是问“多少”，而是问“哪一个”：

• 某个电子邮件是否属于垃圾邮件文件夹？
• 某个用户可能注册或不注册订阅服务？
• 某个图像描绘的是驴、狗、猫、还是鸡？
• 某人接下来最有可能看哪部电影？

1. 我们只对样本的“硬性”类别感兴趣，即属于哪个类别；
2. 我们希望得到“软性”类别，即得到属于每个类别的概率。
   两者的界限往往很模糊，其中一个原因是：即使我们只关心硬类别，我们仍然使用软类别的模型。

2. 分类标签的表示

独热编码（one-hot encoding）。

独热编码是一个向量，它的分量和类别一样多。 类别对应的分量设置为1，其他所有分量设置为0。

例，标签 y 将是一个三维向量， 其中 (1,0,0) 对应于“猫”、 (0,1,0) 对应于“鸡”、 (0,0,1) 对应于“狗”：
$$y\in \{(1,0,0),(0,1,0),(0,0,1)\}.$$

3. softmax网络架构

为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。

为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数（affine function）。 每个输出对应于它自己的仿射函数。

例，4个特征和3个可能的输出类别
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲\begin{aligned}…

由于计算每个输出$o_1$、$o_2$和$o_3$取决于 所有输入$x_1$、$x_2$、$x_3$和$x_4$， 所以softmax回归的输出层也是全连接层。
$$\mathbf{o}=\mathbf{W}\mathbf{x}+\mathbf{b}$$

4. softmax运算

由于未规范化的预测$\mathbf{o}$可能含有负值，且和不一定为1，不能作为概率

softmax函数将未规范化的预测变换为非负并且总和为1，同时要求模型保持可导。
$$\hat{\mathbf{y}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\mathbf{o})\text{其中}{\hat{y}}_j=\frac{\exp (o_j)}{{\sum }_k\exp (o_k)}$$
softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。 因此，softmax回归是一个线性模型（linear model）。

仿射变换的特点是通过加权和对特征进行线性变换（linear transformation）， 并通过偏置项来进行平移（translation）。

5. 小批量样本的矢量化

假设我们读取了一个批量的样本$\mathbf{X}$， 其中特征维度（输入数量）为$\mathbf{d}$，批量大小为$\mathbf{n}$，在输出中有$\mathbf{q}$个类别。

有小批量特征$\mathbf{X}\in {\mathbb{R}}^{n\times d}$，权重$\mathbf{w}\in {\mathbb{R}}^{d\times q}$，偏置（偏移量）$\mathbf{b}\in {\mathbb{R}}^{1\times q}$
$$\begin{array}{rl}\mathbf{O}& =\mathbf{X}\mathbf{W}+\mathbf{b},\\ \hat{\mathbf{Y}}& =\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\mathbf{O}).\end{array}$$

6. 似然估计

softmax函数给出了一个向量$\hat{\mathbf{y}}$， 我们可以将其视为“对给定任意输入$\mathbf{x}$的每个类的条件概率”

即$\widehat{y_1}=P(y=\text{猫}\mid \mathbf{x})$

假设整个数据集$\{\mathbf{X},\mathbf{Y}\}$具有$n$个样本， 其中索引$i$的样本由特征向量$x^{(i)}$和独热标签向量$y^{(i)}$组成。

其中$x^{(i)}\in {\mathbb{R}}^{d\times 1}$是$d$行1列的列向量，$y^{(i)}\in {\mathbb{R}}^{d\times 1}$是$d$行1列的列向量

$$\begin{gathered} {\mathbf{o}}_{\mathbf{i}}=\mathbf{W}{\mathbf{x}}_{\mathbf{i}}+\mathbf{b} \\ \widehat{{\mathbf{y}}_{\mathbf{i}}}=softmax({\mathbf{o}}_{\mathbf{i}}) \end{gathered}$$

最大似然估计，在样本$\mathbf{X}$下，输出为$\mathbf{Y}$的概率
$$P(\mathbf{Y}\mid \mathbf{X})=\prod _{i=1}^{n}P({\mathbf{y}}^{(i)}\mid {\mathbf{x}}^{(i)}).$$
根据最大似然估计，我们最大化$P(\mathbf{Y} \mid \mathbf{X}) $，相当于最小化负对数似然：
$$-\log P(\mathbf{Y}\mid \mathbf{X})=\sum _{i=1}^n-\log P({\mathbf{y}}^{(i)}\mid {\mathbf{x}}^{(i)})=\sum _{i=1}^{n}l({\mathbf{y}}^{(i)},{\hat{\mathbf{y}}}^{(i)}),$$
其中，对于任何标签$\mathbf{y}$和模型预测$\hat{\mathbf{y}}$，损失函数为：
$$l(\mathbf{y},\hat{\mathbf{y}})=-\sum _{j=1}^q{y}_j\log {\hat{y}}_j.$$

7. 损失函数的导数

对$l(\mathbf{y},\hat{\mathbf{y}})$考虑相对于任何未规范化的预测${\mathbf{o}}_{\mathbf{j}}$的导数，我们得到：
$${\partial }_{o_j}l(\mathbf{y},\hat{\mathbf{y}})=\frac{\exp (o_j)}{{\sum }_{k=1}^q\exp (o_k)}-y_j=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\mathbf{o}{)}_j-y_j.$$
导数是我们softmax模型分配的概率与实际发生的情况（由独热标签向量表示）之间的差异。

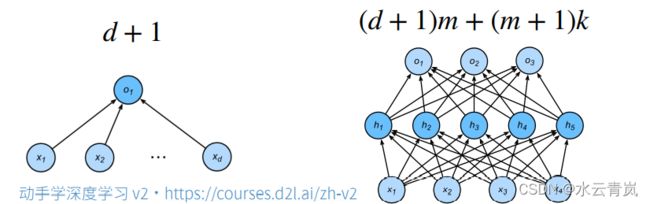
9. 多层感知机MLP

多层感知机使用隐藏层和激活函数得到非线性模型

​ 通过在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。、

在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）$\sigma$。 激活函数的输出（例如，$\sigma (\cdot )$）被称为活性值
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲\begin{aligned}…
多层感知机

${\mathbf{H}}^{(1)}={\sigma }_1(\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)})$

${\mathbf{H}}^{(2)}={\sigma }_2({\mathbf{H}}^{(1)}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)})$

常用激活函数有Sigmoid,Tanh,ReLu

$$\mathrm{ReLU}(x)=\max (x,0).$$

$$\mathrm{pReLU}(x)=\max (0,x)+\alpha \min (0,x).$$

$$\mathrm{sigmoid}(x)=\frac{1}{1+\exp (-x)}.$$

$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}.$$

• 使用Softmax来处理多类分类
• 超参数为隐藏层数，隐藏层大小

10. 模型选择、欠拟合和过拟合

1. 误差

• 训练误差：在训练数据上的误差

• 泛化误差：在新数据上的误差

  • 模考与高考

• 验证数据集：用来评估模型好坏的数据集

  • 不与训练数据混合

• 测试数据集：只用一次的数据集

  • 房子的成交价
  • 未来的考试

• K-则正交检验

  • 在没有足够多数据时使用
  • 算法：
    • 将训练数据分成k块
    • for(i = 1,……，k)
      • 用第$i$块作为验证数据集，其余$(k-1)$块作训练数据集
    • 误差取$k$个验证集误差的均值

• 训练数据集：训练模型参数

• 验证数据集：选择模型超参数

• 非大数据集常用k-折交叉验证

2. 过拟合与欠拟合

	简单	复杂
低	正常	欠拟合
高	过拟合	正常

• 模型容量：影响拟合各种函数的能力
• 低容量的模型难以拟合训练数据
• 高容量的模型可以记住所有的训练数据
  

3. 估计模型容量

• 难以在不同的种类算法之间比较

• 给定一个模型种类

  • 参数的个数

  • 参数值的选择范围

• VC维

4. 数据复杂度

• 样本个数

• 每个样本的元素个数

• 时间、空间结构

• 多样性

5. 总结

• 模型容量需要与数据复杂度相匹配，否则可能造成欠拟合或过拟合
• 统计机器学习提供数学工具衡量模型复杂度
• 实际一般观察训练模型复杂度

11. 权重衰退

1. 使用使用均方范数作为硬性限制

$$\begin{gathered} \min \ell (\mathbf{w},b)subjectto \\ mathbf{||w||}^2⩽\theta \end{gathered}$$

2. 使用使用均方范数作为柔性限制

损失函数：
$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$
某种方式在损失函数中添加$\Vert \mathbf{w}{\Vert }^2$，通过非负超参数，正则化常数$\lambda$平衡这个新的额外惩罚的损失
$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2,$$
$L_2$正则化回归的小批量随机梯度下降更新如下式：
$$\begin{array}{rl}\mathbf{w}& \leftarrow \left(1-\eta \lambda \right)\mathbf{w}-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\mathbf{x}}^{(i)}\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right).\end{array}$$
我们根据估计值与观测值之间的差异来更新$\mathbf{w}$

较小的$\lambda$值对应较少约束的$\mathbf{w}$， 而较大的$\lambda$值对$\mathbf{w}$的约束更大。

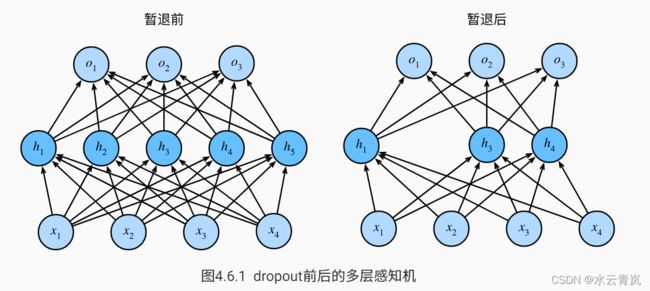
12. 丢弃法dropout

• 丢弃法常用在多重感知机中
• 丢弃法将一些输出项随机置0来控制模型的复杂度
• 丢弃概率是控制模型复杂度的超参数
• 丢弃法在前向传播过程中，计算每一内部层的同时丢弃一些神经元。
• 丢弃法可以避免过拟合，它通常与控制权重向量的维数和大小结合使用的。
• 丢弃法将活性值$\mathbf{h}$替换为具有期望值$\mathbf{h}$的随机变量。
• 丢弃法仅在训练期间使用。

1.加入噪音

在标准丢弃法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。 换言之，每个中间活性值$\mathbf{h}$以暂退概率$p$由随机变量$h^{‘}$替换，如下所示：
KaTeX parse error: No such environment: split at position 8: \begin{̲s̲p̲l̲i̲t̲}̲\begin{aligned}…
其期望值保持不变，即$E[h^{\prime }]=h$

2.使用

$$\begin{array}{r}\mathbf{h}=\sigma ({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1)\\ {\mathbf{h}}^{‘}=\mathbf{d}\mathbf{r}\mathbf{o}\mathbf{p}\mathbf{o}\mathbf{u}\mathbf{t}(\mathbf{h})\\ \mathbf{o}={\mathbf{W}}_2{\mathbf{h}}^{‘}+{\mathbf{b}}_2\\ \mathbf{y}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}(\mathbf{o})\end{array}$$

活性值$\mathbf{h}$替换为具有期望值$\mathbf{h}$的随机变量。

• 丢弃法仅在训练期间使用。

1.加入噪音

在标准丢弃法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。 换言之，每个中间活性值$\mathbf{h}$以暂退概率$p$由随机变量$h^{‘}$替换，如下所示：
$$\begin{array}{r}{h}^{\prime }=\{\begin{array}{ll}0& \text{ 概率为 }p\\ \frac{h}{1-p}& \text{ 其他情况}\end{array}\end{array}$$
其期望值保持不变，即$E[h^{\prime }]=h$

2.使用

$$\begin{array}{r}\mathbf{h}=\sigma ({\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1)\\ {\mathbf{h}}^{‘}=\mathbf{d}\mathbf{r}\mathbf{o}\mathbf{p}\mathbf{o}\mathbf{u}\mathbf{t}(\mathbf{h})\\ \mathbf{o}={\mathbf{W}}_2{\mathbf{h}}^{‘}+{\mathbf{b}}_2\\ \mathbf{y}=\mathbf{s}\mathbf{o}\mathbf{f}\mathbf{t}\mathbf{m}\mathbf{a}\mathbf{x}(\mathbf{o})\end{array}$$