决策树与K-近邻分类随堂笔记（二）

环境：pycharm
语言：python3.6
时间：2019-8-11
遗留问题：

• [ √] cross_val_score()交叉验证的底层算法不了解，尤其是准确率
  在交叉验证时，并没有用到测试集。而是，比如5折验证，每次都是训练集的五分之一去验证，循环5次。参考：https://blog.csdn.net/mangobar/article/details/78501068
• GridSearchCV调参和np.mean(cross_val_score（…））有点晕、
• 随机森林后面还需要看看

引入包

import numpy as np
import os
import pandas as pd
import pydotplus
import matplotlib.pyplot as plt

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, StratifiedKFold   # 分割数据集用的包
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV, cross_val_score  # 模型调参利器,交叉验证
from sklearn.pipeline import Pipeline  # Pipeline可以将许多算法模型串联起来，比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_digits # 手写数字集

from io import StringIO  # 缓存

最近邻方法

最近邻方法也叫K-近邻或K-NN，是一种常见的分类方法。这个方法遵循紧密性假说：当样本之间的距离较好的满足我们设置的方法（或者说条件），我们就足够有理由认为它们属于同一类。
比如：在下面二分类中，我们足够有理由认为：绿球是属于蓝色球类而不是红色球类。这是因为绿球距离蓝球足够的近。

最近邻对测试集的数据进行分类，需要以下3步操作：

• 计算训练集中每个样本之间的距离
• 从训练集中选取K个距离（对测试数据）足够近的样本
  -测试样本的类别被认为和上一步中K个样本的类别相同

在回归问题中应用最近邻方法很简单，仅需将上述步骤做一个小小的改动：第三步不返回分类，而是返回一个数字，即目标变量在邻居中的均值或中位数。

这一方式的显著特点是它具有惰性：当需要对测试样本进行分类时，计算只在预测阶段进行。由于这种特点，最近邻方法事先并不基于训练样本创建模型，这与上文提到的决策树不同。决策树是基于训练集构建的，在预测阶段仅通过遍历决策树就可以实现快速地分类

最近邻的实际应用

• K-NN可以作为一个模型的基线
• 在 Kaggle 竞赛中，k-NN 常常用于构建元特征（即 k-NN 的预测结果作为其他模型的输入），或用于堆叠/混合。
• 最近邻方法还可以扩展到推荐系统等任务中。
• 在大型数据集上，常常使用逼近方法搜索最近邻

k-NN 分类/回归的效果取决于一些参数：

• 邻居数 k。
• 样本之间的距离度量（常见的包括 Hamming，欧几里得，余弦和 Minkowski距离）。注意，大部分距离要求数据在同一尺度下，例如「薪水」特征的数值在千级，「年龄」特征的数值却在百级，如果直接将他们丢进最近邻模型中，「年龄」特征就会受到比较大的影响。
• 邻居的权重（每个邻居可能贡献不同的权重，例如，样本越远，权重越低）。

scikit-learn 的 KNeighborsClassifier 类

sklearn.neighbors.KNeighborsClassifier 类的主要参数为：

• weights：可设为 uniform（所有权重相等），distance（权重和到测试样本的距离成反比），或任何其他用户自定义的函数。
• algorithm（可选）：可设为 brute、ball_tree、KD_tree、auto。若设为brute，通过训练集上的网格搜索来计算每个测试样本的最近邻；若设为 ball_tree 或KD_tree，样本间的距离储存在树中，以加速寻找最近邻；若设为 auto，将基于训练集自动选择合适的寻找最近邻的方法。
• leaf_size（可选）：若寻找最近邻的算法是 BallTree 或 KDTree，则切换为网格搜索所用的阈值。
• metric：可设为 minkowski、manhattan、euclidean、chebyshev 或其他。
  警告:
  根据Nearest Neighbors算法，如果找到两个邻居，例如邻居k+1和k，他们有着一样的距离但是不一样的标签，最后的结果会根据训练数据的顺序来决定。

选择模型参数和交叉验证

机器学习算法的主要任务是可以「泛化」未曾见过的数据。由于我们无法立刻得知模型在新数据上的表现（因为还不知道目标变量的真值），因此有必要牺牲一小部分数据，来验证模型的质量，即将一小部分数据作为留置集。

通常采用下述两种方法之一来验证模型的质量：

留置法。保留一小部分数据（一般是 20% 到 40%）作为留置集，在其余数据上训练模型（原数据集的 60%-80%），然后在留置集上验证模型的质量。
交叉验证。最常见的情形是 k 折交叉验证，如下图所示。

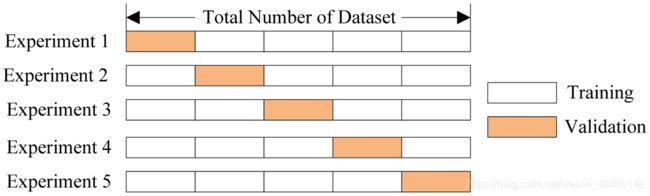
在 k 折交叉验证中，模型在原数据集的 K-1K−1 个子集上进行训练（上图白色部分），然后在剩下的 1 个子集上验证表现，重复训练和验证的过程，每次使用不同的子集（上图橙色部分），总共进行 K 次，由此得到 K 个模型质量评估指数，通常用这些评估指数的求和平均数来衡量分类/回归模型的总体质量。

相比留置法，交叉验证能更好地评估模型在新数据上的表现。然而，当你有大量数据时，交叉验证对机器计算能力的要求会变得很高。

交叉验证是机器学习中非常重要的技术，同时也应用于统计学和经济学领域。它有助于我们进行超参数调优、模型比较、特征评估等其他重要操作。

应用样例：

在客户离网率预测任务中使用决策树和最近邻方法
首先读取数据至 DataFrame 并进行预处理。将 State 特征从 DateFrame 转移到单独的 Series 对象中。我们训练的第一个模型将不包括 State 特征，之后再考察 State 特征是否有用。

import pandas as pd

pd.set_option('display.max_columns', 100)
pd.set_option('display.width', 200)
pd.set_option('display.max_colwidth', 1000)


df = pd.read_csv('./telecom_churn.csv')
# print(df)
df['International plan'] = pd.factorize(df['International plan'])[0]
df['Voice mail plan'] = pd.factorize(df['Voice mail plan'])[0]
# print(df['Voice mail plan'])
df['Churn'] = df['Churn'].astype('int')
states = df['State']
y = df['Churn']
df.drop(['State', 'Churn'], axis=1, inplace=True)

print(df.head())

之后将数据集的 70% 划分为训练集（X_train,y_train），30% 划分为留置集（X_holdout,y_holdout）。留置集的数据在调优模型参数时不会被用到，在调优之后，用它评定所得模型的质量。

接下来，训练 2 个模型：决策树和 k-NN。一开始，我们并不知道如何设置模型参数能使模型表现好，所以可以使用随机参数方法，假定树深（max_dept）为 5，近邻数量（n_neighbors）为 10

X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
                                                          random_state=17)

tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)

tree.fit(X_train, y_train)
knn.fit(X_train, y_train)

tree_pred = tree.predict(X_holdout)
tree_score = accuracy_score(y_holdout, tree_pred)
print('tree accuracy score:', tree_score)
knn_pred = knn.predict(X_holdout)
knn_score = accuracy_score(y_holdout, knn_pred)
print('knn accuracy score:', knn_score)

从上可知，决策树的准确率约为 94%，k-NN 的准确率约为 88.1%，于是仅使用我们假定的随机参数（即没有调参），决策树的表现更好。

现在，使用交叉验证确定树的参数，对每次分割的 max_dept（最大深度 h）和 max_features（最大特征数）进行调优。GridSearchCV() 函数可以非常简单的实现交叉验证，下面程序对每一对 max_depth 和 max_features 的值使用 5 折验证计算模型的表现，接着选择参数的最佳组合。

GridSearchCV() 函数的用法参考这篇文章，总之很强大，可以交叉验证，自动调参。
https://blog.csdn.net/weixin_41988628/article/details/83098130

tree_params = {'max_depth': range(5, 7),
               'max_features': range(16, 18)}

tree_grid = GridSearchCV(tree, tree_params,
                         cv=5, n_jobs=-1, verbose=True)

tree_grid.fit(X_train, y_train)

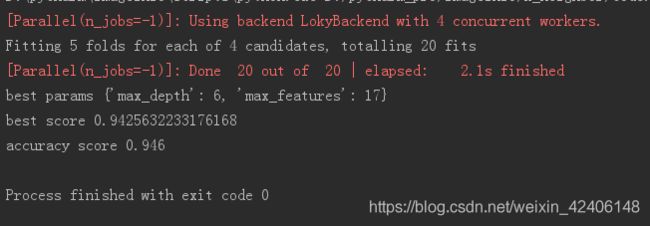
print('best params: ', tree_grid.best_params_)
print('best score: ', tree_grid.best_score_)
print('accuracy score: ', accuracy_score(y_holdout, tree_grid.predict(X_holdout)))

knn_pipe = Pipeline([('scaler', StandardScaler()),
                     ('knn', KNeighborsClassifier(n_jobs=-1))])

knn_params = {'knn__n_neighbors': range(6, 8)}

knn_grid = GridSearchCV(knn_pipe, knn_params,
                        cv=5, n_jobs=-1,
                        verbose=True)

knn_grid.fit(X_train, y_train)

print('best params: ', knn_grid.best_params_, 'best score: ', knn_grid.best_score_)

最终的出来的决策树：

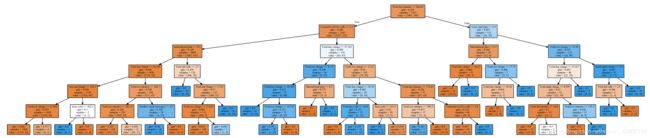
同样，使用交叉验证对K-NN的K值进行调优

Pipeline用法参考：https://blog.csdn.net/qq_32506555/article/details/79912036
*个人理解是让工作过程变成一个队列流程，方便运行中不需要再处理。所谓预处理，感觉也就是提前说明要求而已，并不是真的处理。此处有待研究

从上可知，在 1-9 范围（range 不包括 10）内最优的 k 值为 7，其交叉验证的准确率约为 88.5%，调优后 k-NN 在留置集上的准确率约为 89%。

综上所述，在这个任务里，决策树有着 94%/94.6%（留置法/交叉验证调优后）的准确率，k-NN 有着 88%/89%（留置法/交叉验证调优后）的准确率，显然决策树的表现更好。

使用 RandomForestClassifier() 方法再训练一个随机森林（可以把它想象成一群互相协作的决策树），看看能否在这个任务上有更好的表现。
#########################这里理解的有点不透彻，有待研究###################################

forest = RandomForestClassifier(n_estimators=100, n_jobs=-1,
                                random_state=17)
score_mean = np.mean(cross_val_score(forest, X_train, y_train, cv=5))
print(score_mean)

forest_params = {'max_depth': range(8, 10),
                 'max_features': range(5, 7)}

forest_grid = GridSearchCV(forest, forest_params,
                           cv=5, n_jobs=-1, verbose=True)

forest_grid.fit(X_train, y_train)

print('best params: ',forest_grid.best_params_, 'best score: ', forest_grid.best_score_)
print('accuracy score: ', accuracy_score(y_holdout, forest_grid.predict(X_holdout)))

决策树的复杂情况

为了继续讨论决策树和 k-NN 的优劣，让我们考虑另外一个简单的分类任务，在这个任务中决策树的表现不错但得到的分类边界过于复杂。

首先，在一个平面上创建一组具有 2 个分类的数据点，每个数据点是两个分类中的一个(红色表示x1>x2, 黄色表示x1

# 编造数据
def form_linearly_separable_data(n=500, x1_min=0, x1_max=30,
                                 x2_min=0, x2_max=30):
    data, target = [], []
    for i in range(n):
        x1 = np.random.randint(x1_min, x1_max)
        x2 = np.random.randint(x2_min, x2_max)
        if np.abs(x1 - x2) > 0.5:
            data.append([x1, x2])
            target.append(np.sign(x1 - x2))
    return np.array(data), np.array(target)


X, y = form_linearly_separable_data()

plt.scatter(X[:, 0], X[:, 1], c=y, cmap='autumn', edgecolors='black')
plt.show()

tree = DecisionTreeClassifier(random_state=17).fit(X, y)


def get_grid(data):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    return np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))


xx, yy = get_grid(X)
predicted = tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# print(predicted.shape, tree.predict(np.c_[xx.ravel(), yy.ravel()]).shape, np.c_[xx.ravel(), yy.ravel()].shape, xx.ravel().shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')   # 画分类图
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
            cmap='autumn', edgecolors='black', linewidth=1.5)
plt.title('Easy task. Decision tree compexifies everything')
plt.show

# 可视化成pdf格式
dot_data = StringIO()
export_graphviz(tree, feature_names=['x1', 'x2'],
                out_file=dot_data, filled=True)
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
# Image(value=graph.create_png())
graph.write_pdf("tree_graph1.pdf")

从上可知，决策树构建的边界过于复杂，而且树的深度过深，产生了过拟合现象。

再训练一个 k-NN 模型，看看它在这个任务上的表现情况。

knn = KNeighborsClassifier(n_neighbors=1).fit(X, y)

xx, yy = get_grid(X)
predicted = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
            cmap='autumn', edgecolors='black', linewidth=1.5)
plt.title('Easy task, kNN. Not bad')
plt.show()

从上可知，最近邻方法的表现比决策树好一点，但仍然比不上线性分类器。

在 MNIST 手写数字识别任务中应用决策树和 k-NN

现在可以看看这两个算法应用到实际任务上的表现如何，首先载入 sklearn 内置的 MNIST 手写数字数据集，该数据库中手写数字的图片为 8x8 的矩阵，矩阵中的值表示每个像素的白色亮度。

data = load_digits()
X, y = data.data, data.target

显示一下手写数据，比如;前四个：

f, axes = plt.subplots(1, 4, sharey=True, figsize=(16, 6))
for i in range(4):
    axes[i].imshow(X[i, :].reshape([8, 8]), cmap='Greys')
plt.show()

plt.subplots()的使用参考：https://www.cnblogs.com/komean/p/10670619.html
使用 train_test_split() 方法分割数据集，其中的 70% 作为训练集（X_train，y_train），30% 作为留置集（X_holdout，y_holdout）。使用随机参数训练决策树和 k-NN。

X_train, X_holdout, y_train, y_holdout = train_test_split(
    X, y, test_size=0.3, random_state=17)

tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn_pipe = Pipeline([('scaler', StandardScaler()),
                     ('knn', KNeighborsClassifier(n_neighbors=10))])

tree.fit(X_train, y_train)
knn_pipe.fit(X_train, y_train)

tree_pred = tree.predict(X_holdout)
knn_pred = knn_pipe.predict(X_holdout)
print(accuracy_score(y_holdout, knn_pred), accuracy_score(y_holdout, tree_pred))

从上可知，k-NN 做得更好，不过别忘了我们用的是随机参数。现在，使用交叉验证调优决策树模型，因为这次任务所需考虑的特征比之前任务中的更多，所以可以增加参数的大小。

tree_params = {'max_depth': [10, 20, 30],
               'max_features': [30, 50, 64]}

tree_grid = GridSearchCV(tree, tree_params, cv=5, n_jobs=-1, verbose=True)

tree_grid.fit(X_train, y_train)
print('best params: ',tree_grid.best_params_, 'best score: ', tree_grid.best_score_)
print('accuracy score: ', accuracy_score(y_holdout, tree_grid.predict(X_holdout)))
print(np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5)))

调优后决策树模型的准确率达到了 84.4%，但还不到使用随机参数的 k-NN 的准确率（97%）。使用交叉验证调优 k-NN 模型后准确率可以达到98.65%。

print(np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5)))

从这个任务中得到的结论（同时也是一个通用的建议）：首先查看简单模型（决策树、最近邻）在你的数据上的表现，因为可能仅使用简单模型就已经表现得足够好了。

最近邻方法的复杂情形

下面考虑另一种情况，即在一个分类问题中，某个特征直接和目标变量成比例的情况。

def form_noisy_data(n_obj=1000, n_feat=100, random_seed=17):
    np.seed = random_seed
    y = np.random.choice([-1, 1], size=n_obj)
    # 第一个特征与目标成比例
    x1 = 0.3 * y
    # 其他特征为噪声
    x_other = np.random.random(size=[n_obj, n_feat - 1])
    return np.hstack([x1.reshape([n_obj, 1]), x_other]), y


X, y = form_noisy_data()
print(X.shape, y.shape)

np.hstack()用法参考：https://blog.csdn.net/m0_37393514/article/details/79538748

使用最近邻方法训练模型后，查看交叉验证和留置集的准确率，并绘制这两个准确率随 n_neighbors 最近邻数目 参数变化的曲线，这样的曲线被称为验证曲线。

X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3, random_state=17)


cv_scores, holdout_scores = [], []
n_neighb = [1, 2, 3, 5] + list(range(50, 550, 50))
# print(n_neighb)

for k in n_neighb:

    knn_pipe = Pipeline([('scaler', StandardScaler()),
                         ('knn', KNeighborsClassifier(n_neighbors=k))])
    cv_scores.append(np.mean(cross_val_score( knn_pipe, X_train, y_train, cv=5)))  # 这里注意第一个参数，是交叉验证
    knn_pipe.fit(X_train, y_train)
    holdout_scores.append(accuracy_score(y_holdout, knn_pipe.predict(X_holdout)))

plt.plot(n_neighb, cv_scores, label='CV')
plt.plot(n_neighb, holdout_scores, label='holdout')
plt.title('Easy task. kNN fails')
plt.legend()
plt.show()

上图表明，即使我们尝试在较广范围内改变 n_neighbors 参数，基于欧几里得距离的 k-NN 在这个问题上依旧表现不佳。

下面用决策树训练一个模型，看看它在这个任务上的表现如何。

tree = DecisionTreeClassifier(random_state=17, max_depth=1)
tree_cv_score = np.mean(cross_val_score(tree, X_train, y_train, cv=5))
tree.fit(X_train, y_train)
tree_holdout_score = accuracy_score(y_holdout, tree.predict(X_holdout))
print('Decision tree. CV: {}, holdout: {}'.format(
    tree_cv_score, tree_holdout_score))

在这一任务中，决策树完美地解决了问题，在交叉验证和留置集上都得到了 100% 的准确率。其实，k-NN 之所以在这个任务上表现不佳并非该方法本身的问题，而是因为使用了欧几里得距离，因为欧几里得距离没能察觉出有一个特征（成比例）比其他所有特征（噪声）更重要。

决策树和最近邻方法的优势和劣势

决策树
优势：

• 生成容易理解的分类规则，这一属性称为模型的可解释性。例如它生成的规则可能是「如果年龄不满 25岁，并对摩托车感兴趣，那么就拒绝发放贷款」。
• 很容易可视化，即模型本身（树）和特定测试对象的预测（穿过树的路径）可以「被解释」训练和预测的速度快。
• 较少的参数数目。
• 支持数值和类别特征。
  劣势：
• 决策树对输入数据中的噪声非常敏感，这削弱了模型的可解释性。
• 决策树构建的边界有其局限性：它由垂直于其中一个坐标轴的超平面组成，在实践中比其他方法的效果要差。
• 我们需要通过剪枝、设定叶节点的最小样本数、设定树的最大深度等方法避免过拟合。
• 不稳定性，数据的细微变动都会显著改变决策树。这一问题可通过决策树集成方法来处理（以后的实验会介绍）。
• 搜索最佳决策树是一个「NP 完全」（NP-Complete）问题。了解什么是 NP-Complete 请点击 这里。实践中使用的一些推断方法，比如基于最大信息增益进行贪婪搜索，并不能保证找到全局最优决策树。
• 倘若数据中出现缺失值，将难以创建决策树模型。Friedman 的 CART 算法中大约 50% 的代码是为了处理数据中的缺失值（现在 sklearn 实现了这一算法的改进版本）。
• 这一模型只能内插，不能外推（随机森林和树提升方法也是如此）。也就是说，倘若你预测的对象在训练集所设置的特征空间之外，那么决策树就只能做出常数预测。比如，在我们的黄球和蓝球的例子中，这意味着模型将对所有位于 >19 或 <0 的球做出同样的预测。

最近邻方法
优势：

• 实现简单。
• 研究很充分。
• 通常而言，在分类、回归、推荐问题中第一个值得尝试的方法就是最近邻方法。
• 通过选择恰当的衡量标准或核，它可以适应某一特定问题。

劣势：

• 和其他复合算法相比，这一方法速度较快。但是，现实生活中，用于分类的邻居数目通常较大（100-150），在这一情形下，k-NN不如决策树快。
• 如果数据集有很多变量，很难找到合适的权重，也很难判定哪些特征对分类/回归不重要。
• 依赖于对象之间的距离度量，默认选项欧几里得距离常常是不合理的。你可以通过网格搜索参数得到良好的解，但在大型数据集上的耗时很长。
• 没有理论来指导我们如何选择邻居数，故而只能进行网格搜索（尽管基本上所有的模型，在对其超参数进行调整时都使用网格搜索的方法）。在邻居数较小的情形下，该方法对离散值很敏感，也就是说，有过拟合的倾向。
• 由于「维度的诅咒」，当数据集存在很多特征时它的表现不佳。

大杂烩代码笔记过程

import numpy as np
import os
import pandas as pd
import pydotplus
import matplotlib.pyplot as plt

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, StratifiedKFold   # 分割数据集用的包
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV, cross_val_score  # 模型调参利器,交叉验证
from sklearn.pipeline import Pipeline  # Pipeline可以将许多算法模型串联起来，比如将特征提取、归一化、分类组织在一起形成一个典型的机器学习问题工作流。
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_digits # 手写数字集


from io import StringIO  # 缓存


# 数据显示问题
pd.set_option('display.max_columns', 100)
pd.set_option('display.width', 200)
pd.set_option('display.max_colwidth', 1000)


df = pd.read_csv('./telecom_churn.csv')
# print(df)
df['International plan'] = pd.factorize(df['International plan'])[0]
df['Voice mail plan'] = pd.factorize(df['Voice mail plan'])[0]
# print(df['Voice mail plan'])
df['Churn'] = df['Churn'].astype('int')
states = df['State']
y = df['Churn']
df.drop(['State', 'Churn'], axis=1, inplace=True)

# print(df.head())
X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
                                                          random_state=17)

tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)


tree.fit(X_train, y_train)
knn.fit(X_train, y_train)

tree_pred = tree.predict(X_holdout)
tree_score = accuracy_score(y_holdout, tree_pred)
# print('tree accuracy score:', tree_score)
knn_pred = knn.predict(X_holdout)
knn_score = accuracy_score(y_holdout, knn_pred)
# print('knn accuracy score:', knn_score)
###########################################################################################

# tree_params = {'max_depth': range(5, 7),
#                'max_features': range(16, 18)}
#
# tree_grid = GridSearchCV(tree, tree_params,
#                          cv=5, n_jobs=-1, verbose=True)
#
# tree_grid.fit(X_train, y_train)
#
# # print('best params: ', tree_grid.best_params_)
# # print('best score: ', tree_grid.best_score_)
# # print('accuracy score: ', accuracy_score(y_holdout, tree_grid.predict(X_holdout)))
#
# dot_data = StringIO()
# os.environ["PATH"] += os.pathsep + 'D:/Graphviz/bin/'
# export_graphviz(tree_grid.best_estimator_, feature_names=df.columns,
#                 out_file=dot_data, filled=True)
# graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
# Image(value=graph.create_png())
# graph.write_pdf("tree_graph.pdf")
#################################################################################

#
# knn_pipe = Pipeline([('scaler', StandardScaler()),
#                      ('knn', KNeighborsClassifier(n_jobs=-1))])
#
# knn_params = {'knn__n_neighbors': range(6, 8)}
#
# knn_grid = GridSearchCV(knn_pipe, knn_params,
#                         cv=5, n_jobs=-1,
#                         verbose=True)
#
# knn_grid.fit(X_train, y_train)
#
# # print('best params: ', knn_grid.best_params_, 'best score: ', knn_grid.best_score_)
# # print('accuracy score: ', accuracy_score(y_holdout, knn_grid.predict(X_holdout)))
#
# forest = RandomForestClassifier(n_estimators=100, n_jobs=-1,
#                                 random_state=17)
# score_mean = np.mean(cross_val_score(forest, X_train, y_train, cv=5))
# # print(score_mean)
#
# forest_params = {'max_depth': range(8, 10),
#                  'max_features': range(5, 7)}
#
# forest_grid = GridSearchCV(forest, forest_params,
#                            cv=5, n_jobs=-1, verbose=True)
#
# forest_grid.fit(X_train, y_train)

# print('best params: ',forest_grid.best_params_, 'best score: ', forest_grid.best_score_)
# print('accuracy score: ', accuracy_score(y_holdout, forest_grid.predict(X_holdout)))


###################################################################################################

# 编造数据
# def form_linearly_separable_data(n=500, x1_min=0, x1_max=30,
#                                  x2_min=0, x2_max=30):
#     data, target = [], []
#     for i in range(n):
#         x1 = np.random.randint(x1_min, x1_max)
#         x2 = np.random.randint(x2_min, x2_max)
#         if np.abs(x1 - x2) > 0.5:
#             data.append([x1, x2])
#             target.append(np.sign(x1 - x2))
#     return np.array(data), np.array(target)

#
# X, y = form_linearly_separable_data()
# plt.scatter(X[:, 0], X[:, 1], c=y, cmap='autumn', edgecolors='black')
# # plt.show()
#
# tree = DecisionTreeClassifier(random_state=17).fit(X, y)


# def get_grid(data):
#     x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
#     y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
#     return np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

#
# xx, yy = get_grid(X)
# predicted = tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# # print(predicted.shape, tree.predict(np.c_[xx.ravel(), yy.ravel()]).shape, np.c_[xx.ravel(), yy.ravel()].shape, xx.ravel().shape)
# plt.pcolormesh(xx, yy, predicted, cmap='autumn')   # 画分类图
# plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
#             cmap='autumn', edgecolors='black', linewidth=1.5)
# plt.title('Easy task. Decision tree compexifies everything')
# # plt.show()
#
# # 可视化成pdf格式
# dot_data = StringIO()
# export_graphviz(tree, feature_names=['x1', 'x2'],
#                 out_file=dot_data, filled=True)
# graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
# # Image(value=graph.create_png())
# graph.write_pdf("tree_graph1.pdf")


############################# 看看K-NN的效果怎么样 #########################################################


# knn = KNeighborsClassifier(n_neighbors=1).fit(X, y)
#
# xx, yy = get_grid(X)
# predicted = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# plt.pcolormesh(xx, yy, predicted, cmap='autumn')
# plt.scatter(X[:, 0], X[:, 1], c=y, s=100,
#             cmap='autumn', edgecolors='black', linewidth=1.5)
# plt.title('Easy task, kNN. Not bad')
# plt.show()

######################在 MNIST 手写数字识别任务中应用决策树和 k-NN ############################



# data = load_digits()
# X, y = data.data, data.target
# # print(X.shape)
# # X[0, :].reshape([8, 8])
# # print(X[0, :])
#
# f, axes = plt.subplots(1, 4, sharey=True, figsize=(16, 6))
# for i in range(4):
#     axes[i].imshow(X[i, :].reshape([8, 8]), cmap='Greys')
# # plt.show()
#
#
# X_train, X_holdout, y_train, y_holdout = train_test_split(
#     X, y, test_size=0.3, random_state=17)
#
# tree = DecisionTreeClassifier(max_depth=5, random_state=17)
# knn_pipe = Pipeline([('scaler', StandardScaler()),
#                      ('knn', KNeighborsClassifier(n_neighbors=10))])
#
#
#
# tree.fit(X_train, y_train)
# knn_pipe.fit(X_train, y_train)
#
# tree_pred = tree.predict(X_holdout)
# knn_pred = knn_pipe.predict(X_holdout)
# print(accuracy_score(y_holdout, knn_pred), accuracy_score(y_holdout, tree_pred))
#
# tree_params = {'max_depth': [10, 20, 30],
#                'max_features': [30, 50, 64]}
#
# tree_grid = GridSearchCV(tree, tree_params, cv=5, n_jobs=-1, verbose=True)
#
# tree_grid.fit(X_train, y_train)
# print('best params: ',tree_grid.best_params_, 'best score: ', tree_grid.best_score_)
# print('accuracy score: ', accuracy_score(y_holdout, tree_grid.predict(X_holdout)))
#
# print(np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5)))

#############################最近邻方法的复杂情形#######################################################


def form_noisy_data(n_obj=1000, n_feat=100, random_seed=17):
    np.seed = random_seed
    y = np.random.choice([-1, 1], size=n_obj)
    # 第一个特征与目标成比例
    x1 = 0.3 * y
    # 其他特征为噪声
    # print(x1.shape, x1.reshape([n_obj, 1]).shape)
    x_other = np.random.random(size=[n_obj, n_feat - 1])
    # print(x_other.shape)
    return np.hstack([x1.reshape([n_obj, 1]), x_other]), y


X, y = form_noisy_data()
# print(X.shape, y.shape)

X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3, random_state=17)


cv_scores, holdout_scores = [], []
# cv_scores1 = []
n_neighb = [1, 2, 3, 5] + list(range(50, 550, 50))
# print(n_neighb)

for k in n_neighb:

    knn_pipe = Pipeline([('scaler', StandardScaler()),
                         ('knn', KNeighborsClassifier(n_neighbors=k))])
    cv_scores.append(np.mean(cross_val_score( knn_pipe, X_train, y_train, cv=5)))  # 这里注意第一个参数，是交叉验证
    # cv_scores1.append(np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=k), X_train, y_train, cv=5)))
    knn_pipe.fit(X_train, y_train)
    holdout_scores.append(accuracy_score(y_holdout, knn_pipe.predict(X_holdout)))

plt.plot(n_neighb, cv_scores, label='CV')
# plt.plot(n_neighb, cv_scores1, label='CV1111')
plt.plot(n_neighb, holdout_scores, label='holdout')
plt.title('Easy task. kNN fails')
plt.legend()
plt.show()




tree = DecisionTreeClassifier(random_state=17, max_depth=1)
tree_cv_score = np.mean(cross_val_score(tree, X_train, y_train, cv=5))
tree.fit(X_train, y_train)
tree_holdout_score = accuracy_score(y_holdout, tree.predict(X_holdout))
print('Decision tree. CV: {}, holdout: {}'.format(
    tree_cv_score, tree_holdout_score))