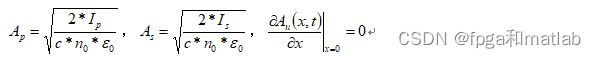非线性光学散射偏微分方程组的matlab求解仿真

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

边值条件：

 条件：

       Ap、As、Au都表示瞬时幅度，c=3*10^8，ε0=8.85*10^-12，ρ0=2500，n0=1.0003，n=1.46， va=5980，αa=0.2/4.343*10^-3，γ=(n*n-1)*(n*n+2)/3，ks=kp=5.92*10^6，ka=ku=1.18*10^7，Ip=2*10^15，Is=100，L是x的空间长度人为设定为1厘米，时间长度t人为设定为1毫秒。方程里i是虚数单位，方程里*是共轭，x表示空间一维，t表示时间维，第三个方程里Aa应该是Au。有需要再补充

要求：

       程序里需要n、L、t、αa 、Ip 、Is 、ks、kp、ka等基本常数都可以灵活微调（就是说作为全局变量的意思吧）；用常用算法比如有限差分法解方程组。

     P，S，U三个光P和U是同方向传播的，S为反方向传播，那么差分方程如下所示：

 ★化简得到如下的式子：

 ★进一步简化得到：

     显然，上面的公式是一组隐性的差分方程组，因此，我们需要做近似，然后再做迭代进行处理，近似做法如下所示。 

根据上面最后一个公式进行编程。

二、核心程序

.............................................................
%%
%利用有限差分法将偏微分方程转换为差分方程形式
K11 =  1 + (dx*n)/(dt*c);
K12 = -1;
K13 = (dx*n)/(dt*c);
K14 = (dx*r*ku*kp)/(2*n*n);
K15 = -1*i*(r*c*kp)/(2*n*n);

K21 = -1 + (dx*n)/(dt*c);
K22 =  1;
K23 = (dx*n)/(dt*c);
K24 = (dx*r*ku*ks)/(2*n*n);
K25 = -1*i*(r*c*kp)/(2*n*n);

K31 = -1 + (aa*dx)/2 + dx*(1+i*aa/ku)/(va*dt);
K32 =  1;
K33 =  dx*(1+i*aa/ku)/(va*dt);
K34 = -1*(dx*e0*r)/(4*p0*va*va);
 

%%Ap(Lx,Tx+1)   = (-K12*Ap(Lx-1,Tx+1) + K13*Ap(Lx,Tx) + K14*As(Lx,Tx+1)*As(Lx,Tx+1) + K15*As(Lx,Tx+1)*(Au(Lx,Tx+1)-Au(Lx-1,Tx+1)))/K11;
%Ap(Lx,Tx+1)    = (-K12*Ap(Lx-2,Tx)   + K13*Ap(Lx,Tx) + K14*As(Lx-1,Tx)*As(Lx-1,Tx) + K15*As(Lx-1,Tx)*(Au(Lx-1,Tx)-Au(Lx-2,Tx)))/K11;

%Lx2            = L-Lx;
%%As(L-Lx,Tx+1) = (-K22*As(L-Lx+1,Tx+1) + K23*As(L-Lx,Tx) + K24*conj(Au(L-Lx,Tx+1))*Ap(L-Lx,Tx+1) + K25*Ap(L-Lx,Tx+1)*(conj(Au(L-Lx,Tx+1))-conj(Au(L-Lx-1,Tx+1))))/K21;
%As(Lx2,Tx+1)   = (-K22*As(Lx2+2,Tx)    + K23*As(Lx2,Tx)  + K24*conj(Au(Lx2+1,Tx)) *Ap(Lx2+1,Tx)    + K25*Ap(Lx2+1,Tx)*(conj(Au(Lx2+1,Tx))-conj(Au(Lx2,Tx))))/K21;


%%Au(Lx,Tx+1)   = (-K32*Au(Lx-1,Tx+1) + K33*Au(Lx,Tx) + K34*conj(As(Lx,Tx+1))*Ap(Lx,Tx+1))/K31;
%Au(Lx,Tx+1)   = (-K32*Au(Lx-2,Tx)    + K33*Au(Lx,Tx) + K34*conj(As(Lx-1,Tx))*Ap(Lx-1,Tx))/K31;

Ap(1,1) = sqrt(2*Ip/c/n0/e0);
As(L,1) = sqrt(2*Is/c/n0/e0);
Au(1,1) = 0;  

%下面使用差分迭代的方法来对三个变量进行求解
for Lx = 3:L-3%距离微分 
    ttt = 0;
    for Tx = 1:T-1%时间微分
        fprintf('距离微分:');
        fprintf('%2.4f  |  ',Lx);
        fprintf('时间微分:');
        fprintf('%2.4f',Tx);
        fprintf('\n');
        Lx2            =  L-Lx;
        
        Ap(Lx,Tx+1)    = (-K12*Ap(Lx-2,Tx)     + K13*Ap(Lx,Tx)   + K14*As(Lx+1,Tx)*As(Lx+1,Tx)           + K15*As(Lx-1,Tx)*(Au(Lx-1,Tx)-Au(Lx-2,Tx)))/K11;
        
        As(Lx2,Tx+1)   = (-K22*As(Lx2+2,Tx)    + K23*As(Lx2,Tx)  + K24*conj(Au(Lx2+1,Tx)) *Ap(Lx2+1,Tx)  + K25*Ap(Lx2+1,Tx)*(conj(Au(Lx2+1,Tx))-conj(Au(Lx2,Tx))))/K21;
        
        Au(Lx,Tx+1)    = (-K32*Au(Lx-2,Tx)     + K33*Au(Lx,Tx)   + K34*conj(As(Lx-1,Tx))*Ap(Lx-1,Tx))/K31;    
    end 
    Ap(Lx ,:) = Ap(Lx ,:)/1e2;
    As(Lx2,:) = As(Lx2,:);
    Au(Lx ,:) = Au(Lx ,:)/1e2;
end
.........................................................................

三、测试结果

    这里，通过以动态效果进行仿真，从而直接给出同时反映波空间和时间的二维动态效果图。当波接触的时候，会产生相互的影响。具体见仿真结果。

  

 A16-18