数字图像处理合集——图像分割

实现：
1、掌握大津阈值分割算法,理解大津阈值分割数学原理是使得分割后各个像素类的类间方差最大，并能编写程序实现。
2、掌握微分算子边缘检测算法,理解一阶和二阶微分算子的数学原理和在图像中代表的物理意义，并能够程序实现。
3、掌握霍夫变换算法,理解霍夫直线检测数学原理的推导过程及其图像处理的效果，并能够程序实现。

1、大津阈值分割算法关键代码及注释。
使用函数计算最佳阈值，在主函数内带入到接口函数显示图像。在自定义函数内通过计算类间方差获得最佳阈值，在0~255内进行循环计算。自定义函数如下所示。

int thresholdOtsu(Mat & image)
{
	//【1】
	int thresh;
	int pixNumber = image.cols * image.rows;        //图像总像素点
	int pixCount[256] = { 0 };                      //每个灰度值所占像素个数
	//【2】统计每个灰度级中像素的个数  
	for (int i = 0; i < image.rows; i++)
	{
		for (int j = 0; j < image.cols; j++)
		{
			pixCount[image.at<uchar>(i, j)]++;
		}
	}
	//【3】遍历所有从0到255灰度级的阈值分割条件，测试哪一个的类间方差最大
	float PixBackground = 0;
	float GrayBackground = 0;
	float GrayAverageBackground = 0;
	float PixForeground = 0;
	float GrayForeground = 0;
	float GrayAverageForeground = 0;
	float InterclassVariance = 0;
	float InterclassVarianceMax = 0;
	//[1]外层循环选定阈值,并计算当前阈值对应的类间方差
	for (int i = 0; i < 256; i++)
	{
		PixBackground = PixForeground = GrayBackground = GrayForeground = GrayAverageBackground = GrayAverageForeground = InterclassVariance = 0;
		//[2]内层循环区分前景和背景
		for (int j = 0; j < 256; j++)
		{
			if (j <= i)         //背景
			{
				PixBackground += pixCount[j];
				GrayBackground += j * pixCount[j];
			}
			else                //前景
			{
				PixForeground += pixCount[j];
				GrayForeground += j * pixCount[j];
			}
		}
		GrayAverageBackground = GrayBackground / PixBackground;
		GrayAverageForeground = GrayForeground / PixForeground;
		//当前类间方差计算
		InterclassVariance = (float)(PixBackground *PixForeground* pow((GrayAverageBackground - GrayAverageForeground), 2));

		if (InterclassVariance > InterclassVarianceMax)
		{
			InterclassVarianceMax = InterclassVariance;
			thresh = i;
		}
	}
	return thresh;
}

实现效果：
使用大津阈值分割算法获得的目标背景分割结果如图1所示。

2、一阶/二阶微分算子检测水平边缘、垂直边缘关键代码及注释。
使用sobel算子进行一阶水平、垂直边缘检测。sobel算子实现代码如下所示：

int sobel(Mat &srcImage)
{
	Mat gray_x, gray_y;
	Mat abs_gray_x, abs_gray_y, dst;
	if (!srcImage.data)
		return -1;
	Sobel(srcImage, gray_x, CV_16S, 1, 0, 3, 1, 1, BORDER_DEFAULT);
	convertScaleAbs(gray_x, abs_gray_x);
	imshow("x方向", abs_gray_x);
	Sobel(srcImage, gray_y, CV_16S, 0, 1, 3, 1, 1, BORDER_DEFAULT);
	convertScaleAbs(gray_y, abs_gray_y);
	imshow("y方向", abs_gray_y);
	addWeighted(abs_gray_x, 0.5, abs_gray_y, 0.5, 0, dst);
	imshow("效果图", dst);
	waitKey(0);
	return 0;
}
使用Laplacian算子完成二阶水平、垂直边缘检测，实现代码如下所示：
int Laplacian(Mat & src)
{
	if (src.empty())
	{
		cout << "Can't load the image" << endl;
		return -1;
	}
	imshow("src", src);
	//边缘检测的算法主要是基于图像强度的一阶和二阶导数，但导数通常对噪声很敏感，
	//因此必须采用滤波器来改善与噪声有关的边缘检测器的性能
	Mat blursrc;
	GaussianBlur(src, blursrc, Size(3, 3), 0, 0);
	//Laplace变换
	Mat dst;
	Laplacian(src, dst, CV_16S, 3);
	convertScaleAbs(dst, dst);
	imshow("检测结果", dst);
	waitKey(0);
	return 0;
}

实现效果：
使用的测试原图如图2所示。最终使用sobel算子进行边缘检测的实验结果如图3、图4、图5所示。使用Laplacian算子进行二阶边缘检测的实验结果如图6所示，使用同样的检测图。
检测原图：

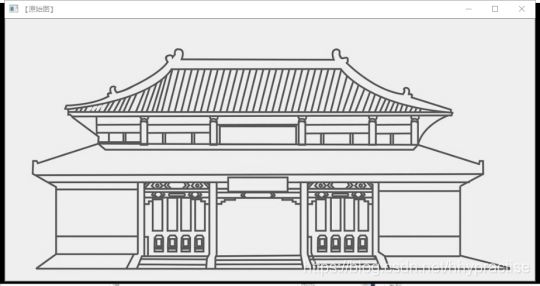
x方向的sobel算子检测结果：

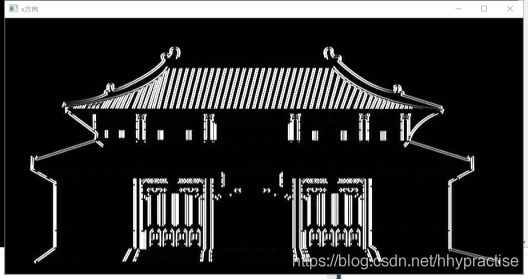
y方向的sobel算子检测结果：

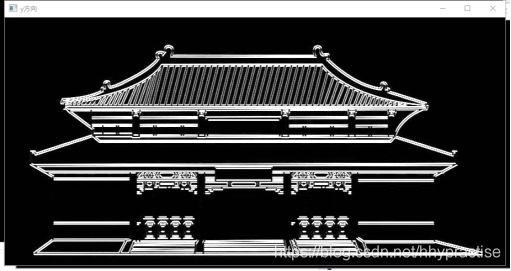
使用sobel算子检测的实验结果：

使用Laplacian算子的检测结果：

3、霍夫变换直线检测算法关键代码及注释。
自定义霍夫检测函数，先用Canny进行一次边缘检测，使用HoughLines进行霍夫线变换，然后使用for循环依次在图中绘制出每条线段。霍夫变换实现关键代码如下所示：

int Hough_Transform(Mat & srcImage)
{
	Mat midImage;//临时变量和目标图的定义  
	//【2】进行边缘检测  
	Canny(srcImage, midImage, 50, 200, 3);//进行一此canny边缘检测  
	//【3】进行霍夫线变换  
	vector<Vec2f> lines;//定义一个矢量结构lines用于存放得到的线段矢量集合  
	HoughLines(midImage, lines, 1, CV_PI / 180, 150, 0, 0);
	//【4】依次在图中绘制出每条线段  
	for (size_t i = 0; i < lines.size(); i++)
	{
		float rho = lines[i][0], theta = lines[i][1];
		Point pt1, pt2;
		double a = cos(theta), b = sin(theta);
		double x0 = a * rho, y0 = b * rho;
		pt1.x = cvRound(x0 + 1000 * (-b));
		pt1.y = cvRound(y0 + 1000 * (a));
		pt2.x = cvRound(x0 - 1000 * (-b));
		pt2.y = cvRound(y0 - 1000 * (a));
	}
	//【5】显示原始图    
	imshow("【原始图】", srcImage);
	//【6】边缘检测后的图   
	imshow("【边缘检测后的图】", midImage);
	waitKey(0);
	return 0;
}

实现结果：
霍夫变换检测直线使用图2作为检测图，实验结果如图7所示。

合集入口

测试资源下载入口