Lecture 4 Sequence as input
Lecture 4: Sequence as input
文章目录
- Self-attention
-
- Sophisticated Input
-
- Vector set as input
-
- 文字处理
- 音频处理
- Graph as input
- What is the output?
-
- Each vector has a label
-
- Example
- The whole sequence has a label
-
- Example
- Model decides the number of labels itself (**Seq2Seq**)
- Sequence Labeling
- Self-attention
-
- Input and output
- Self-attention in the view of matrix multiplication
-
- Step 1: 计算 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi
- Step 2: 计算 α \alpha α
- Step 3: 计算 b i {\bf b}^i bi
- Brief Summary
- Multi-head Self-attention
- Positional Encoding
- Applications of self-attention
-
- NLP
- Speech
- Image
- Self-attention v.s. CNN
Self-attention
Sophisticated Input
Input is a vector:

Input is a set of vectors:

Vector set as input
文字处理
假设网络的输入是一个句子,我们需要将句子中的每一个词都用一个向量来表示。那么,我们的模型输入将会是一个 Vector Set,并且每一次输入的 Vector Set 的大小会不同。将用向量来表示词汇的方法如下所示:
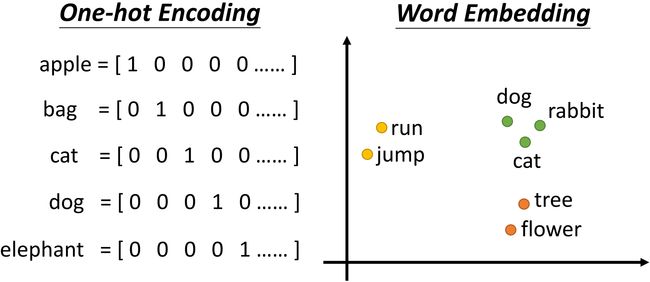
One-hot Encoding 建立一个很长的向量,每一个维度对应一个词汇。缺点也很明显,这种方法忽略掉了词语之间的关系(词语间语义的关系);比如说,很难从 One-hot Encoding 中看出 cat 和 dog 都是动物这层关系。
Word Embedding 也使用向量来表示词语,但这些向量包含了语义的关系。如上图所示,可以看到“动词”、“动物”、“植物”类的词汇往往都分别聚集成一块。
音频处理

一个窗口(Window)内的音频信号可以描述成一个向量,这个向量也叫做帧(Frame),长度通常是 25 m s 25ms 25ms;为了描述整段的音频信号,窗口会进行滑动,向后滑动 10 m s 10ms 10ms;那么 1 s 1s 1s 内就有 100 100 100 个向量。
Graph as input


What is the output?
Each vector has a label

输入和输出的长度保持一致,输入 n n n 个 vector 就输出 n n n 个 scalar 或 class。
Example

常见的应用:词性标注;语音辨识;社交网络中每个结点的特性。
The whole sequence has a label

无论输入有多长,都只会有一个输出。
Example
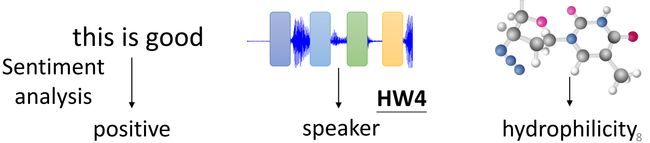
常见应用:情感分析;识别演讲人;有机物的亲水性如何。
Model decides the number of labels itself (Seq2Seq)

我们并不知道将会有多少输出,需要模型自己决定。
Sequence Labeling
本节主要关注 Each vector has a label 这一情况,又叫做 Sequence Labeling。

如果我们考虑用全连接网络来解决词性标注的问题,那将会有一个明显的问题 —— 我们期待 s a w \color{blue} saw saw 通过 FC 后输出的是动词, s a w \color{orange}saw saw 通过 FC 后输出的是名词,而对于 FC 来说,输入的 s a w \color{black}saw saw 没有任何区别,因此它们会得到同样的输出。
为了解决上述问题,我们尝试让 FC 考虑上下文的信息,我们将前后几个相邻向量(一个 window)都输入 FC 中。那如果问题需要考虑一整个 Sequence 该怎么办呢?—— 引入 Self - attention
Self-attention

Self-attention 的处理流程如上图所示,将 Sequence 中的所有 Vector 输入 Self-attention,输入 n n n 个 Vector 就输出 n n n 个 Vector,且这 n n n 个 Vector 都考虑了整个 Sequence 的信息。将这些 Vector 再输入到 FC 中,最终再输出 scalar 或者 class。
Input and output

Self-attention 的输入可以来自原始的 input vector 或者是 hidden layer 的输出。每一个输出向量 b \bf b b 都考虑了输入向量 a \bf a a。接下来将详细解释输出向量 b 1 {\bf b}^1 b1 的产生过程。
计算 α \alpha α:

首先,根据 a 1 a^1 a1 找出这个 sequence 中所有与 a 1 a^1 a1 相关的向量,sequence 中其余向量与 a 1 a^1 a1 的关联程度用 α \alpha α 表示。那么, α \alpha α 如何计算呢?引入计算 attention 的模组。
Dot-product
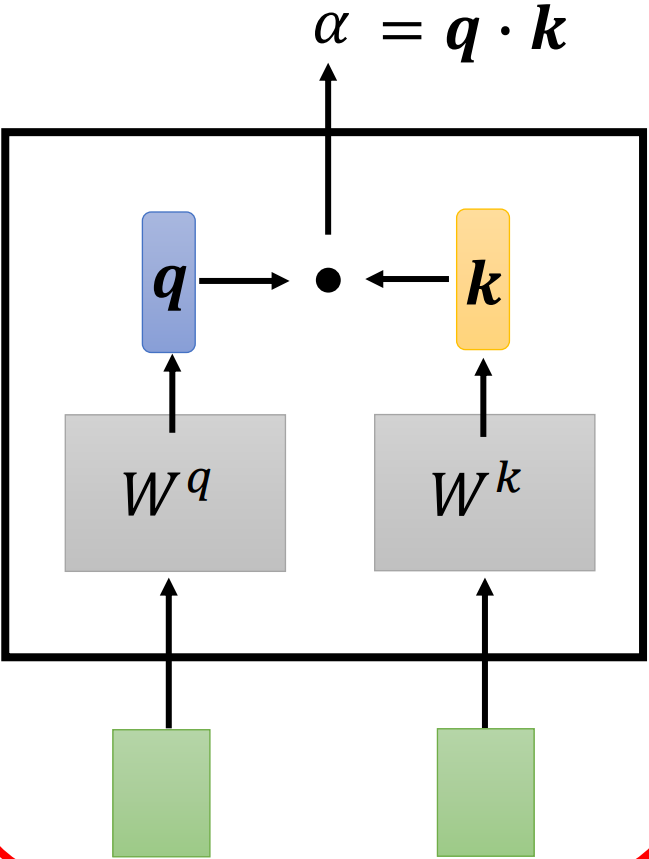
两个输入向量分别乘上矩阵 W q W^q Wq 和 W k W^k Wk 得到向量 q \bf q q 和 k \bf k k, α = q ⋅ k \alpha=\bf q \cdot \bf k α=q⋅k。Transformer 中使用的是这种方法。
Additive
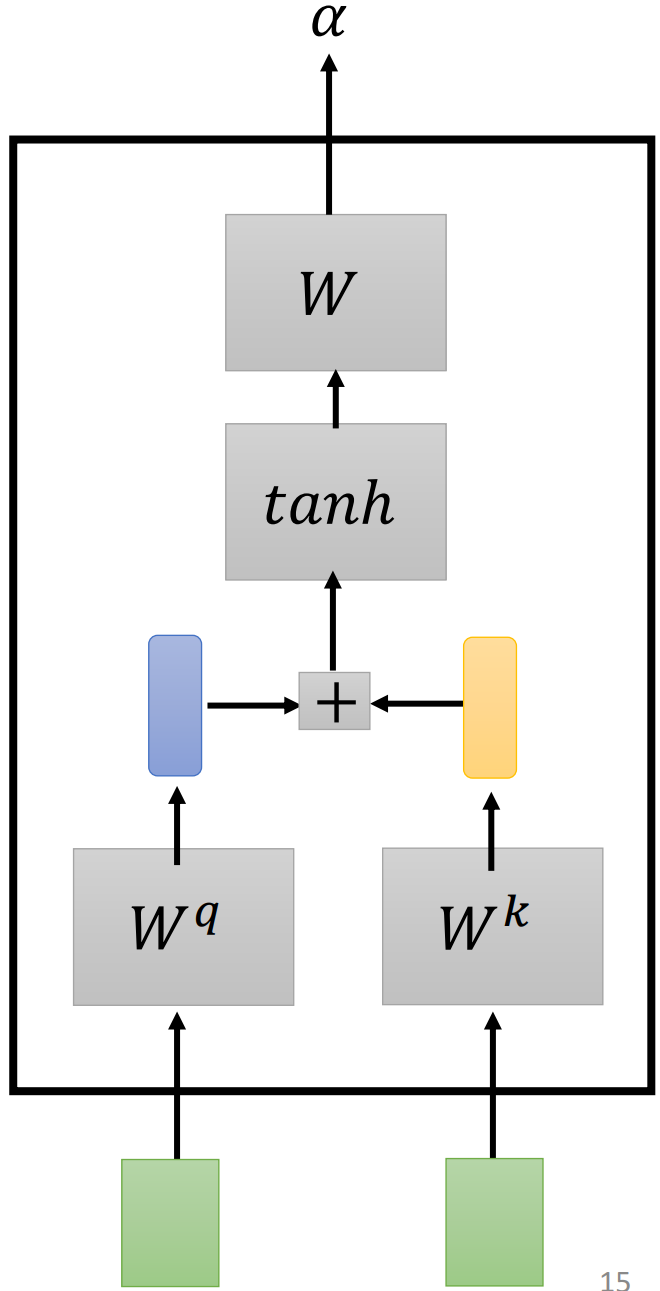
两个输入向量分别乘上矩阵 W q W^q Wq 和 W k W^k Wk 得到向量 q \bf q q 和 k \bf k k,将这两个向量连接起来输入到激活函数中,再经过一个 Transform 得到 α \alpha α。

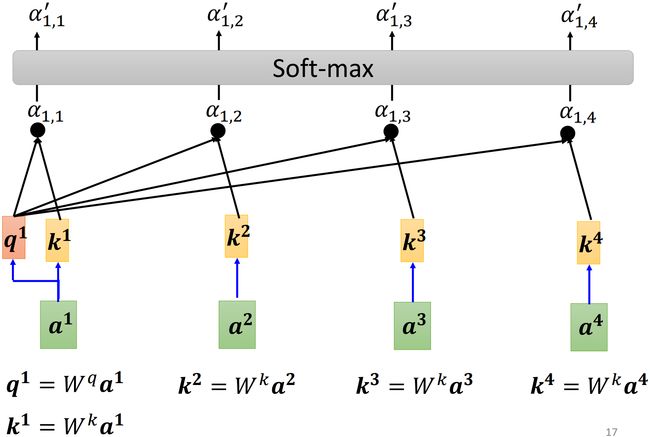
如上图所示, a 1 {\bf a}^1 a1 乘上 W q {\rm W}^q Wq 作为 query q 1 {\bf q}^1 q1, a 1 , a 2 , a 3 {\bf a}^1,\ {\bf a}^2,\ {\bf a}^3 a1, a2, a3 都乘上 W k {\rm W}^k Wk 作为 key k 2 , k 3 , k 4 {\bf k}^2,\ {\bf k}^3,\ {\bf k}^4 k2, k3, k4。 q 1 {\bf q}^1 q1 分别和 k 2 , k 3 , k 4 {\bf k}^2,\ {\bf k}^3,\ {\bf k}^4 k2, k3, k4 做点积得到 α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,2},\ \alpha_{1,3},\ \alpha_{1,4} α1,2, α1,3, α1,4,这些 α \alpha α 也叫做 attention score。
计算 b 1 {\bf b}^1 b1:
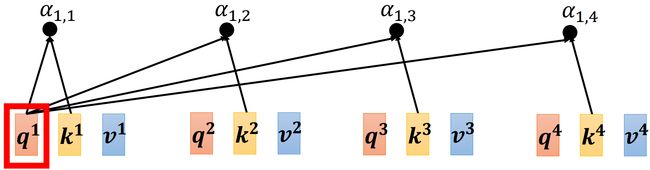
在实际操作中,我们也需要计算 α 1 , 1 \alpha_{1,1} α1,1,也就是 q 1 {\bf q}^1 q1 和 k 1 {\bf k}^1 k1 都由 a 1 {\bf a}^1 a1 分别乘上矩阵 W q , W k {\rm W}^q,\ {\rm W}^k Wq, Wk 得到(需要计算自己和自己的相关性),其余的 α \alpha α 计算方式同上。最后通过 s o f t m a x softmax softmax 得到 α 1 , i ′ \alpha_{1,i}' α1,i′,即 α 1 , i ′ = exp ( α 1 , i ) / ∑ j exp ( α 1 , j ) \alpha_{1,i}'=\exp(\alpha_{1,i})/\sum_j\exp(\alpha_{1,j}) α1,i′=exp(α1,i)/∑jexp(α1,j)。
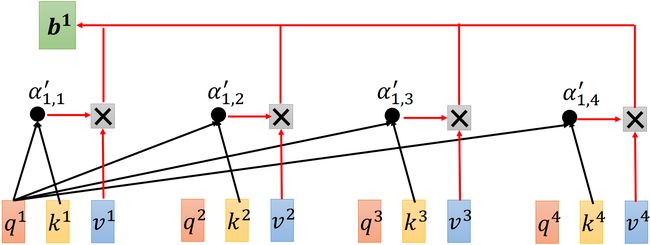
得到 α 1 , i ′ \alpha_{1,i}' α1,i′ 后,我们需要根据 α 1 , i ′ \alpha_{1,i}' α1,i′ 来抽取出 sequence 中重要的信息。如下图所示,对于每个 a {\bf a} a 都乘上矩阵 W v {\rm W}^v Wv 得到向量 v {\bf v} v;接下来,用 attention score 乘上每个 v {\bf v} v 再求和就得到了 b 1 {\bf b}^1 b1,即 b 1 = ∑ i α 1 , i ′ v i {\bf b}^1=\sum_{i}\alpha_{1,i}'{\bf v}^i b1=∑iα1,i′vi。哪一个 α 1 , i ′ \alpha_{1,i}' α1,i′ 大,那么 b \bf b b 就会越接近该 v \bf v v 向量。

计算 b 2 {\bf b}^2 b2 的过程也类似, b 2 = ∑ i α 2 , i ′ v i {\bf b}^2=\sum_{i}\alpha_{2,i}'{\bf v}^i b2=∑iα2,i′vi。总之,要计算 b i {\bf b}^i bi,首先,由 a i {\bf a}^i ai 和矩阵 W q , W k , W v {\rm W}^q,\ {\rm W}^k,\ {\rm W}^v Wq, Wk, Wv 计算 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi;再由 q i , k j {\bf q}^i,\ {\bf k}^j qi, kj 计算出 α i , j \alpha_{i,j} αi,j,再通过 s o f t m a x softmax softmax 得到 α i , j ′ \alpha'_{i,j} αi,j′(attention score);最后得到 b i = ∑ j α i , j ′ v j {\bf b}^i=\sum_j\alpha'_{i,j} {\bf v}_j bi=∑jαi,j′vj。

Self-attention in the view of matrix multiplication
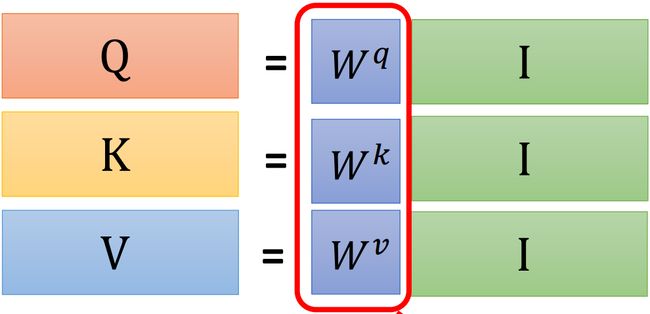
Step 1: 计算 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi

我们已经知道了需要 a i {\bf a}^i ai 和矩阵 W q , W k , W v {\rm W}^q,\ {\rm W}^k,\ {\rm W}^v Wq, Wk, Wv 计算 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi。接下来通过矩阵乘法的角度来看self-attention。

如上图所示,我们可以将 a i {\bf a}^i ai 拼接起来记作 I {\bf I} I(input),因此与矩阵 W q , W k , W v {\rm W}^q,\ {\rm W}^k,\ {\rm W}^v Wq, Wk, Wv 作矩阵乘法得到 Q , K , V {\bf Q},\ {\bf K},\ {\bf V} Q, K, V(分别是 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi 拼接的结果)。
Step 2: 计算 α \alpha α

我们已经知道了 attention score 的计算方式,如上图所示, α 1 , i \alpha_{1,i} α1,i 由 q 1 {\bf q}^1 q1 和 k i {\bf k}^i ki 做内积得到。还是通过矩阵乘法的角度,上述的过程可以看作:

继续扩展:

attention score 的矩阵 A {\bf A} A 是由 K T , Q {\bf K}^{\rm T},\ {\bf Q} KT, Q 做矩阵乘法得到,即 A = K T Q {\bf A}={\bf K}^{\rm T}{\bf Q} A=KTQ;attention score 再标准化一下(这里选择 s o f t m a x softmax softmax)得到矩阵 A ′ {\bf A}' A′(attention matrix)。
Step 3: 计算 b i {\bf b}^i bi
如上图所示,我们已经知道了 b i = ∑ j α i , j ′ v j {\bf b}^i=\sum_j\alpha'_{i,j} {\bf v}_j bi=∑jαi,j′vj,接下来用矩阵乘法的角度来看这一过程。
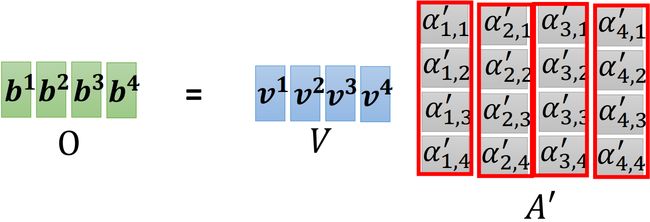
如上图所示,利用矩阵乘法得到 b i {\bf b}^i bi 组成的矩阵 O {\bf O} O(output),也就是 self-attention 最终的输出。
Brief Summary
计算 q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi:
计算 α \alpha α:

计算 b i {\bf b}^i bi:

虽然 self-attention 这一系列操作做下来会有些复杂,但仅有矩阵 W q , W k , W v {\rm W}^q,\ {\rm W}^k,\ {\rm W}^v Wq, Wk, Wv 是需要训练学习到的参数。
Multi-head Self-attention
在翻译、语音识别,利用 multi-head 可能会有较好的结果。为什么需要 multi-head?在做 self-attention 的时候,我们在用 q {\bf q} q 去找相关的 k {\bf k} k,而向相关的种类有很多种,因此我们需要不同的 q {\bf q} q 负责不同种类的相关性。

以 2 2 2 头为例, q i , k i , v i {\bf q}^i,\ {\bf k}^i, {\bf v}^i qi, ki,vi 分别乘上两个矩阵得到 q i , 1 , q i , 2 ; k i , 1 , k i , 2 , v i , 1 , v i , 2 {\bf q}^{i,1},\ {\bf q}^{i,2};\ {\bf k}^{i,1},\ {\bf k}^{i,2},\ {\bf v}^{i,1},\ {\bf v}^{i,2} qi,1, qi,2; ki,1, ki,2, vi,1, vi,2。计算 self-attention 的步骤类似,但多头之间的计算仅涉及一类。如上图所示,计算 b i , 1 {\bf b}^{i,1} bi,1,首先分别计算出 q i , 1 {\bf q}^{i,1} qi,1 与 k i , 1 {\bf k}^{i,1} ki,1 和 k j , 1 {\bf k}^{j,1} kj,1 的 attention score,接下来将这两个 attention score 分别乘上 v i , 1 , v j , 1 {\bf v}^{i,1},\ {\bf v}^{j,1} vi,1, vj,1 再进行 weighted sum \text{weighted sum} weighted sum 到一起就是 b i , 1 {\bf b}^{i,1} bi,1。
类似地, q i , 2 {\bf q}^{i,2} qi,2 只会和 k i , 2 , k j , 2 , v i , 2 , v j , 2 {\bf k}^{i,2},\ {\bf k}^{j,2},\ {\bf v}^{i,2},\ {\bf v}^{j,2} ki,2, kj,2, vi,2, vj,2 进行计算得到 b i , 2 {\bf b}^{i,2} bi,2。如果有更多的头,顺推即可。
当得到 b i , 1 , b i , 2 {\bf b}^{i,1},\ {\bf b}^{i,2} bi,1, bi,2 后,可以将它们拼在一起,再乘上一个矩阵(进行 transform)就可以传到网络的下一层:

Positional Encoding
在 self-attention 的操作中,忽略掉了位置信息;(每一个 input 出现在最前面还是最后面是不知道的)—— 引入 Positional Encoding 技术。
为每一个位置都设置一个唯一的位置向量(positional vector) e i , i means position e^i,\ \text{i means position} ei, i means position,一种做法是将 e i e^i ei 加到输入 a i a^i ai 上:
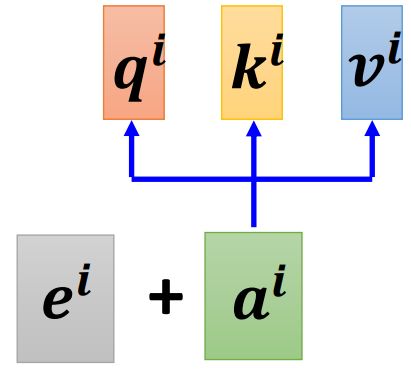
e i e^i ei 的可能取值(Attention is all you need):

Applications of self-attention
NLP

Speech
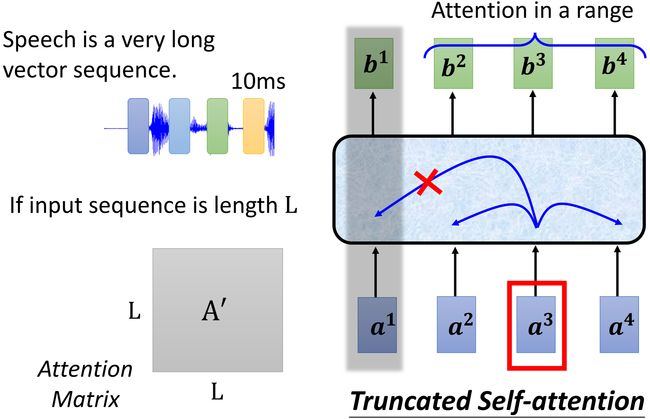
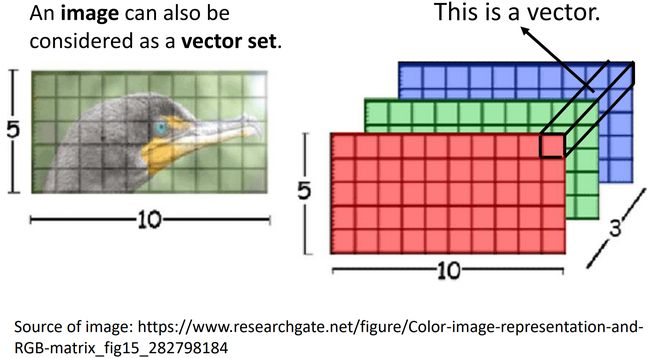
Image

Self-attention v.s. CNN


On the Relationship between Self-Attention and Convolutional Layers

An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale