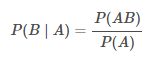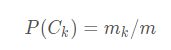机器学习之朴素贝叶斯算法
引言: 很多机器学习算法都从误差角度来构建模型函数f,也就是减少损失函数。而贝叶斯算法则是从概率的角度来考虑。贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
1 分类问题综述
对于分类问题,其实谁都不会陌生,日常生活中我们每天都进行着分类过程。例如,当你看到一个人,你的脑子下意识判断他是学生还是社会上的人;你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱”之类的话,其实这就是一种分类操作。
既然是贝叶斯分类算法,那么分类的数学描述又是什么呢?
数学角度分析:
已知m个样本![]() x是特征变量,y是对应的类别。
x是特征变量,y是对应的类别。
要求一个模型函数h,对于新的样本x,能够尽量准确的预测出 y=h(x)
概率角度分析:
试想一个样本x,在可以的情况下,你可以求出它属于各分类的概率,即P(y1∣x),P(y2∣x),......P(yn∣x),其中有最大值的
P(ym|x),x即属于该分类ym。
其中Y叫做类别集合,其中每一个元素是一个类别,而X叫做项集合(特征集合),其中每一个元素是一个待分类项,f叫做分类器。分类算法的任务就是构造分类器f。
分类算法的内容是要求给定特征,让我们得出类别,这也是所有分类问题的关键。那么如何由指定特征,得到我们最终的类别,也是我们下面要讲的。
2 朴素贝叶斯分类
那么既然是朴素贝叶斯分类算法,它的核心算法又是什么呢?
是下面这个贝叶斯公式:
![]()
贝叶斯公式推导:
上面提到了条件概率的基本概念,那么当知道事件 B 发生的情况下事件 A 发生的概率 P(A∣B),如何求 P(B∣A) 呢?贝叶斯定理应运而生。根据条件概率公式可以得到:
而同样通过条件概率公式可以得到:
将 (2) 式带入 (1) 式便可得到完整的贝叶斯定理:
换个表达形式就会明朗很多,如下:
![]()
朴素贝叶斯算法描述
第 1 步:设 X={a1,a2,a3,…,an} 为预测数据,其中 ai是预测数据的特征值。
第 2 步:设 Y={y1,y2,y3,…,ym} 为类别集合。
第 3 步:计算 P(y1∣x), P(y2∣x), P(y3∣x), ……, P(ym∣x)。
第 4 步:寻找 P(y1∣x),P(y2∣x),P(y3∣x),…,P(ym∣x) 中最大的概率 P(yk∣x) ,则 x 属于类别 yk。
3 例题分析
下面我先给出例子问题。
给定数据如下:
![]()
现在给我们的问题是,如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
![]()
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量.
p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
4 朴素贝叶斯算法的朴素一词解释
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!
对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
但是为什么需要假设特征之间相互独立呢?
1、我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
2、假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),
我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
好的,上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解!
我们将上面公式整理一下如下:
![]()
下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
5.贝叶斯算法python实现
6.贝叶斯算法拓展分析
参数估计
用频率来估算概率,统计m个样本中属于 Ck的样本的频率即可。设m个样本中有mk个样本的类别是Ck.则:
计算需要事先假设样本特征xj的数据分布情况。对特征分布的假设,我们称之为事件模型,通常会采用以下三种假设。
- 多项式分布
- 伯努利分布
如果特征xj 是稀疏二项离散值,可以假设它符合 伯努利分布。
另外注意到伯努利分布其实是多项式分布的特例。
- 高斯分布
优缺点
朴素贝叶斯的主要优点有:
1)算法简单,有稳定的分类效率。
2)对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
3)对缺失数据不太敏感。朴素贝叶斯的主要缺点有:
1)“朴素”的假设如果与实际情况不符,会影响模型效果。
2)输入特征数据的表现形式,比如是连续特征,离散特征还是二元特征,会影响概率计算和模型的分类效果。
转载自:https://blog.csdn.net/amds123/article/details/70173402
https://blog.csdn.net/x_iunknown/article/details/82898503