机器学习：KNN算法对鸢尾花进行分类

机器学习：KNN算法对鸢尾花进行分类

1.KNN算法的理解：

1.算法概述

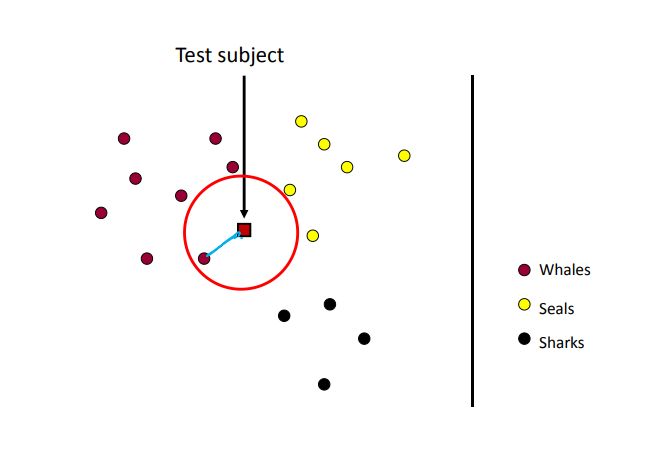
KNN（K-NearestNeighbor）算法经常用来解决分类与回归问题， KNN算法的原理可以总结为"近朱者赤近墨者黑"，通过数据之间的相似度进行分类。就是通过计算测试数据和已知数据之间的距离来进行分类。

如上图，四边形代表测试数据，原型表示已知数据，与测试数据最近的一个已知数据为红色的’whale’，所以对这个测试数据的预测值也为’whale’,这是取k值为一的情况，k表示要取最近的k个已知数据进行预测。k取大于一时则以占比较多的那类数据为预测结果，通常k值不等于一，容易产生过拟合的情况。

算法流程：

1. 计算预测数据与训练数据的距离
2. 选择距离最小的前K个数据
3. 确定前K个数据的类别，及其出现频率
4. 返回前K个数据中频率最高的类别（预测结果）

2.算法难点

KNN算法的难点在于距离计算以及k值的确定

距离计算：

测试数据与训练数据的距离计算方法有很多种，可以用如曼哈顿距离，欧式距离，余弦距离等。在KNN算法中常使用的距离计算方式是欧式距离，计算公式如下

确定k值：

K值选择问题，李航博士的一书「统计学习方法」上所说：

1. 选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

2. 选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

3. K=N（N为训练样本个数），则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的K值。

总结：

• K值较小，则模型复杂度较高，容易发生过拟合，学习的估计误差会增大，预测结果对近邻的实例点非常敏感。
• K值较大可以减少学习的估计误差，但是学习的近似误差会增大，与输入实例较远的训练实例也会对预测起作用，使预测发生错误，k值增大模型的复杂度会下降。
• 在应用中，k值一般取一个比较小的值，通常采用交叉验证法来来选取最优的K值。

2.sklearn的iris数据集介绍

Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性

iris以鸢尾花的特征作为数据来源，常用在分类操作中。该数据集由3种不同类型的鸢尾花的50个样本数据构成。其中的一个种类与另外两个种类是线性可分离的，后两个种类是非线性可分离的。

四个属性：
Sepal.Length（花萼长度），单位是cm;
Sepal.Width（花萼宽度），单位是cm;
Petal.Length（花瓣长度），单位是cm;
Petal.Width（花瓣宽度），单位是cm;

查看数据集：

from sklearn.datasets import load_iris

if __name__=='__main__':
    #鸢尾花数据集
    datas = load_iris()
    print(datas)

sklearn的其他数据集可见：

sklearn提供的自带的数据集 - nolonely - 博客园 (cnblogs.com)

3.使用sklearn库实现KNN算法对iris数据集的分类

载入数据集并划分训练与测试集：

iris = datasets.load_iris()

feature = iris['data']  
target = iris['target']  

x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2022)

# print(x_train)  

定义k值并对比测试集的测试结果，查看准确率

knn = KNeighborsClassifier(n_neighbors=3) 

train = knn.fit(x_train, y_train)
#print(knn)  

y_pred = knn.predict(x_test)
y_true = y_test

print('模型的分类结果:', y_pred)
print('真实的分类结果:', y_true)

print(knn.score(x_test, y_test))

完整代码：

import sklearn.datasets as datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()

feature = iris['data']  
target = iris['target']  

x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2022)#8：2划分数据集

# print(x_train)  

knn = KNeighborsClassifier(n_neighbors=3) 

train = knn.fit(x_train, y_train)
#print(knn)  

y_pred = knn.predict(x_test)
y_true = y_test

print('模型的分类结果:', y_pred)
print('真实的分类结果:', y_true)

print(knn.score(x_test, y_test))

test1 = knn.predict([[6.6, 3.1, 4.7, 2.6]])#测试
print(test1)

结果

K=3：

K=20：

K=100：

在三个k值中k=20时分类效果最好

（可以使用交叉验证来求最佳的k值，参考博客：史上最全KNN_knn数据集 ）

讨论：

KNN算法的优缺点：

优点：
1.理论简单，容易实现，既可以分类也可以回归；

2.精度高，对异常值不敏感，几个异常值无关大碍；

3.新数据可以直接加入数据集而不必进行重新训练。

缺点：
1.分类计算量大时，内存开销大，必须保存全部数据集，即空间复杂度高；

2.无法给出基础结构信息，无法知晓平均实例样本与典型实例样本具有什么特征，即无法给出数据的内在含义（决策树），可解释性差；

3.对于稀疏数据集束手无策，要求样本数据平衡，否则预测偏差比较大。

4.只适用于监督学习，就标签表明种类。