吴恩达机器学习--学习笔记

1. Introduction

1.1 Welcome

如今机器学习被大规模应用于：

• 数据挖掘（网站点击，医学记录，生物学，工程）
• 一些无法通过编程实现的功能（自动驾驶，手写识别，NLP，CV）
• self-customizing programs（各种网站的推荐系统）
• 辅助理解人脑

这是一个快速发展的领域，我看好

1.2 What is machine learning

常用的机器学习包括监督学习算法和无监督学习算法。
此外还有增强学习和推荐系统。

1.3 Supervised Learning

监督学习的样本是带有标签的（即我们知道预测所对应的真实值是多少）。

1.4 Unsupervised Learning

无监督学习的样本是没有标签的（即我们不知道真实值）。

2. Linear Regression with one variable

2.1 Model Representation

h = theta`x

2.2 Cost Function

线性回归的J采用了平方误差公式（squared error function)

2.3 Cost Function - Introduce I

代价函数J衡量了训练样本的预测值与真实值之间的整体误差。当拟合的越差的时候，J越大，也就是代价越高。那么通过找到令J最小的theta，也就找到了对训练样本集最好的拟合。

2.4 Cost Function - Introduce II

…

2.5 Gradient Descent

梯度下降法是一种用来找到J最小值的常用方法。其实它的思路非常简单，我们不断迭代，每次迭代令J向减小最快的方向（即梯度方向）移动，直到找到一个最小值（这个值可能是局部最小值）。

在梯度下降法的初始位置不同时，最后可能获得不同的最小值。

在实现梯度下降法时，应该同时更新每个theta的分量（否则就不是向着梯度的方向移动）。

2.6 Gradient Descent Intuition

在实现梯度下降法时，选取学习速率alpha是个技术活。alpha太小，则求解太慢。alpha太大，则可能造成发散（当由于alpha过大造成我们超过最小点时，新的位置的梯度如果更大，则会再次越过最小点，并往复下去，造成发散）。

尝试不同的alpha值，并画出相应的学习曲线选择合适的alpha的一种方法。一般采用3倍的方式选择alpha，比如0.3, 0.1, 0.03, 0.01

一个固定的alpha也可以让梯度下降法收敛于最小值，原因是随着位置趋近于最小值，梯度也趋近于0。

2.7 Gradient Descent for Linear Regression

线性回归的J是一个bowl shaped图形（弓形），更正式的名字是convex function（凸函数）。这种形状只有一个全局最优解，没有局部最优解。所以通过梯度下降法我们总是可以收敛到全局最优解。

到此位置我们所使用的Gradient Descent其实有一个更准确的名字–Batch Gradient Descent（批量梯度下降）。批量的意思是，每次迭代，我们都考虑所有样本的影响。

2.8 What`s next

接下来会复习下线性代数，因为线性代数非常适合处理机器学习中的大量参数问题。

3. Linear Algebra Review

3.1 Matrices and Vectors

3.2 Addition and Scalar Multiplication

3.3 Matrix Vector Multiplication

3.4 Matrix Matrix Multiplication

3.5 Matrix Multiplication Properties

A * B not eq B * A
A * B * C = A * (B * C)
A * I = I * A = A

3.6 Inverse and Transpose

只有方阵才可能有逆矩阵（换句话来说，有逆矩阵的矩阵一定是一个方阵）。

没有逆矩阵的矩阵叫做奇异矩阵或者退化矩阵。

4. Linear regression with multiple variables

4.1 Multiple features

4.2 Gradient Descent for Multiple Variables

4.3 Gradient descent in practice I: Feature Scaling

在应用梯度下降法时，我们需要先观察下各个特征的取值范围。如果各个特征的取值范围差距很大，会造成梯度下降法收敛很慢。这时候就需要对特征作缩放。

特征缩放的目的是将各个特征的取值范围映射到[-1,1]。不过也不是非得在这个区间合理。按照吴恩大的经验，[3,3]和[-1/3,1/3]这样的区间都是合理的。

特征缩放常采用如下方式映射：
x = x / x_max
这样就映射到了[-1,1]

其实更常规的方式是均值归一化（mean normalization）
x = （x - mu） / theta
这样就映射到[-0.5, 0.5]

4.4 Gradient descent in practice II: Learning Rate

选择一个合适的的学习速率是个技术活，一般按照X3的规律来选，例如：0.001，0.003，0.01，0.03，0.1 …

太小的alpha会导致收敛太慢
太大的alpha则有可能导致完全不收敛

那么如何来确认当前算法通过迭代有收敛呢？即如何来debug呢？

那就是画学习曲线。通过观察学习曲线我们可以确定算法在迭代后是否有收敛。同时也可以用来选择一个合适的学习速率。

当然也不是没有自动确认是否收敛的方法。那就是通过check每次J的变化量。如果变化量已经小于一个很小的值（比如1e-3），则认定当前算法已经收敛。但这个最小值的选择就有点困难了。

4.5 Features and Polynomial Regression

当处理多特征的回归时，我们面临一个问题----特征选择，即采用哪些特征，我们甚至可以由原特征创造新的特征来进行回归。
多项式回归就是源于这种思想。通过将各种特征组合，我们可以创造新的特征，并更好的拟合数据。

4.6 Normal Equation 标准方程法

在求解线性回归的参数时，除了梯度下降法，标准方程法是另外一种选择。而且相对于梯度下降法，标准方程法还有一些优点，比如

• 不需要设置alpha
• 不需要作均值归一化

但是它也有局限。当特征数n比较大时（比如大约1e4），标准方程法的计算会变得很慢（标准方程法的计算量是O(n^3))，而此时就不得不采用梯度下降法。

按照吴恩达的经验，1e4就是这个选择的分解点。

标准方程法的公式如下：
theta = ( X’X)inverse * X’ * y
其中X称作design matrix（即样本设计出来的矩阵）

4.7 Normal equation and non-invertibility

如果X‘X不可逆怎么办呢？

首先这种情况极少发生。
其次假设这种方法发生了，它通常可能是由于存在重复的特征（如倍数关系的特征），对于这种情况删除冗余特征就可以了。另外导致不可逆的原因也可能是因为m < n，即相对于样本数特征数太多了，这时可以删除一些特征或进行正则化处理。

在使用octave时，即使X‘X不可逆，pinv()的计算结果也是正确的。所以不可逆的为难题无需特别关注。

5. Octave Tutorial

5.1 Basic Operations

不等于的符号有点特殊 ～=
XOR 异或
disp 命令可以输出一些复杂的输出，比如
disp(sprintf(‘2 decimals: %0.2f’, a))

控制长短的命令：
format long
format short

矩阵和向量赋值：
；代表在矩阵中换行

1：6 % 1 2 3 4 5 6
1： 0.1 : 6 % 1 1.1 1.2 … 5.9 6

ones(2,3)
1 1 1
1 1 1

2*ones(2,3)
rand(3,3)
randn(1,3) % 高斯分布

hist()
eye(3)
1 0 0
0 1 0
0 0 1

5.2 Moving Data Around

size(A) % 例如1 2，说明A是一个1X2的矩阵
length(A) % 返回A最大维的长度
load .dat
load(’.dat’)
who % 显示当前工作空间所有变量
whos % 更详细的现实
clear * % 清除特定变量
clear % 清除所有变量
save *.mat v % 将变量v存储为一个mat文件（二进制的）
save hello.txt v - ascii % 存储为一个txt文件
A(3,2)
A(2,:)
A([1,3],: )
A( : ) % 所有元素输出为一个列向量
A = [ A B]
A = [ A ; B]

5.3 Computing on Data

A*B % 矩阵乘法
A.*B % 对应元素乘法
A+1 % 每个元素+1
A‘ % 转置

a= [ 1 15 2 0.5]
max(a) % 15
[val,ind] = max(a)
a<3 % 1 0 1 1
find(a<3) % 1 3 4
magic()

sum() % 求和
prod() % 去累乘

floor() %0.5 --> 0
ceil() % 0.5–> 1

max(A) % 每列最大值
max(A,[],1) % 每列最大值
max(A,[],2) % 每行最大值

max(max(A))
max(A(: ))

sum(A,1) % 每一列的总和
sum(A,2) % 每一行的总和

pinv(A) % 求伪逆

5.4 Plotting Data

plot()
xlabel()
ylabel()
legend()
title()
subplot()
axis()
print -dpng ‘myplot.png’
imagesc(A) % 图像化矩阵
colorbar
colormap gray

5.5 Control Statements

5.6 Vectorization

5.7 Working on and Submitting Programming Exercises

Programming Exercise 1: Linear Regression

在第一次课后练习中，吴恩达安排我们对近来学习的内容进行了一次实践。这包括线性回归和数据可视化的相关内容。

在实践线性回归时，我们需要进行数据的读取，均值归一化（单变量情况不需要），代价函数的计算，以及通过梯度下降法求解系数。当然我们也可以采用正则方程的方式来求解系数，在n较小时（比如<1000）这是一种不错选择，因为不再需要迭代和均值归一化。

最后，我们还画出了各种不同的学习速率时梯度下降法的学习曲线。这可以帮助我们选择一个合适的学习速率。

6. Logistic Regression

6.1 Classification

我们可否用之前学习的线性回归来处理分类问题呢？大部分情况下，这不是一个好主意。为什么呢？假设我们用线性回归对样本集合进行拟合，并很好的将两个分类分开。这时候如果在样本集中增加一个远偏离其他样本的点，这会让线性回归的曲线大幅度偏移，进而造成线性回归的曲线不再能够很好的对样本集进行分类。其次，线性回归也无法满足y属于[0,1]的要求。

6.2 Hypothesis Representation

Logistic回归的表达式通过S函数是将线性回归的预测值映射到（0，1）之间。所以我理解Logistic回归是演变的线性回归。

6.3 Decision Boundary

决策边界是什么呢？简单点说，就是一条将不同分类的样本分割的线。这条线由hypothesis的参数决定，线的两侧预测值不同。

6.4 Cost Function

Logistic回归不用沿用线性回归的J，原因是S函数的引入造成J非凸，这样就无法通过梯度下降法收敛到最小值。

6.5 Simplified Cost Function and Gradient Descents

6.6 Advanced Optimization

在实际的操作过程中，我们可以采用一些库提供的高级优化算法来求解参数的估计，这会比梯度下降法快的多，而且还不用选择学习速率alpha。这些算法包括：Conjugate gradient, BFGS, L-BFGS等等。幸运的是Octave提供了这些库，我们只需要提供计算J和J的梯度的计算函数就可以利用这些算法来实现高效计算。

6.7 Multiclass Classification One-vs-All

如何将Logistic回归扩展到多分类问题中呢？很简单，对于多分类问题中的每个分类都建立一个1 vs others的Logistic回归，对于测试样本，预测值最大的对应的分类就是预测结果。

7. Regularization 正则化

7.1 The Problem Of Overfitting

当我们的选用了过多的变量来进行预测时可能造成模型过拟合。过拟合，即采用很多变量来对训练样本进行拟合并且效果很好，但是对于测试样本却不好。
我们可以采用如下的方法来解决过拟合的问题：

• 手动选择部分变量
• 通过模型选择来选择部分变量
• 正则化，即保留所有的变量，但是令每个变量对应的参数都很小，这样每个变量对于预测的影响都不大，这样也可以解决过拟合

7.2 Cost Function

正则化是如何实现的呢？正则化在原始J后面增加一个参数值的惩罚项，即当theta的平方和较大的时候J也会变得较大，这样参数估计就会趋向于一个theta较小的结果。
如果惩罚项的lamda过大时会怎么样呢？这时候所有theta都会趋向于0，会造成严重的欠拟合。

7.3 Regularized Linear Regression

在通过梯度下降法求解正则化的线性回归时，你会发现相对于原始的线性回归，正则化其实令theta在每次迭代的时候首先乘以了一个小于1的正数，这样就令theta逐渐变成一个较小的数。
此外当采用标准方程来求解正则化的线性回归时，正则化还保证了可逆性。

7.4 Regularized Logistic Regression

Programming Exercise 2: Logistic Regression

8. Neural Networks Representation

8.1 Non-linear hypotheses

既然我们可以通过多项式来分类，为什么还需要神经网络呢？那是因为，多项式有一个很严重的问题，就是随着特征数的增多，多项式的复杂度会不可承受。

8.2 Neurons and the Brain

8.3 Model Representation I

8.4 Model Representation II

通过前向传播我们可以把神经网络的架构进行项量化表达。

8.5 Example and Intuition I

8.6 Example and Intuition II

8.7 Multiclass Classification

相对于二分类，多分类神经网络只是在输出层有多个神经元。

Programming Exercise 3: Multi-class Classification and Neural Networks

第二次实践涵盖了Logistic多分类以及神经网络的前向传播。从效果上看，神经网络确实更强大。

9. Neural Network Learning

9.1 Cost Function

由于神经网络的神经元是由Logistic函数构成的，所以神经网络的代价函数也是Logistic回归的代价函数的一个特殊形式，即对所有K个输出层单元的代价函数进行累加，并对所有层中的各个theta进行正则化处理。

9.2 Backpropagation Algorithm

神经网络通过反向传播算法来计算偏导数。

9.3 Backpropagation Intuition

反向传播算法真的很难懂。

9.4 Implementation Note Unrolling Parameters

由于优化算法通常要求参数以长向量的形式输入输出，所以需要利用reshape将参数矩阵和长向量进行转化。

9.5 Gradient Checking

神经网络的计算如此复杂，我们如何保证计算的准确性呢？
方法是通过梯度检查。思路其实很简单，即将梯度估计（可以通过直线斜率来估计曲线梯度）的值与方向传播的计算结果进行比较。如果差距很小，则证明准确。

9.6 Random Initialization

在利用优化算法前，我们需要对theta进行初始化。对于Logistic回归只需要进行0初始化，但对于神经网络则不能这么简单的初始化，因为这回造成权重对称问题，进而导致所有的隐藏层神经单元计算结果都一样。为了打破权重对称，我们需要对theta进行随机初始化。

9.7 Putting It Together

训练神经网络的大致流程是：

• 循环便利所有样本，通过前向传播和后向传播，计算DELTA矩阵
• 通过DELTA矩阵计算偏微分
• 通过梯度检查核实正确性
• 关掉梯度检查训练模型

9.8 Autonomous Driving

Programming Exercise 4: Neural Networks Learning

神经网络训练的实践。

10. Advice for applying machine learning

10.1 Decide What to Try Next

在讲一个机器学习模型应用实际时，我们可能会发现很大的误差。如何来减少误差呢？你可以会做如下的尝试：

• 获取更多的样本
• 使用更小的特征集
• 使用额外的特征
• 增加多项式特征
• 减小lambda
• 增大lambda
  但是到底什么样的努力才是有用的呢？做无用的尝试可能会耗费大量的时间，这些时间可能至少要几个月。这时候就需要通过机械学习诊断了（machine learning diagnostic）来获知什么努力可以提高模型的准确性。

10.2 Evaluating a Hypothesis

如何来评价一个模型呢？一种办法是将样本集按照7-3比例随机的分成训练集和测试集。这样我们就可以利用测试集来计算模型的J（对于分类问题，我们还可以计算错误率），以此来评价模型。

10.3 Model Selection and Train_Validation_Test Sets

有没有什么办法可以帮助我们选择更好的模型呢？比如在使用多项式模型时，多少纬度的多项式更好呢？这时候我们可以利用模型选择。
在进行模型选择时，我们将样本集按照6-2-2比例随机分成训练集/交叉验证集（CV）和测试集。我们利用训练集来训练各个模型，利用CV来选择误差最小的模型，最后在利用测试集来估计所选模型的范化误差。

为什么我们需要增加一个CV呢？
这是因为模型的选择也是一个拟合过程。如果我们用测试集来选择模型，然后又用同样的测试集来估计范化误差，那么一定是不准确的。

10.4 Diagnosing Bias vs. Variance

我们知道，模型的误差是由高偏差以及高方差导致的。所以，对模型进行诊断最重要的是要确定模型是处于高偏差还是高方差状态。

• 高偏差状态：此时高偏差是导致模型误差的主要原因，所以Jtrain和Jcv都会比较大。
• 高方差状态：此时高方差是导致模型误差的主要原因，所以Jtrain会比较小，Jcv还会比较大。
• 低误差状态：Jcv较小，这时候就完美了。

10.5 Regularization and Bias_Variance

正则化系数和偏差方差是什么关系呢？

• 正则化系数过大：此时估计的theta会太小，导致高偏差的问题
• 正则化系数过小：此时会严格拟合训练集，导致高方差的问题
• 正则化系数刚好：此时Jcv最小

即然选择不合适正则化系数会导致Jcv较大，那么如何选择合适的正则化系数呢？
方法仍旧是采用模型选择。即利用训练集对一系列lambda进行训练（比如0 0.01 0.02 0.04 0.08…10，吴恩达通常采用2倍递增），然后利用CV选择合适的lambda，最后用测试集评估性能。

10.6 Learning Curves

学习曲线是一个更强大的模型诊断的工具。我们人为对训练集进行处理，利用m递增的训练集来训练模型，计算Jtrain和Jcv，并将Jtrain和Jcv关于m的曲线画在一起—这就是学习曲线。通过观察学习曲线我们就可以对当前模型进行诊断。

• 高偏差状态：Jtrain和Jcv靠的很近，此时Jtrain是导致Jcv的主要原因，增加训练样本也无法明显优化模型。
• 高方差状态：Jtrain和Jcv间存在较大间隔，此时高方差是导致Jcv的主要原因，增加训练样本可以进一步优化模型。
  所以，画学习曲线是个好主意。

10.7 Deciding What to Do Next Revisited

Programming Exercise 5:Regularized Linear Regression and Bias Vs Varian

在画学习曲线时，尤其处理小样本集时，进行多次随机采样（如50）然后取误差的平均是一个很有效的方法。

11. Machine Learning System Design

11.1 Prioritizing What to Work On

在作机器学习系统设计时，首先应该列出可选的改进方案，而不是拍脑袋想到一个主意就去忙很久而最终证实这是无用功。

11.2 Error Analysis

当我们应用一个模型后，如何来进一步提高模型性能呢？
当然，我们应该利用学习曲线来作模型诊断。模型诊断可以帮助我们知道当前模型是处于高偏差还是高误差状态，给我们一个优化的大方向。但是具体应该怎么提高呢？比如增加新的特征。这时就要用到误差分析了。
以垃圾邮件识别为例。当我们发现有300多封没有正确识别出来的垃圾邮件时，我们也可以一封一封的去分析这些垃圾邮件，并将它们进行分类，以观察是那一类邮件更多的被错误分类。这样我们就知道在那一类垃圾邮件上花大力气优化。接下来，我们可以对邮件进一步分析，看什么原因导致邮件错误分类，进而确定通过什么手段（比如提取什么新的特征）来进步提升模型。
与此同时，我们需要量化指标（比如CV上的准确率或者错误率）来帮助我们确定新的尝试是否有益。

吴恩达建议，在遇到一个新的机器学习问题时，不要一开始就急于建立复杂的模型（因为你也不知道你尝试的方向是否正确，这些尝试完全是靠直觉），而应该尽快实现一个简单的模型，并确定性能量化的标准。此时你就可以作误差分析来寻找优化的方向，并通过量化标准来做选择。从而不断优化模型。

11.3 Error Metrics for Skewed Classes (12 min)

对于Skewed Class（即各分类的的样本占比差距巨大的分类问题），我们无法采用准确率来评判一个模型的好坏（比如癌症的例子，假如癌症患比只有0.5%，这时候我们只要设定一个模型将所有样本均判定为非癌症患者，就可以达到95.5%的准确率，但是显而易见这个模型是个垃圾模型）。

对于这种偏差分类，我们采用如下指标来衡量模型好坏：

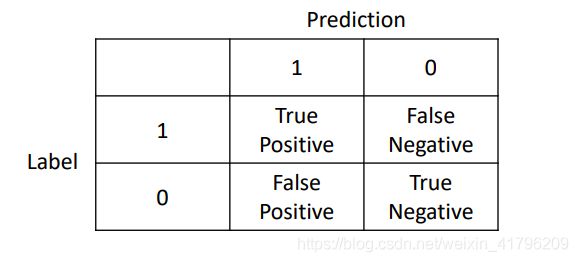
1. 查准率 precision – TP /（TP+FP）
2. 召回率 recall – TP / (TP+FN)

我们也可以通过画出混淆矩阵来更加直观的展现

11.4 Trading Off Precision and Recall

对于一个偏差分类，我们需要协调查准率和召回率来达到预期目的（比如癌症筛查的例子，是要更准确的预测–对应高查准率，还是要将更多的癌症患者查出来–对应高召回率）。

查准率和召回率往往是不可兼得的，除非非常理想的预测模型。

为了自动化选择查准率和召回率，我们用F score来综合考虑查准率和召回率。
Fscore = 2precisionrecall / (precision + recall)
从上面的公式可以看出，Fscore仅当precision和recall均等于1时才等于1，当precision和recall任意一个为0时都会是0（这就排除了对测样本全判1或者全判0的垃圾模型）。所以Fscore是precision和recall的综合考量。

我们可以按照如下步骤来自动选择查准率和召回率：

1. 按照不同的threshold计算Fscore
2. 自动选择Fscore最大时对应的查准率和召回率

11.5 Data for machine learning

大量的样本是否可以训练一个优秀的模型呢？这是有条件的

首先，每个样本必须有足够的特征来包含做预测所需要的信息，并且我们的模型可以充分利用这些特征。

其次，在满足上面一条后，大量样本的训练则可以造就一个优秀的模型。

丰富的特征及模型可以充分利用特征，保证了低偏差
大量的数据避免了过拟合，保证了低方差
低偏差和低方差的模型则是一个优秀的模型

但我们考虑是否可以通过搜集大量的数据来将一个模型训练成一个优秀的模型时，我们可以这样问自己

首先，利用当前特征集所包含的信息，一个人类专家是否有信息作出准确预测。

其次，我们是否有能力得到大量数据，并训练这个包含大量特征的模型。

如果这两条都可以，我们就可以得到一个优秀的模型。

12. Support Vector Machine

12.1 Optimization Objective

SVM某种意义上可以看成是Logistic的变种，SVM的优化目标即代价函数也可以看成是特殊的Logistic代价函数。

12.2 Large Margin Intuition

有时候，SVM会被称为一个大间距分类器。这是仅在C很大时才合理。当C很大时，SVM确实更像一个大间隔分类器，为了最小化代价函数，我们需要尽量将所有点正确分类。这时候一个outlier（异常点）就足以大幅影响决策边界，这是典型的过拟合。但是SVM可以通过调整C为一个相对较小的值，来允许一部分outlier错误分类，进行减小方差，提高分类器性能。由于参数C的存在，SVM得以可应用于非线性可分的场景。
所以SVM并非一个简单的大间距分类器。

12.3 Mathematics Behind Large Margin Classification (Optional)

通过之前的学习，我们知道，当C为一个很大的实数时，SVM的优化目标是在正确将样本分类的同时使得theta的范数尽量小。而大间距分类器会让各个样本在theta上的投影尽可能的大，这样就不要求theta的范数比较大，这与SVM的优化目标一致。反之，若分类边界两端的间隔较小，则各个样本在theta上的投影较小，要满足正确分类，则必须theta的范数较大。
宗上，通过求解优化目标，SVM最后会选择分类间距最大的大间距分类器。

12.4 Kernels I

对于线性不可分的情况，如何来选择一条非线性分类边界来进行分类呢。典型方法是采用多项式，但这会带来计算量大的问题。SVM作为一个线性分类器，配合核函数，也可以对线性不可分的情况进行分类。我理解核函数是一种映射函数，将样本映射到新的特征空间。本讲给出了一个应用例子：
首先，在原特征空间找到一些landmark
然后，通过高斯核函数计算各个样本与landmark的相似度（这里对应的是距离），并将这些相似度作为新的特征。
最后，在新的特征空间里，不同的分类会按与landmark的远近而分离为两类。这时候就可以通过SVM找到分隔超平面，将样本分类

理论上来讲，通过以上方法，只要我选择的landmark够多（甚至每个样本作为一个landmark），我可以将任何非线性可分的情况进行分类，但这样必然导致过拟合。

12.5 Kernels II

之前真没想到，landmark的选取方式还真是每个样本作为一个landmark。更没有想到的是，这样选择landmark本身并不会导致过拟合。因为每个样本的判定都要考虑所有的landmark，而并不是由个别landmark决定。
过拟合出现在参数选则不合理时，比如

1. 较大的C
2. 较小的sigma(当采用高斯核函数时）

12.6 Using An SVM

不同的场景如何选择logistic还是svm来创建function呢，不同情况选择不同：

• 对于特征数n很大，样本数m较小的时候，应该选用liner kernel（因为此时一个非线性的分类界面容易产生过拟合）
• 对于n较小，m又比较适中的时候，可以采用Gaussian kernel（但需要先将特征进行scaling）
• 对于n较小，m较大时，应该增加新的特征，然后应用logistic或者liner kernel的svm

以上各种场景，神经网络都可以适用，但是计算量太大了（在我看来神经网络是应对大特征量，大样本量的神器，例如图像识别中将每个像素点看成一个特征）。

很多场景下，logistic和liner kernel svm是可以同时胜任的。有时最终决定性能优劣的不是算法，而是谁的数据量大…

Programming Exercise 6: Support Vector Machines

本次实践首先演示如何通过SVM对线性可分的样本进行分类，然后利用径向基函数（高斯核函数）对线性不可分的样本进行分类，还演示了如何选取C和sigma。
在实践的最后是利用SVM实现了垃圾邮件识别。垃圾邮件分类一般是采用朴素贝叶斯来实现，但我们可以看到SVM同样达到了非常好的效果。SVM真是强大。

13. Clustering

13.1 Unsupervised Learning Introduction

终于到非监督学习了。第一个要介绍的非监督学习方法是聚类算法。

13.2 K-Means Algorithm

K Means可能是最常使用的非监督分类算法了。该算法实现起来也特别简单
首先，指定要分类的组数K，并随即制定K个点作为这K个分组的均值点。
然后，就反复进行“分类–更新均值点”，直到收敛（分类稳定，均值点不再改变）。
此时聚类就完成了。

对于在优化过程中没有样本的分类均值点，一般采用移除的操作。当然，如果目标是强制保证K个分类，这时也可以将均值点再次随即制定。

聚类算法不一定处理的都是些本来就可以很好聚类的样本的分类问题。有时候也可能用于强制将一些本来并不是分开的样本分成几个分类。

13.3 Optimization Objective

K Means的优化目标是所有样本与其所属分类的分类中心点距离平方均值最小。为了达到这个优化目标，K Means反复执行如下步骤：

1. 保持分类中心点不变，正确分类各样本点 — 即在分类中心不变情况下，优化J
2. 重新计算分类中心点 — 即在样本点分类不变的情况下，优化J

13.4 Random Initialization

执行K均值聚类前，需要选择初始的聚类中心点。这时建议采用随即初始化的方式，随即选择K个样本作为初值。
有时候，一次K均值聚类可能无法收敛到全局最优解（收敛到一个局部最优解）。这时如果K较小（比如2-10，可以采用多次（比如100次）执行K均值聚类（每次随即初始化聚类中心点）来选择J最小的解。
当K比较大的时候，这种方法就不管用了。因为此时随即初始化对于K很大的K均值聚类影响不大。

13.5 Choosing the Number of Clusters

如何来选择K Means中的K呢？通常没有一个通用的办法。有时可以采用肘部方法，也就是将一系列K值与对应的J画成一条曲线，取其中的折点。但某些时候，根本找不到这个折点。
更多时候，我们应该通过考虑聚类的目的来确定K值。即分成多少个类能够更好达到真正的目的（如潜在客户分类，商品型号分类等）。

14. Dimensionality Reduction

14.1 Motivation I : Data Compression

吴恩达从这一讲开始介绍另外一种无监督学习方法–降维。比如当前样本在二维特征空间，但是实际上所有样本均是在一条直线附近，那么完全可以用样本在当前直线上的投影位置来确定样本。这样就达到了降维。
降维的第一个好处就是可以减少空间，减小存储压力，同时也提高了算法处理速度。

但是这与无监督学习有什么关系啊？

14.2 Motivation II ： Visualization

通过降维，我们可以对数据在一个较小的纬度上进行可视化。这样就给数据分析提供了很大的便利。

14.3 Principal Component Analysis Problem Formulation

PCA（主成分分析）可能是最常用的降维方法。PCA通过将高维数据投影到低维空间，并最小化投影误差的平方来进行降维。

14.4 Principal Component Analysis Algorithm

PCA实现如下：

1. 对数据预处理，包括均值标准化和scaling（可选）
2. 计算协方差矩阵Sigma
3. 计算协方差矩阵的特征向量矩阵
4. 选取协方差矩阵中的前K个特征向量，并组成降维后的特征向量矩阵Ureduce
5. 用Ureduce来对各个样本作降维映射

通过以上步骤就实现了PCA（在降维的同时，最小化投影误差的平方）

14.5 Choosing the Number of Principal Components

如何为PCA选择一个合适的K呢？常规方式是从1开始遍历，找到最小的满足以下条件的K

• 投影误差平方均值 / Total Variance of the Data <= 0.01（也可能是0.05 0.1），这个条件代表虽然经过了降维，但是99%的variance还是被保留了下来

当然这样计算效率很低。更高效的方式是利用octave中svd函数输出的S矩阵来计算。

14.6 Reconstruction from Compressed Representation

降维后的数据是可以重建回原数据的。方法也非常简单。只需要用Ureduce*Z就可以得到X（因为Z=Ureduce`*X，而Ureduce又是由特征向量组成的）。只要投影误差的平方均值不是很大，又可以重建一个近似的原数据。

14.7 Advice for Applying PCA

PCA常被用来降低机器学习算法的存储压力或提高运行速度。但是除非这是必要的，否则并不建议滥用PCA（PCA作为一种无监督学习方法，不考虑y值，虽然可以保留99%的variance，但是还是会丢掉一部分信息）。
另外一种常见的滥用是利用PCA来防止过拟合（PCA减少了特征数量，可以减小过拟合的可能性）。但是相对于PCA，更推荐利用规则化来避免过拟合。

此外，在应用PCA的过程中，应该用train集来训练PCA，而不应该动用CV或者test集。

Programming Exercise 7:K-means Clustering and Principal ComponentAnalys

本次实践首先演示K均值聚类算法，并将其应用于图片压缩。可以看到利用K均值聚类算法可以实现对原图像6倍压缩的同时保留图像大部分的特征。
实践的第二部分演示PCA。首先演示如何通过PCA将一个2D的数据集映射到了一个1D的数据集。然后演示了如何通过PCA对人脸照片进行压缩。如果此时有一个基于神经网络的人脸识别算法，就可以将1024D的数据映射到100D来进行处理，大大提高运行速度的同时，还保留大部分的信息。实践在最后演示了PCA在数据可视化的应用—将一个3D的散点图映射到一个2D的散点图，这样在分析图形时就更直观了。

15. Anomaly Detection

15.1 Problem motivation

这一讲开始介绍一种新的无监督学习方法–异常检测。通过找出与大部分样本不一致的样本，来识别异常样本。背后的思路很简单，假如大量的样本都是正常的，那么从聚类上远离集体的样本就更有可能不正常。

这种方法被大量应用于欺诈识别，产品QA，计算机集群监控等领域。

那么，异常检测学习算法是怎么实现的呢？

实际上它是通过密度估计来做到这一点的。即对样本属于正常样本的概率进行建模，通过p(x)来判断样本份分类。

那p(x)又是如何被估计出来的呢？

这里建立在x符合高斯分布这一假设前提下，这样我们就可以通过大量的样本估计高斯分布的mu和sigma。

15.2 Gaussian Distribution

这一讲简要介绍了高斯分布。同时也介绍了对均值和方差的参数估计（即通过样本估计分布的参数）。这里采用了极大似然估计（即对于当前的样本，使当前样本出现的概率最大的参数，就是我们得到的估计值）。

15.3 Algorithm

异常检测的算法细节是什么样的呢？

异常检测假设样本的各特征之间独立并且符合高斯分布。基于这样的假设，我们就可以通过样本对各个特征的分布的参数进行估计，并利用估计后的结果计算测试样本的p(x)，从而判断一个样本是否属于异常点。

15.4 Developing and Evaluating an Anomaly Detection System

如何开发一个异常检测学习算法呢?如何来评价其性能好坏呢？

开发异常检测学习算法：

1. 首先将样本划分为train/cv/test三个集，并假定train中所有样本都是normal的（其实即使有少量异常样本也无妨），假定cv和test是有label的，并且包含部分异常样本
2. 用train set来训练异常检测算法
3. 用cv来选择epsilon和特征集（由于异常检测所应用的样本集应该是一个倾斜集合，所以准确率在这里并不适用，我们采用查准率，召回率，F1scre来选择epsilon和特征）
4. 用test来评价算法性能

15.5 Anomaly Detection vs. Supervised Learning

我们看到，异常检测的训练过程中也需要用到一些带标记的样本。那么为什么不直接用监督学习方法呢？什么情况下用监督学习，什么情况下用异常检测呢？

实际，如果情况允许使用监督学习方法的话，监督学习可以获得一个性能更好的结果。但是监督学习要求我们有足够多的正类样本，以此来让我们获知正类样本大致是什么样子的。比如垃圾邮件处理。在这个例子中，我们有大量的垃圾邮件例子，可以获知垃圾邮件大致的特征。这种情况下就可以使用监督分类。

反过来，如果我们只有少量的正类和大量的反类。那么我们只有假设反类符合高斯分布，并通过异常检测识别正类样本。比如欺诈识别，我们就没有很多的欺诈样本，这种情况下我们就可以识别行为异常的账户存在欺诈的可能。

15.6 Choosing What Features to Use

在进行异常检测时如何来选择特征呢？

异常检测假设样本各特征独立并且符合高斯分布。那么对于各个特征，我们可以通过画图的方式确认其是否类似高斯分布。如果不是，我们可用过log或者指数函数的方式，将其转换为一个近似符合高斯分布的新特征。
此外可以对测试结果进行错误分析，找到错分样本中明显与其他样本区别的新特征（如值特别大或特别小的特征），以此来提高召回率。

15.7 Multivariate Gaussian Distribution (Optional)

异常检测的前提时假设各个特征间独立。那如果特征间存在相关性怎么办呢？

一个典型的例子，如果特性x1,x2正相关，那么样本点仅分布于x1大x2也大的地方或者x1小x2也小的地方。这时，对于一个x1不太小，x2不太大的点，用假设x1和x2独立的异常检测方式，则会认为p(x) = p(x1)*p(x2) 较大而误分。

那么对于这种情况怎么处理呢？

多元高斯分布闪亮登场了。我们不再对每个特征单独建模p(xi)，而是对向量x直接建模p(x)，并假设x符合多元高斯分布。通过估计其均值向量和协方差矩阵（ps. 协方差矩阵包含了各个特征的方差，以及各个特征的相关性等信息，信息量很大呀！），我们就可以获取p(x)。

15.8 Anomaly Detection using the Multivariate Gaussian Distribution

在进行异常检测的时候，高斯分布和多元高斯分布两种方法的关系是什么呢？

我们知道，是由于特征间存在相关性，高斯分布才不好用，不得不引入多元高斯分布。这是以牺牲运算效率为代价换取的（在计算协方差矩阵时，我们需要对大约n*n/2个参数进行估计，之所以除2是因为协方差矩阵是对称的，而高斯分布只需要对n个参数进行估计）。当然也不是没有好处，那就是可以自动的识别特征间的相关性。那什么时候高斯分布方式等与多元高斯方式呢？很简单啊，特征间不相关，协方差矩阵仅对角线非0不就行了。

采用高斯分布的方式可否处理特征间存在相关性的情况呢？

可以。只要引入xi/xj这样的新特征就可以了，但是这个过程是手动的。

什么时候采用多元高斯分布方式呢？

仅当m远大于n时，比如m>10n。这时候可以很好的估计协方差矩阵，否则可能遇到协方差矩阵估计出来都不可逆的情况。

真要是遇到了协方差不可逆怎么办？

首先这种情况概率很小。其次，如果真遇到了，先检查m是否>10n，再检查是否存在冗余特征。

高斯分布方式的优点是？

1. 快
2. 就算m小于n也搞的定

16. Recommender System

16.1 Problem Formulation

终于到了讲大名鼎鼎的推荐系统的时候了，这可能是当今互联网企业最受重视的机器学习应用了。
推荐系统自动预测用户对于某个商品的评分还进行推荐。

16.2 Content Based Recommendations

对于一个典型的推荐系统的例子–推荐电影，假如我们有关于电影内容的特征（如有多爱情片，有多动作片），那么这时候我们就可以使用基于内容的推荐。那它又是如何操作的呢？

其实思路很简单。对于每个用户，我们有一该用户对于某些影片的评分。我们以此为样本训练一个线性回归算法来预测用户对于没有看过的电影打几分。这样就可以判断是否可以把一部电影推荐给该用户。

在我看来，基于内容的推荐算法就像是一组线性回归的组合。

16.3 Collaborative Filtering

基于内容的推荐算法有个硬伤—需要获取电影的特征，这个消耗是很大的。那有没有什么其他办法呢？

协同过滤采用这样一种思路：
首先随即初始化theta，然后用theta来预测x，在反过来预测theta。周而复始，theta和x都会收敛到一个合理值。这样就避免了x的获取（这听起来像瞎忽悠）。

协同的意思是，每个用户评分几个电影，那么每个用户其实都协同在一起改进整个系（每个用户通过帮助系统更好的预测电影的特征值而改进了系统），进而预测每个用户对电影的评分。

16.4 Collaborative Filtering Algorithm

协同过滤到底是不是瞎忽悠呢？

当然不是。在协同过滤中，我们即学习了参数，又学习了特征。这似乎看起来有点鬼扯，其实为什么不能把参数和特征都看成是参数呢（此时特征变成了全1，模型从线性回归变成了一个非线性回归）。这样一说就顺理成章了。我们可以通过学习同时得到参数和特征（ps.这时就不要默认x0=1了，为啥？傻呀，所有的特征都是模型自动学习出来的，默认它干啥）。

16.5 Vectorization Low Rank Matrix Factorization

通过向量化表示协同过滤算法（也叫做 低秩矩阵分解），可以提高该算法计算的速度。

那我们又是如何向用户推荐电影的呢？

当学习到特征后（虽然某些特征我们并不知道它是什么，但是它确实是决定电影是否被高评分的重要因素），我们可以将与用户评分了电影相似的电影推荐给用户（这里的相似是指特征值之间的差距，即范数）。

16.6 Implementational Detail Mean Normalization

当我们进行协同过滤时，若碰到一个用户对所有电影都没有评分的情况如何处理呢？

如国不做预处理，我们会预测该用户对所有电影评分为0。这毫无意义，没有办法给他推荐电影啊。

这时候我们就可以作预处理–均值归一化。简单来说，就是对于特定电影，将已评分用户的评分均值，作为该用户对这部电影的评分预测值。

同样，对于一部电影从没有人评分过的情况，我们也可以利用类似的策略—预测为用户对所有电影的评分均值。不过这样意义不大。为什么呢？因为一部没有人评分过的电影，不值得推荐啊。

Programming Exercise 8:Anomaly Detection and Recommender System

本实践首先对异常检测算法进行了演示。在演示中，我们首先对一组二维数据进行高斯建模，估计它的mu和sigma。然后采用F1来选取最佳的epsilon，并通过图形化来演示异常检测的结果。在演示的最后，还将该方法推广到了一个100维的数据集。

在异常检测的实践过程中，并没有对原始数据进行均值归一化等操作。是否异常检测不需要做这些预处理呢？可能是的。均值归一化往往应用于梯度下降法之前，以提高收敛的速度。而在异常检测中，是否做均值归一化处理，并不会影响p的估计。所以异常检测并不必要。

本实践在第二部分还对推荐系统进行了演示。这里的推荐系统采用了协同过滤算法。在具体的实现中，还考虑了均值归一化等预处理。

17. Large Scale Machine Learning

17.1 Learning With Large Datasets

最近几年机器学习算法的突飞猛进，很大程度上归功于大数据的发展。但是这也带来了计算效率上的挑战（比如，在利用梯度下降法来优化J时，需要考虑所有样本的影响）。

在尝试使用大数据量来训练一个算法以期获取高性能前，我们应该先问下自己—如果我只是随即使用一个小的子集，是否也可以获得类似的性能？

为什么这么说呢？因为影响算法性能的因素大致有两条：

• 高方差 – 这个是可以通过更多样本训练来优化的
• 高偏差 – 这个无法通过更多样本训练来优化。甚至，随着样本数量的增多，偏差反而会增大。

所以，当我们识别这是一个高偏差算法（通过画学习曲线来识别），增加更多的训练样本，并不能显著提高算法的性能。此时，可能一个较小的子集就可以得到同样的性能。

或者，我们可以增加特征来解决高偏差问题，随后通过更多的训练样本来提高算法的性能。

17.2 Stochastic Gradient Descent

上一讲提到，大样本量给算法训练带来高性能的同时，也带来了计算效率上的挑战。典型的问题就是，如果使用梯度下降法，每次迭代我们都需要考虑每个样本的影响。如果样本量超大，每次样本数据读入内存都是个巨大的消耗，而这仅仅是一次迭代，为了一次移动。

为了解决这个问题，随机梯度下降法应运而生。其实思路很简单，梯度下降法每次移动是朝着最小值进行逼近，我们需要考虑所有的样本。随机梯度下降法为了减少计算量，仅向一个样本进行逼近。这样迭代中参数的移动路径将不是最短路径（看上去像是随机的，但是大趋势逼近于最小值附近的一个较小的范围），但是迭代速度快，整体的收敛速度快，这样就适合处理大量的数据。

依赖于总样本的量级，可能需要整体迭代1到10次。某些数量特别大的样本库（比如上亿），遍历一次样本库，就能得到不错的结果。

此外，为了更快的收敛，在应用随机梯度下降前，应该对样本库进行随机排序。

17.3 Mini-Batch Gradient Descent

梯度下降（也称批量梯度下降），每次迭代使用所有样本确认移动方向
随机梯度下降，每次用一个样本确认移动方向
迷你批量梯度下降，每次使用b个样本区人移动方向（b一般介于2到100间，常用10）。

什么时候迷你批量梯度下降能够以更快的速度收敛呢？那就是当你有一个并行处理的方案的时候。

17.4 Stochastic Gradient Descent Convergence

在应用随机梯度下降算法时，我们如何确定算法在收敛并确认在什么时刻应该结束学习呢?

对于批量梯度下降，我们画出J相对于迭代次数的曲线，并通过观察该曲线确认算法是否在收敛，并是否已经收敛完成。类似的，对于随机梯度下降，我们在每次迭代前，先计算cost值，并每1000次迭代（当然也可以采用其他次数，比如5000次。这样曲线会更加平坦，容易看出趋势，但是更大次数上的平均会产生更多的延迟，因为需要每5000次才计算一次趋势）计算一次平均值。通过该平均值相对于迭代次数的曲线，我们可以确认是否收敛，以及是否收敛完成。

17.5 Online learning

对于某些大型网站，它有持续的大量用户行为可以学习，这时就可以考虑使用在线学习算法。在线学习算法每次应用一个新的样本优化算法，用完就抛弃。因为对于大型网站，有大量源源不断的新用户行为，完全没必要进行存储。

此外，在线学习方法可以随着用户喜好慢慢的改变。

典型的应用例子包括，产品推荐，新闻内容推荐等等。

17.6 Map Reduce and Data Parallelism

处理大数据量的机器学习有个神器，那就是map reduce。它的思路很简单，即是将数据集拆分，交给各个电脑去计算，然后汇总。

应用map reduce的前提是你的计算可以拆分成大量的加法计算。而机器学习中最耗时的可能就是加法计算，比如计算J要用到所有的样本，计算梯度还是要用到所有的样本。

Map reduce不但可以应用于计算机集群，它还可以应用于单台计算机的多个cpu甚至cpu的多个核。但如果你用到了一些已经考虑到多核处理的线性计算库，并且算法进行了很好的向量化，那就完全不用考虑并行计算的问题。因为新型计算库已经为你搞定了这一切。

18. OCR

18.1 Problem Description and Pipeline

照片OCR是机器学习一个很重要的应用。要实现OCR，我们需要先找到一个个包括字符的矩形区域，将该矩形区域划分成一个个字符，最后再进行字符识别，有时我们还会对识别结果进行拼写检查。工程上，我们采用流水线的方式来实现每一个步骤，即实现几个模块，分别对应各个功能。

18.2 Sliding Windows

OCR可以描述为如下的流程：
图像—>文本矩形区—>字符分割—>字符识别

那么我们又是如何来找到矩形区域以及做字符分割的呢？

答案是滑窗。

对于文本矩形区，我们利用一个滑窗（大小可变），用监督学习算法来识别窗口中是否有文本（对于字符分割，识别是否有两个字符的分割）。存在文本的位置标记为1，没有的地方标记为0，这样我们就生成了一张黑白图。接下来我们用宽松因子（每个白点向右扩几个像素），将白色区域扩大。然后我们去掉比例不合理的区域，最后就剩下了目标矩形区域了。

18.3 Getting Lots of Data and Artificial Data

通过前面的学习我们知道，得数据者得天下。通过获得更多的数据，通常我们可以大幅提高机器学习算法的性能。

那如何获取大量的数据呢?

一种选择是通过人造数据。以OCR为例，我们可以

• 将一种字体（在网上我们可以成千种字体）的文字，附加到一系列随机背景中，生成新的样本
• 将字符作一列的变形来获取新的样本

再来看语音识别的例子，我们可以在要识别的语音中增加背景噪音生成新的样本。

但是有一点需要注意，随机的噪音没有什么鸟用。增加的误差应该在测试集中有代表性，说白了就是测试集中有的误差

此外我们也可以通过众包的方式廉价的获取大量的标注后的数据。

每当我们想提高我们模型的性能时，我们都应该问自己如下的问题：

1. 我们的模型是否是低偏差的（如果不是，考虑增加特征）
2. 我们要耗费多少时间来获取10倍于目前的数据量

可能你会得到一个让你surprise的答案。

18.4 Ceiling Analysis – What part of the pipeline to work on next

21世纪什么最值钱？— 时间

作为一个人工智能工程师，当你在开发一个人工智能系统时，如何决定下一步用你宝贵的时间来做什么，能够更好的提高你的产品的性能呢？

答案是 — 上限分析。

上限分析的思路很简单。如果你开发的产品采用了流水线系统，我们可以通过逐步将流水线中各个模块替换成真人，以此来确定通过提升特定模块来提高系统整体性能（如准确率）的空间。通过观察哪个模块提升的空间最大，来确定接下来我们把时间花在什么上面。

吴恩达讲了个真实故事，两个开发人员花了18个月的时间来提升系统中一个移除背景的模块的性能，还发了文章。结果最后发现18个月的努力对于整个系统系性能的提升只有0.1%。我擦，先做个上限分析有多么重要。

19. Summary

终于到总结了…

通过吴恩达老师的这门课程，我得以更好的了解机器学习。

在这门课中，我接触到

• 大量的监督学习算法，包括线性回归，逻辑回归，神经网络，支持向量机。
• 无监督学习算法，包括K-mean，PCA，异常检测
• 大量的应用和话题，像推荐系统，大规模机器学习系统（map reduce），CV中的滑窗
• 很多构建机器学习的实用建议。包括如何判断一个系统是否正常工作，偏差/方差均衡问题，正则化，如何决定下一步做什么
• 机器学习算法的评价方法。包括评价矩阵（查准率，召回率，F1分数），训练集/cv/test set
• 学习算法的调试。学习曲线，误差分析，上限分析

非常感谢吴恩达老师，制作了这么好的课程。同时也要感谢网络上热心网友的分享，让我能有机会接触到这么课程。最后也谢谢自己，能够攻克最初的困难坚持到现在。

人工智能的路上，继续前行，加油！！！