# 机器学习实战#(一)——KNN算法
一、KNN算法
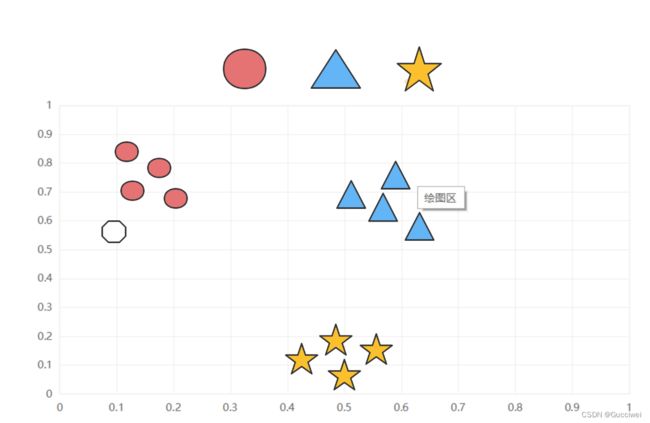
KNN算法也叫k-近邻算法,简单的说就是运用k算法采用测量不同特征值之间的距离的方法对日常生活中出现的人或物进行分类。它的算法核心思想就是:近朱者赤,近墨者黑。举个例子: 如图1.1所示假设坐标图中有3种颜色的图案,其中有一个白色的图案,要判断它应该属于哪种颜色,取决于它的坐标位置,经过计算它离红色图案的坐标位置更近,所以它最后属于红色类型。
图1.1
二、K算法的一般流程
(1)收集数据:线上或者线下收集。
(2)准备数据:可以使用结构化的数据格式,比如二维坐标。
(3)分析数据:可以使用任何方法。
(4)训练算法:不需要。
(5)测试算法:计算错误率。
(6)使用算法:首先需要输入样本数据和结构化的输出结果,然后运行k-近邻算法判定输入数据分别属于哪个分类,最后应用对计算出的分类执行后续的处理。
三、距离的计算
欧式距离:计算两点A、B之间的距离:
![]()
四、K值的确定
K近邻算法中的K是什么意思呢?
K近邻,是k个最近的邻居,也就是每个样本都可以用它最接近的k个邻居来代表。
K:临接近的数,在预测目标点时取几个临近的点来预测。
K值的确定:
(1)当K的取值过小时,会出现偏差,容易发生过拟合;
(2)当K的值取过大时,就相当于用较大邻域中的训练实例进行预测,学习的近似误差会增大。使预测发生错误,容易导致欠拟合。
(3) 所以K值的选取一般都比较小且基本都是奇数,同时也需要进行交叉验证。
五、具体实例分析
对人的BMI进行分析,也就是根据每个人的身高和体重对他的身材进行分类,判断他是否符合正常标准。比如偏瘦,正常,偏胖,很胖。
假设已知的数据集如下:
| 性别 | 身高(cm) | 体重(kg) | 指标 |
| 男 | 180 | 80 | 正常 |
| 男 | 175 | 55 | 偏瘦 |
| 男 | 170 | 98 | 偏胖 |
| 男 | 165 | 110 | 很胖 |
| 女 | 170 | 60 | 正常 |
| 女 | 165 | 50 | 偏瘦 |
| 女 | 160 | 75 | 偏胖 |
| 女 | 155 | 80 | 很胖 |
需要测试的数据集如下:
| 性别 | 身高(cm) | 体重(Kg) |
| 男 | 179 | 77 |
| 男 | 165 | 90 |
| 女 | 175 | 65 |
| 女 | 166 | 73 |
六、代码实现
导入数据集如下(其中1表示性别为男,2表示性别为女):
def createDataSet() :
# 八组特征
group = np.array([[1,180, 80], [1,175,55], [1,170, 98], [1,165, 110], [2,170, 60], [2,165,50], [2,155,80],[2, 160,75]])
# 八组特征的标签
labels = ['正常', '偏瘦', '偏胖', '很胖', '正常', '偏瘦', '偏胖','很胖']
return group, labels结果打印如下:
测试集数据如下(k值取3):
test1 = classify([1,179,77], group, labels, 3)
test2 = classify([1, 165, 90], group, labels, 3)
test3= classify([2, 175, 60], group, labels, 3)
test4= classify([2, 166, 73], group, labels, 3)
整体代码如下:
import operator
import numpy as np
from numpy import tile
def createDataSet() :
# 八组特征
group = np.array([[1,180, 80], [1,175,55], [1,170, 98], [1,165, 110], [2,170, 60], [2,165,50], [2,155,80],[2, 160,75]])
# 八组特征的标签
labels = ['正常', '偏瘦', '偏胖', '很胖', '正常', '偏瘦', '偏胖','很胖']
return group, labels
def classify(inX,dataSet,labels,k):
dataSetSize=dataSet.shape[0]
diffMat=tile(inX,(dataSetSize,1))-dataSet
sqDiffMat=diffMat**2
sqDistances=sqDiffMat.sum(axis=1)
distances=sqDistances**0.5
sortedDistIndices=distances.argsort()
classCount={}
for i in range(k):
voteIlabel=labels[sortedDistIndices[i]]
classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
if __name__ == '__main__':
# 创建数据集
group, labels = createDataSet()
print("group:\n", group, '\n', "labels:\n", labels)
test1 = classify([1,179,77], group, labels, 3)
print('该同学指标为:',test1)
test2 = classify([1, 165, 90], group, labels, 3)
print('该同学指标为:', test2)
test3= classify([2, 175, 60], group, labels, 3)
print('该同学指标为:', test3)
test4= classify([2, 166, 73], group, labels, 3)
print('该同学指标为:', test4)测试结果如下:
七、K-近邻算法的总结
(1)此次算法的实例还不够完整,还缺少数据分析
(2)k算法的是优点:简单易懂不需要训练过程; 缺点:样本不平衡的时候,对稀有类别的预测准确率低