pytorch 优化器

深度学习五个步骤：数据 ——> 模型 ——> 损失函数 ——> 优化器 ——> 迭代训练，通过前向传播，得到模型的输出和真实标签之间的差异，也就是损失函数，有了损失函数之后，模型反向传播得到参数的梯度，接下来就是优化器根据这个梯度去更新参数。

优化器

pytorch的优化器：更新模型参数。

在更新参数时一般使用梯度下降的方式去更新。梯度下降常见的基本概念

1. 导数：函数在指定坐标轴上的变化率；
2. 方向导数：指定方向上的变化率；
3. 梯度：一个向量，方向为方向导数取得最大值的方向。

所以梯度是一个向量，方向是导数取得最大值的方向，也就是增长最快的方向，而梯度下降是沿着梯度的负方向去变化。

优化器的属性和方法

class Optimizer:
    defaults: dict
    state: dict
    param_groups: List[dict]

    def __init__(self, params: _params_t, default: dict) -> None: ...
    def __setstate__(self, state: dict) -> None: ...
    def state_dict(self) -> dict: ...
    def load_state_dict(self, state_dict: dict) -> None: ...
    def zero_grad(self, set_to_none: Optional[bool]=...) -> None: ...
    def step(self, closure: Optional[Callable[[], float]]=...) -> Optional[float]: ...
    def add_param_group(self, param_group: dict) -> None: ...

• defaults:优化器的超参数，主要存储一些学习率、momentum的值等等
• state:用来存储参数的一些缓存。例如使用momentum的时候，需要用到前几次的梯度，就存在这。
• params_groups:管理参数组。是一个list。list的每一个元素是一个字典。字典中有一个'params'的key，其对应的值才是真正的参数
   

 optimizer的基本方法

zero_grad()

清空所管理参数的梯度。

参数是一个张量，张量有梯度grad.

pytorch有一个特性：张量梯度是不会清零的。在每一次反向传播采用autograd计算梯度的时候，是累加的。

所以应当在梯度求导之前（backward之前）把梯度清零。

step()

执行一步更新。

step()会采用梯度下降等策略，具体的策略有很多种，例如随机梯度下降法，momentum加动量的方法，自适应学习率的方法等。

add_param_group()

添加一组参数到优化器中。

优化器可以管理很多参数，这些参数是可以分组的。我们对不同组的参数可以有不同的超参数的设置。例如在模型的fintune中，对模型前面特征提取的部分希望他的学习率小一些，更新的慢一些；而后面的自己定义的全连接层，希望学习率更大一些。这样就可以把整个模型分成两组，一组是前面特征提取的参数，一组是后面全连接层的参数

state_dict()

获取优化器当前状态信息字典。

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
opt_state_dict = optimizer.state_dict()

print("state_dict before step:\n", opt_state_dict)

for i in range(10):
    optimizer.step()

print("state_dict after step:\n", optimizer.state_dict())
# 训练10次之后将模型的参数保存下来
torch.save(optimizer.state_dict(), os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

load_state_dict()

加载状态信息字典

optimizer = optim.SGD([weight], lr=0.1, momentum=0.9)
state_dict = torch.load(os.path.join(BASE_DIR, "optimizer_state_dict.pkl"))

print("state_dict before load state:\n", optimizer.state_dict())
optimizer.load_state_dict(state_dict)
print("state_dict after load state:\n", optimizer.state_dict())

学习率,动量的影响

在梯度下降的过程中，学习率起到控制参数更新的一个步伐的作用。

Momentum(动量、冲量)：结合当前的梯度与上一次更新的信息，用于当前更新。

import torch
import matplotlib.pyplot as plt



def func(x):
    return torch.pow(x, 3)

iteration = 100
m = 0.0
###设置学习率列表
lr_list = [0.01, 0.03,0.05,0.08]
###设置动量参数列表
momentum_list = [0.1,0.1,0.1,0.1]

loss_rec = [[] for l in range(len(lr_list))]


for i, lr in enumerate(lr_list):
    x = torch.tensor([2.], requires_grad=True)

    momentum = momentum_list[i]


    optimizer = torch.optim.SGD([x], lr=lr, momentum=momentum)

    for iter in range(iteration):

        y = func(x)
        y.backward()

        optimizer.step()
        optimizer.zero_grad()

        loss_rec[i].append(y.item())

for i, loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()

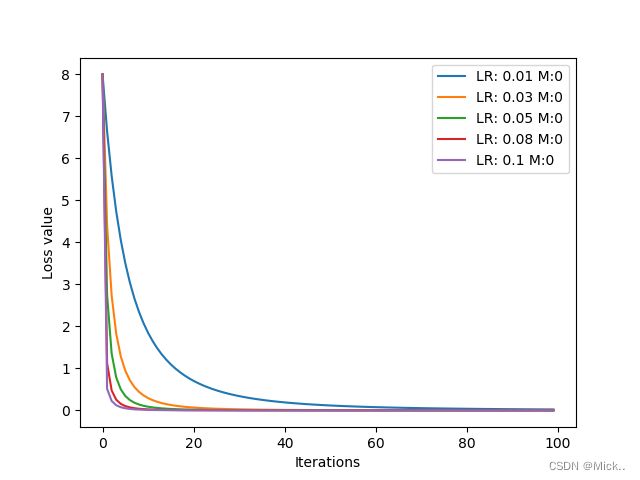
 学习率的影响，由下图可以看到，学习率越大，loss下降的就越快

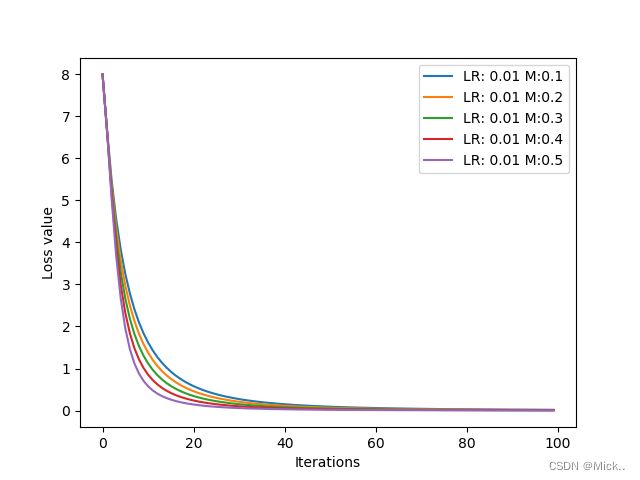
 动量的影响：

 

常见的优化器：

Adam优化器

torch.optim.Adam(params,
                lr=0.001,
                betas=(0.9, 0.999),
                eps=1e-08,
                weight_decay=0,
                amsgrad=False)

参考博客：

pytorch学习笔记十二：优化器_Dear_林的博客-CSDN博客_pytorch优化器