手写算法-python代码实现Kmeans++以及优化

聚类结果不稳定的优化方法

上篇文章，我们列举了Kmeans的不足之处，也用python代码实现了Kmeans聚类，但是跑出来的聚类结果不稳定，详情请看：
链接: 手写算法-python代码实现Kmeans
今天，我们来解决这个问题。

一次优化：kmeans++

问题点：随机选取k个数据，导致结果无法收敛。

因为随机选取，可能会使选取的几个数据点都非常靠近，不仅导致算法收敛很慢，还会导致结果只收敛到局部最小值。

解决思路：
使用Kmeans++的方法初始质心，流程如下：
1、从输入的数据点集合中随机选择一个点作为第一个聚类中心；
2、对于数据集中的每一个点xi，计算它与已选择的聚类中心中最近聚类中心的距离D(x)；
3、 选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大；
4、重复b和c直到选择出k个聚类质心；
5、利用这k个质心来作为初始化质心去运行标准的K-Means算法；

按照上面的流程，我们来修改Kmeans代码，实现Kmeans++。

import numpy as np
from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt


#无监督算法，学习过程就是训练质心的位置，进行聚类
class Kmeans:
    #添加init参数，默认init = 'random'就是标准Kmeans，init = 'Kmeans++'则为Kmeans++
    def __init__(self,k,init='random'):
        self.k = k
        self.init = init
    
    def calc_distance(self,x1,x2):
        diff = x1 - x2
        distances = np.sqrt(np.square(diff).sum(axis=1))
        return distances
    
    def fit(self,x):
        self.x = x
        m,n = self.x.shape
        
        if self.init == 'random':
            #随机选定k个数据作为初始质心，不重复选取
            self.original_ = np.random.choice(m,self.k,replace=False)
            #默认类别是从0到k-1
            self.original_center = x[self.original_]
        elif self.init == 'Kmeans++':
            first = np.random.choice(m)
            #储存在一个列表中
            index_select = [first]
            #继续选取k-1个点
            for i in range(1,self.k):
                all_distances = np.empty((m,0))
                for j in index_select:
                    #计算每个数据点到已选择的质心的距离
                    distances = self.calc_distance(self.x,x[j]).reshape(-1,1)
                    #把每个数据点到已选择的质心的距离储存在数组中，每个质心一列
                    all_distances = np.c_[all_distances,distances]
                #找到每个点到已选择质心的最小距离
                min_distances = all_distances.min(axis=1).reshape(-1,1)
                #在min_distances里面选取距离较大的点作为下一个质心，我们就选最大的点
                index = np.argmax(min_distances)
                index_select.append(index)
            #生成Kmeans++方法的初始质心，默认类别是从0到k-1
            self.original_center = x[index_select]

        while True:
            #初始化一个字典，以类别作为key，赋值一个空数组
            dict_y = {}
            for j in range(self.k):
                dict_y[j] = np.empty((0,n))
            for i in range(m):
                distances =self.calc_distance(x[i],self.original_center)
                #把第i个数据分配到距离最近的质心，存放在字典中
                label = np.argsort(distances)[0]
                dict_y[label] = np.r_[dict_y[label],x[i].reshape(1,-1)]
            centers = np.empty((0,n))
            #对每个类别的样本重新求质心
            for i in range(self.k):
                center = np.mean(dict_y[i],axis=0).reshape(1,-1)
                centers = np.r_[centers,center]
            #与上一次迭代的质心比较，如果没有发生变化，则停止迭代（也可考虑收敛时停止）
            result = np.all(centers == self.original_center)
            if result == True:
                break
            else:
                #继续更新质心
                self.original_center = centers

    def predict(self,x):
        y_preds = []
        m,n = x.shape
        for i in range(m):
            distances =self.calc_distance(x[i],self.original_center)
            y_pred = np.argsort(distances)[0]
            y_preds.append(y_pred)
        return y_preds

代码修改完毕，现在我们再次请出上篇文章用到的数据集，验证修改后，聚类结果稳不稳定：

#再次用到此数据集
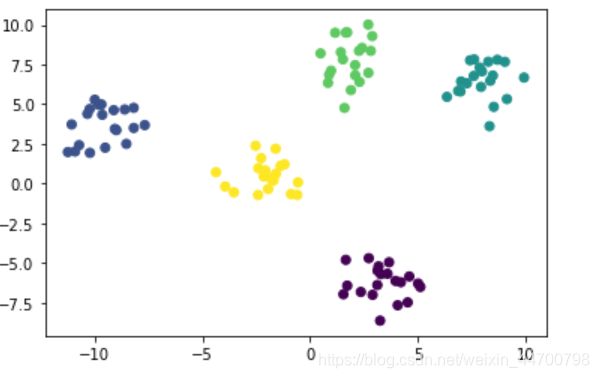
x,y = make_blobs(centers=5,random_state=20,cluster_std=1)
plt.scatter(x[:,0],x[:,1])
plt.show()

model = Kmeans(k=5,init = 'Kmeans++')
model.fit(x)
y_preds = model.predict(x)
plt.scatter(x[:,0],x[:,1],c=y_preds)
plt.show()

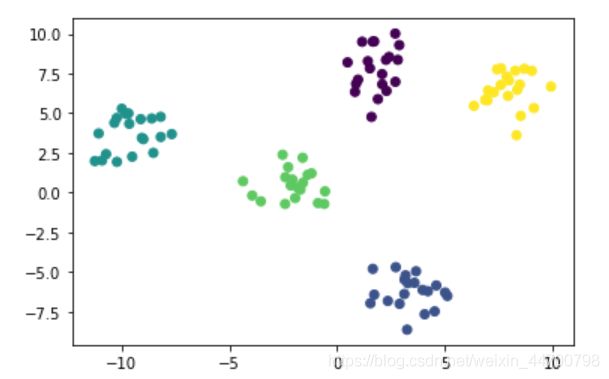
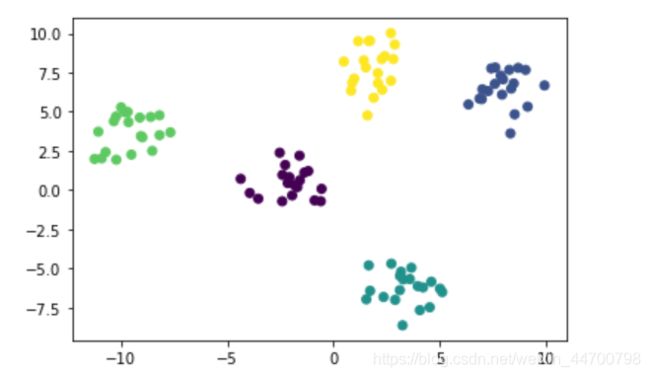
可以看到，不管执行多少遍，聚类结果都是稳定的，证明我们修改的Kmeans++成功！

二次优化：添加参数n_init

这是什么意思呢，意思很简单：
就是我执行n_init次，最终结果取最优的一次，最优怎么理解呢？
简单地说，就是所有样本点到所属的聚类质心的距离之和最小，即为最优。
$$J=min\sum _{i=1}^m||x_i-{\mu }_c{}^i|{|}^2$$

在Kmeans++方法选取质心的基础上，再添加参数n_init，双重保险，万无一失！哈哈。。。

找到n_init次运行中，J最小时，对应的聚类质心，即为最优解。
继续修改代码如下：

#无监督算法，学习过程就是训练质心的位置，进行聚类
class Kmeans:
    #添加init参数，默认init = 'random'就是标准Kmeans，init = 'Kmeans++'则为Kmeans++
    def __init__(self,k,n_init,init='random'):
        self.k = k
        self.n_init = n_init
        self.init = init
    
    def calc_distance(self,x1,x2):
        diff = x1 - x2
        distances = np.sqrt(np.square(diff).sum(axis=1))
        return distances
    
    def fit(self,x):
        m,n = x.shape
        if self.init == 'random':
            #随机选定k个数据作为初始质心，不重复选取
            self.original_ = np.random.choice(m,self.k,replace=False)
            #默认类别是从0到k-1
            self.original_center = x[self.original_]
        elif self.init == 'Kmeans++':
            first = np.random.choice(m)
            #储存在一个列表中
            index_select = [first]
            #继续选取k-1个点
            for i in range(1,self.k):
                all_distances = np.empty((m,0))
                for j in index_select:
                    #计算每个数据点到已选择的质心的距离
                    distances = self.calc_distance(x,x[j]).reshape(-1,1)
                    #把每个数据点到已选择的质心的距离储存在数组中，每个质心一列
                    all_distances = np.c_[all_distances,distances]
                #找到每个点到已选择质心的最小距离
                min_distances = all_distances.min(axis=1).reshape(-1,1)
                #在min_distances里面选取距离较大的点作为下一个质心，我们就选最大的点
                index = np.argmax(min_distances)
                index_select.append(index)
            #生成Kmeans++方法的初始质心，默认类别是从0到k-1
            self.original_center = x[index_select]

        while True:
            #初始化一个字典，以类别作为key，赋值一个空数组
            dict_y = {}
            for j in range(self.k):
                dict_y[j] = np.empty((0,n))
            for i in range(m):
                distances =self.calc_distance(x[i],self.original_center)
                #把第i个数据分配到距离最近的质心，存放在字典中
                label = np.argsort(distances)[0]
                dict_y[label] = np.r_[dict_y[label],x[i].reshape(1,-1)]
            centers = np.empty((0,n))
            #对每个类别的样本重新求质心
            for i in range(self.k):
                center = np.mean(dict_y[i],axis=0).reshape(1,-1)
                centers = np.r_[centers,center]
            #与上一次迭代的质心比较，如果没有发生变化，则停止迭代（也可考虑收敛时停止）
            result = np.all(centers == self.original_center)
            if result == True:
                return dict_y,centers
                break
            else:
                #继续更新质心
                self.original_center = centers
                
                
    def select_optimal(self,x):
        #储存每次的J值
        result = []
        #储存每次的聚类质心
        center = []
        for i in range(self.n_init):
            dict_y_i,center_i =self.fit(x)
            #计算J值
            for j in range(self.k):
                result_i = 0
                #计算第j个类别的样本到类别质心的距离之和
                distance_j = np.sum(self.calc_distance(dict_y_i[j],center_i[j]))
                result_i += distance_j
            result.append(result_i)
            center.append(center_i)
        #找到最小J值，对应的聚类质心
        index = np.argmin(result)
        self.original_center = center[index]  

    def predict(self,x):
        y_preds = []
        m,n = x.shape
        for i in range(m):
            distances =self.calc_distance(x[i],self.original_center)
            y_pred = np.argsort(distances)[0]
            y_preds.append(y_pred)
        return y_preds

二次修改过后，我们再次测试，结果应该是更加稳定了，看有没有bug

model = Kmeans(k=5,n_init=10,init = 'Kmeans++')
model.select_optimal(x)
y_preds = model.predict(x)
plt.scatter(x[:,0],x[:,1],c=y_preds)
plt.show()

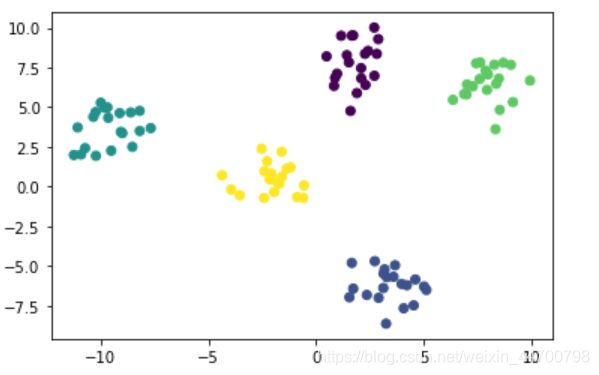
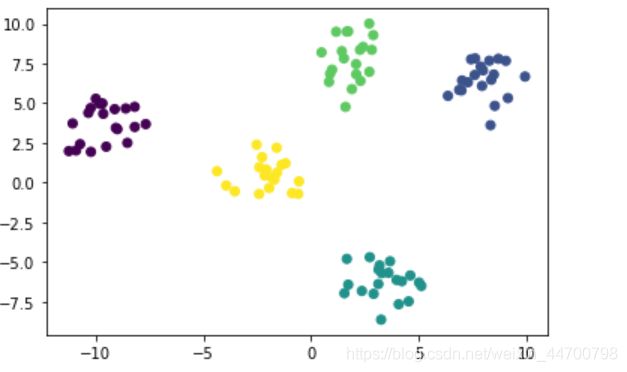
没有bug，结果也很稳定。
sklearn的效果上篇文章展示过，很稳定。

为什么sklearn的聚类结果这么稳定？
其实熟悉Kmeans的同学就应该清楚，我们这是复现了一部分sklearn里面KMeans的功能。

原因已经清楚了，sklearn里面的Kmeans，优化方法早就封装好了！

其他问题的优化方法

一、k值的选取问题。
方法1、肘部图法，一个样本集，k值越大，聚类的类别越多，
损失就越小，这里的损失就是我们上面说的J值，但是，当k值到达某个点
时，继续增大k值，损失的减小将变得缓慢，这个拐点对应的k值一般而
言，就是最佳k值。

方法2、从簇内的稠密程度和簇间的离散程度来评估聚类的效果。常见的
方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。
sklearn中已封装好，sklearn.metrics.calinski_harabasz_score
得分越高，聚类效果越好，得分最高时，就是最佳的k值。

1、肘部图法示例：

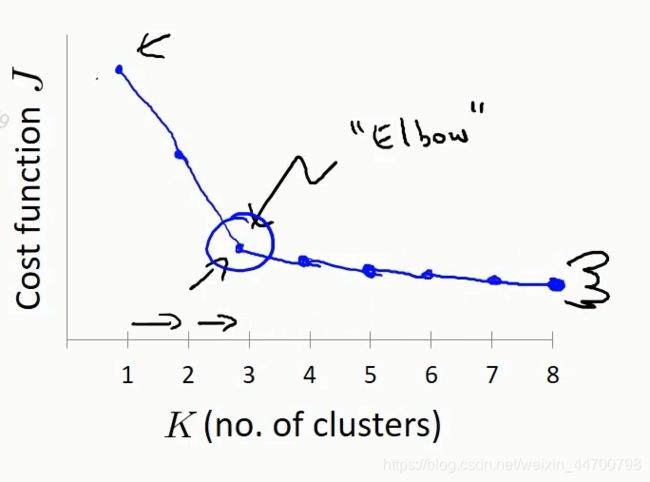
这个就迭代一下k值，然后画一下图像，比较简单，由于篇幅的原因，大家自行去实现一下，看看效果，这里就不写代码了；

2、metrics.calinski_harabasz_score对应的公式如下：
$$s(k)=\frac{tr(B_k)}{tr(W_k)}\frac{m-k}{k-1}$$
其中m为训练集样本数，k为类别数。Bk为类别之间的协方差矩阵，Wk为类别内部数据的协方差矩阵。tr为矩阵的迹。
score越大，代表类别内部数据的协方差越小，类别之间的协方差越大，也就是聚类效果越好。

用上面的数据集测试一下：

可以看到，K=5的时候，值最大，5就是我们要找的k值。

二、数据量很大时，时间复杂度很高，计算得很慢的问题
1、对距离计算的优化，elkan K-Means，利用了两边之和大于等于第三
边,以及两边之差小于第三边的三角形性质，来减少距离的计算。但是如
果样本的特征是稀疏的，有缺失值的话，这个方法就不使用了，此时某些
距离无法计算，则不能使用该算法。
Kmeans里面参数algorithm：有“auto”, “full” or “elkan”，“full”就是普通的欧氏距离，默认"auto"。

2、Mini Batch K-Means，Mini Batch，也就是用样本集中的一部分的样本
来做K-Means，不再使用全部样本，这样可以避免样本量太大时的计算难
题，算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也
会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。
sklearn里面直接封装有MiniBatchKMeans。

这样，Kmeans算法的问题，基本上都写了一下，至于Kmeans只适合处理凸样本集，不适合处理非凸样本集，这个问题，怎么解决，我们下一篇文章再写。