手写Kmeans

K-means聚类算法

1、聚类思想

所谓聚类算法是指将一堆没有标签的数据自动划分成几类的方法，属于无监督学习方法，这个方法要保证同一类的数据有相似的特征

2、导入所需的包

import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline

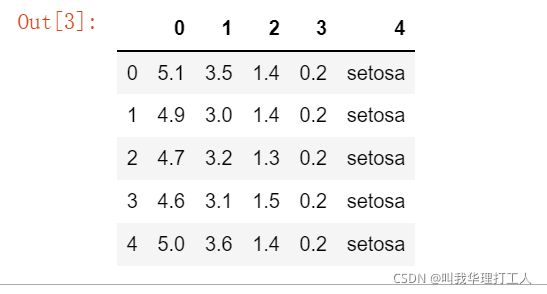
iris = pd.read_csv("iris.csv",header = None)
iris.head()

3、K-均值算法的python实现

根据K-均值算法的工作流程，我们写出伪代码：

创建k个点为初始质点（通常随机选择）
当任意一个点的簇分配结果发生改变时：
对数据集中的每个点：
对每个质心：
计算质心与数据点之间的距离
将数据点分配到距其最近的簇
对每个簇，计算簇中所有点的均值并将均值作为新的质心
直到簇不再发生改变或者达到最大迭代次数（自己设定）

伪代码中提到的“最近”在这里我们使用欧氏距离

3.1、构建一个计算距离的函数

统一量纲

如果数据中X整体都比较小，比如都是1到10之间的数，Y很大，比如都是1000以上的数，那么，在计算距离的时候Y起到的作用就比X大很多，X对于距离的影响几乎可以忽略，这也有问题。因此，如果K-Means聚类中选择欧几里德距离计算距离，数据集又出现了上面所述的情况，就一定要进行数据的标准化（normalization），即将数据按比例缩放，使之落入一个小的特定区间。(下面函数没有开平方以减少计算量）

def distEclud(arrA,arrB):
    d = arrA - arrB
    dist = np.sum(np.power(d,2),axis=1)
    return dist

3.2、编写自动生成随机质心的函数

在定义随机质心生成函数时，首先需要计算每列数值的范围，然后在该范围中随机生成指定个数的质心。
此处我们使用numpy.random.uniform()函数生成随机质心

"""
函数功能：随机生成k个质心
参数说明：
        dataSet：包含标签的数据集
        k:簇的个数
    返回：
        data_cent：k个质心
"""
def randCent(dataSet,k):
    n = dataSet.shape[1]
    data_min = dataSet.iloc[:,:n-1].min()
    data_max = dataSet.iloc[:,:n-1].max()
    data_cent = np.random.uniform(data_min,data_max,(k,n-1))
    return data_cent

函数用法（上面n-1不包含标签）

3.3、编写K-Means聚类函数

在执行k-means的时候，需要不断的迭代质心，因此我们需要两个可迭代容器来完成该目标：

第一个容器用于存放和更新质心，该容器可考虑使用list来执行，list不仅可迭代对象，同时list内不同元素索引位置也可
用于标记和区分各质心，即各簇的编号。

第二个容器泽需要记录、保存和更新各点到质心之间的距离，并能够方便对其进行比较，该容器可以使用一个三列的数组来
执行，其中第一列用于存放最近一次完成后某点到各质心的最短距离，第二列用于存放迭代后根据最短距离得到的代表对应
质心的数值索引，即所属簇，第三类用于存放上一次迭代后的所属簇，后两列用于比较所属簇是否发生变化，确定迭代结束。

def kMeans(dataSet,k,distMeas=distEclud,createCent=randCent):
    m,n = dataSet.shape
    centroids = createCent(dataSet,k)
    clusterAssment = np.zeros((m,3))
    clusterAssment[:,0] = np.inf
    clusterAssment[:,1:3] = -1
    result_set = pd.concat([dataSet,pd.DataFrame(clusterAssment)],axis = 1,ignore_index = True)
    clusterChanged = True
    time = 1
    while clusterChanged:
        clusterChanged = False
        for i in range(m):
            dist = distMeas(dataSet.iloc[i,:n-1].values,centroids)
            result_set.iloc[i,n] = dist.min()
            result_set.iloc[i,n+1] = np.where(dist == dist.min())[0]
        clusterChanged = not (result_set.iloc[:,-1] == result_set.iloc[:,-2]).all()
        if clusterChanged:
            cent_df = result_set.groupby(n+1).mean()
            centroids = cent_df.iloc[:,:n-1].values
            result_set.iloc[:,-1] = result_set.iloc[:,-2]
        time = time+1
        if(time==1000):
            break
    return centroids,result_set

4、有以下几点值得注意：

4.1、设置统一的操作对象result_set

为了调节和使用方便，此处将clusterAssment容易转换为了DataFrame并与输入原始数据集合并，组成的对象可作为后续调用的统一对象，该对象内既保留了原始数据也保存了迭代运算的中间结果，包括数据所属簇标记和数据质心距离等，该对象同时也作为最终函数返回结果；

4.2、判断质心是否发生改变条件

注意，在k-means中判断质心是否发生改变，即判断是否进行下一次迭代的依据并不是某点距离新的质心距离变短，而某点新的距离向量（到各质点的距离）中最短的分量位置是否发生改变，即质心变化后某点是否归属于另外的簇。在质心变化导致各点所属簇发生变化的过程中，点到质心的距离不一定会变短，即判断条件不能用下述语句表示

4.3、合并DataFrame后索引值为n列

这里有个小技巧，能够帮助迅速定位DataFrame合并后的索引，即两个DF合并后后者的第一列在合并后的DF索引值为n，第二列索引值为n+1

4.4、质心和类别一一对应

即在最后生成的结果中，centroids的行标即为result_set中各点所属类别

5、算法验证

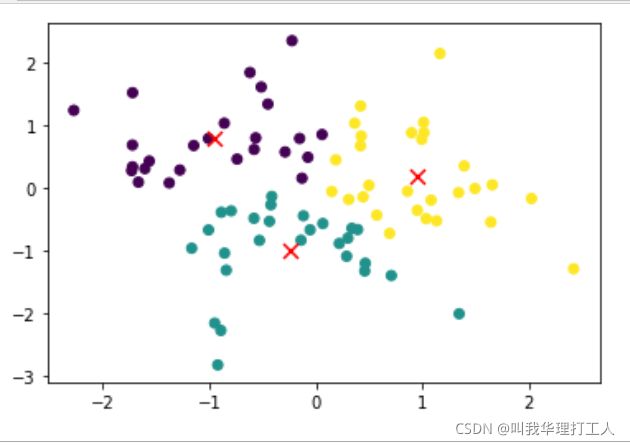
数编写完成后，先以testSet数据集测试模型运行效果（为了可以直观看出聚类效果，此处采用一个二维数据集进行验证）。testSet数据集是一个二维数据集，每个观测值都只有两个特征

6、把质心和散点数据集画到一起

plt.scatter(test_cluster.iloc[:,0],test_cluster.iloc[:,1],c=test_cluster.iloc[:,-1])
plt.scatter(test_cent[:,0],test_cent[:,1],color = "red",marker = "x",s=80);

7、误差平方和SSE计算

误差平方和（SSE）是聚类算法模型最重要的评估指标，根据n个观察值拟合适当的模型后，余下未能拟合部份(ei=yi一y平均)称为残差，其中y平均表示n个观察值的平均值，所有n个残差平方之和称误差平方和。以为各点所到质心的距离没有开方（即为平方）我们直接对所有列求和就好了

"""
函数功能：聚类学习曲线
参数说明：
    dataSet：原始数据集
    cluster：K-means聚类方法
    k:簇的个数
返回：误差平方和SSE
"""
def kcLearningCurve(dataSet, cluster = kMeans,k = 10):
    n = dataSet.shape[1]
    SSE = []
    for i in range(1,k):
        centroids,result_set = cluster(dataSet,i+1)
        SSE.append(result_set.iloc[:,n].sum())
    plt.plot(range(2,k+1),SSE,"--o")
    return SSE

kcLearningCurve(iris)

8、K-Means的优缺点

8.1、优点：

1、原理比较简单，实现也是很容易，收敛速度快。

2、当结果簇是密集的，而簇与簇之间区别明显时, 它的效果较好。

3、主要需要调参的参数仅仅是簇数k。

8.2、缺点：

1、K值需要预先给定，很多情况下K值的估计是非常困难的。

2、K-Means算法对初始选取的质心点是敏感的，不同的随机种子点得到的聚类结果完全不同 ，对结果影响很大。

3、对噪音和离群点比较的敏感。

4、采用迭代方法，可能只能得到局部的最优解，而无法得到全局的最优解。

5、无法发现任意簇,因为K-Means算法主要采用欧式距离函数度量数据对象之间的相似度,并且采用误差平方和作为准则函数,通常只能发现数据对象分布较均匀的球状簇.

8.3、改进方法：

针对 1 ：1、中存在的问题主要是 K 的值必须认为预先设定，并且在整个算法执行过程中无法更改。此时，可以利用 ISODATA 算法：当属于某个类别的样本数过少，就将这个类别剔除；当属于这个类别的样本过多、分散程度很大的时候，就将这个类别分为两个子类，此时 K 也就会 + 1了

针对 2 ：K-means ++ 不再随机选择 K 个聚类中心：假设已经选取了 m 个聚类中心（ 0 < m < K）,m = 1时，随机选择一个聚类中心点；在选取第 m+1 个点的时候，距离当前 m 个聚类中心点的中心越远的点，越会以更高的概率被选为第 m+1 个聚类中心。这种方法在一定程度上可以让“随机”选择的聚类中心点的分布更均匀。此外还有 canopy 算法等。

针对 3 ：针对离群点和噪声点，我们可以使用一些算法，比如 RANSAC 、LOF 等剔除离群点。此外，基于 K-means 的改进算法有 k-medoids 和 k-medians

针对 4 ：对于只能得到局部最优解，我们可以采用二分K-means，将所有点作为一个簇，然后将该簇一分为二，选择下一个簇继续进行划分。选择哪一个簇进行划分取决于：该簇的SSE（误差平方和）的值最大。而划分的方法还是K-means的方法，只是簇的个数k=2。通过不断重复直，到达到需要的簇数量。

针对 5 ：K-means 是使用欧式距离来测量，显然，这种度量方式并不适合于所有的数据集。换句话说，K-means 比较适合聚那些球状的簇。参照 SVM 中核函数的思想，将样本映射到另外一个特征空间，就可以改善聚类效果。代表算法是;kernel K-means。

改进算法一：K-means++

import math
import random
from sklearn import datasets

def euler_distance(point1, point2):
    """
    计算两点之间的欧式距离，支持多维
    """
    distance = 0.0
    for a, b in zip(point1, point2):
        distance += math.pow(a - b, 2)
    return math.sqrt(distance)
#计算最小距离
def get_closest_dist(point, centroids):
    min_dist = math.inf  # 初始设为无穷大
    for i, centroid in enumerate(centroids):
        dist = euler_distance(centroid, point)
        if dist < min_dist:
            min_dist = dist
    return min_dist

def kpp_centers(data_set, k):
    """
    从数据集中返回 k 个对象可作为质心
    """
    cluster_centers = []
    cluster_centers.append(random.choice(data_set))
    d = [0 for _ in range(len(data_set))]
    for _ in range(1, k):
        total = 0.0
        for i, point in enumerate(data_set):
            d[i] = get_closest_dist(point, cluster_centers) # 与最近一个聚类中心的距离
            total += d[i]
        total *= random.random()
        for i, di in enumerate(d): # 轮盘法选出下一个聚类中心；
            total -= di
            if total > 0:
                continue
            cluster_centers.append(data_set[i])
            break
    return cluster_centers

iris = datasets.load_iris()
cent = kpp_centers(iris.data, 3)
cent

改进算法二：isodata算法

图像展示

从图中可以看出，在第八次迭代之后，聚类就已经收敛了，从第八次到第十次迭代，聚类的状态就已经不再发生变化啦。
这个数据最好的分类中心是三个，即使初始设置的类别中心为5类，但是经过ISODATA聚类之后，还是能得到客观上所看到的三个类别中心。而如果是K-Means分类法，如果我们设置初始类别中心为5的话，最后得到的一定也是5类，和客观类别中心不符合。

算法优点

可以在聚类过程中自动调整类别个数和类别中心，使聚类结果能更加靠近客观真实的聚类结果。

算法缺点

需要设置的参数比较多，参数值不好确定。不同的参数之间相互影响，而且参数的值和聚类的样本集合也有关系，要得到好的聚类结果，需要有好的初始设置值，可以通过多次设置不同的值进行不同的实验，然后取一些已知的样本来检验聚类结果的精度，以最后取得更好的分类结果的那次实验为准；或者考虑和其他方法相结合来得到更好的分类结果。

二分K-means

1、所有点作为一个簇
2、将其一分为二
3、将误差平方和大的簇划分为两个簇
4、以此进行下去，直到达到用户所需的簇的个数