一种无人机配合卡车配送的车辆路径规划模型
文章目录
- TSP 模型
-
- 模型参数
- 决策变量
- 约束条件
- 目标函数
- 可视化示例
- VRP 模型
-
- 模型参数
- 决策变量
- 约束条件
- 目标函数
- 可视化示例
- 参考文献
- 代码分享
TSP 模型
模型参数
| 参数 | 含义 |
|---|---|
| N N N | 所有点的集合(含起止点) |
| M M M | 可以使用无人机配送的点的集合 |
| O O O | 起止点 |
| d i , j d_{i, j} di,j | 点 i i i 到点 j j j 的距离 |
| c c c | 无人机配送的距离成本系数 |
决策变量
| 变量 | 类型 | 含义 |
|---|---|---|
| x i , j x_{i, j} xi,j | 0-1 | 卡车是否经过从点 i i i 到点 j j j 的路径 |
| y i , j y_{i, j} yi,j | 0-1 | 无人机是否经过从点 i i i 到点 j j j 的路径 |
| s i s_{i} si | 0-1 | 点 i i i 是否由卡车配送 |
| a i , j a_{i, j} ai,j | R + 0 R^{0}_{+} R+0 | 用于消除子回路,从点 i i i 到点 j j j 的路径(弧)的前序弧数 |
约束条件
(1) 流入/流出
(1a) 只能使用卡车配送的点
∑ j ∈ N x j , i = 1 ∀ i ∈ N \ M ∑ j ∈ N x i , j = 1 ∀ i ∈ N \ M \sum_{j \in N} x_{j, i} = 1 \quad \forall i \in N \backslash M \\ \sum_{j \in N} x_{i, j} = 1 \quad \forall i \in N \backslash M j∈N∑xj,i=1∀i∈N\Mj∈N∑xi,j=1∀i∈N\M
(1b) 可以使用无人机配送的点
∑ j ∈ N x j , i + y j , i = 1 ∀ i ∈ M ∑ j ∈ N x i , j + y i , j = 1 ∀ i ∈ M ∑ j ∈ N y j , i = ∑ j ∈ N y i , j ∀ i ∈ M \sum_{j \in N} x_{j, i} + y_{j, i} = 1 \quad \forall i \in M \\ \sum_{j \in N} x_{i, j} + y_{i, j} = 1 \quad \forall i \in M \\ \sum_{j \in N} y_{j, i} = \sum_{j \in N} y_{i, j} \quad \forall i \in M j∈N∑xj,i+yj,i=1∀i∈Mj∈N∑xi,j+yi,j=1∀i∈Mj∈N∑yj,i=j∈N∑yi,j∀i∈M
(2) 去除自循环
∑ i ∈ N x i , i = 1 ∑ i ∈ N y i , i = 1 \sum_{i \in N} x_{i, i} = 1 \\ \sum_{i \in N} y_{i, i} = 1 i∈N∑xi,i=1i∈N∑yi,i=1
(3) 是否由卡车配送
s i = ∑ j ∈ N x i , j ∀ i ∈ N \ O s_{i} = \sum_{j \in N} x_{i, j} \quad \forall i \in N \backslash O si=j∈N∑xi,j∀i∈N\O
(4) 子回路去除
∑ j ∈ N \ { i } a i , j − ∑ j ∈ N \ { O , i } a j , i = s i ∀ i ∈ N \ O a i , j ≤ ∣ N ∣ ⋅ x i , j ∀ i ∈ N \ O ∀ j ∈ N \sum_{j \in N \backslash \{ i \}} a_{i, j} - \sum_{j \in N \backslash \{ O, i \}} a_{j, i} = s_{i} \quad \forall i \in N \backslash O \\ a_{i, j} \leq |N| \cdot x_{i, j} \quad \forall i \in N \backslash O \quad \forall j \in N j∈N\{i}∑ai,j−j∈N\{O,i}∑aj,i=si∀i∈N\Oai,j≤∣N∣⋅xi,j∀i∈N\O∀j∈N
(5) 无人机配送的流入点和流出点,符合卡车路径的先后关系
y i , j + y j , k ≤ 2 ⋅ x i , k + 1 ∀ j ∈ M ∀ i ∈ N ∀ k ∈ N y_{i, j} + y_{j, k} \leq 2 \cdot x_{i, k} + 1 \quad \forall j \in M \quad \forall i \in N \quad \forall k \in N yi,j+yj,k≤2⋅xi,k+1∀j∈M∀i∈N∀k∈N
(6) 只有一架无人机
∑ j ∈ N y i , j ≤ 1 ∀ i ∈ N ∑ j ∈ N y j , i ≤ 1 ∀ i ∈ N \sum_{j \in N} y_{i, j} \leq 1 \quad \forall i \in N \\ \sum_{j \in N} y_{j, i} \leq 1 \quad \forall i \in N j∈N∑yi,j≤1∀i∈Nj∈N∑yj,i≤1∀i∈N
目标函数
最小化,加权距离成本
m i n ∑ i ∈ N ∑ j ∈ N x i , j ⋅ d i , j + y i , j ⋅ d i , j ⋅ c min \quad \sum_{i \in N} \sum_{j \in N} x_{i, j} \cdot d_{i, j} + y_{i, j} \cdot d_{i, j} \cdot c mini∈N∑j∈N∑xi,j⋅di,j+yi,j⋅di,j⋅c
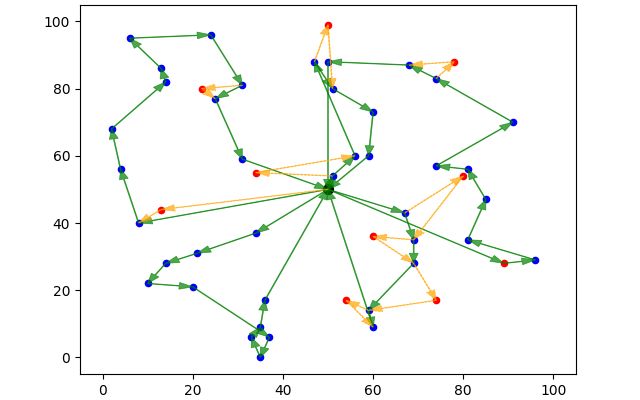
可视化示例
VRP 模型
模型参数
| 参数 | 含义 |
|---|---|
| N N N | 所有点的集合(含起止点) |
| M M M | 可以使用无人机配送的点的集合 |
| O O O | 起止点 |
| w i w_{i} wi | 点 i i i 的配送重量 |
| W W W | 卡车的载重上限 |
| d i , j d_{i, j} di,j | 点 i i i 到点 j j j 的距离 |
| c c c | 无人机配送的距离成本系数 |
| B B B | 一个充分大的数 |
决策变量
| 变量 | 类型 | 含义 |
|---|---|---|
| x i , j x_{i, j} xi,j | 0-1 | 卡车是否经过从点 i i i 到点 j j j 的路径 |
| y i , j y_{i, j} yi,j | 0-1 | 无人机是否经过从点 i i i 到点 j j j 的路径 |
| s i s_{i} si | 0-1 | 点 i i i 是否由卡车配送 |
| z i , j z_{i, j} zi,j | R + 0 R^{0}_{+} R+0 | 从点 i i i 到点 j j j 的路径上的卡车载重,可用于消除子回路 |
约束条件
(1) 流入/流出
(1a) 只能使用卡车配送的点
∑ j ∈ N x j , i = 1 ∀ i ∈ N \ { O } \ M ∑ j ∈ N x i , j = 1 ∀ i ∈ N \ { O } \ M \sum_{j \in N} x_{j, i} = 1 \quad \forall i \in N \backslash \{O\} \backslash M \\ \sum_{j \in N} x_{i, j} = 1 \quad \forall i \in N \backslash \{O\} \backslash M j∈N∑xj,i=1∀i∈N\{O}\Mj∈N∑xi,j=1∀i∈N\{O}\M
(1b) 可以使用无人机配送的点
∑ j ∈ N x j , i + y j , i = 1 ∀ i ∈ M ∑ j ∈ N x i , j + y i , j = 1 ∀ i ∈ M ∑ j ∈ N y j , i = ∑ j ∈ N y i , j ∀ i ∈ M \sum_{j \in N} x_{j, i} + y_{j, i} = 1 \quad \forall i \in M \\ \sum_{j \in N} x_{i, j} + y_{i, j} = 1 \quad \forall i \in M \\ \sum_{j \in N} y_{j, i} = \sum_{j \in N} y_{i, j} \quad \forall i \in M j∈N∑xj,i+yj,i=1∀i∈Mj∈N∑xi,j+yi,j=1∀i∈Mj∈N∑yj,i=j∈N∑yi,j∀i∈M
(2) 去除自循环
∑ i ∈ N x i , i = 1 ∑ i ∈ N y i , i = 1 \sum_{i \in N} x_{i, i} = 1 \\ \sum_{i \in N} y_{i, i} = 1 i∈N∑xi,i=1i∈N∑yi,i=1
(3) 是否由卡车配送
s i = ∑ j ∈ N x i , j ∀ i ∈ N \ O s_{i} = \sum_{j \in N} x_{i, j} \quad \forall i \in N \backslash O si=j∈N∑xi,j∀i∈N\O
(4) 载重限制,并消除子回路
z i , j ≥ w j + ∑ k ∈ N \ { j } z j , k + ∑ u ∈ M \ { u } y j , u ⋅ w u + ( x i , j − 1 ) ⋅ B ∀ j ∈ N \ { O } ∀ i ∈ N z i , j ≤ x i , j ⋅ B ∀ j ∈ N \ { O } ∀ i ∈ N x i , j + x j , i ≤ 1 ∀ j ∈ N \ { O } ∀ i ∈ N \ { O } z_{i, j} \geq w_{j} + \sum_{k \in N \backslash \{j\}} z_{j, k} + \sum_{u \in M \backslash \{u\}} y_{j, u} \cdot w_{u} + (x_{i, j} - 1) \cdot B \quad \forall j \in N \backslash \{O\} \quad \forall i \in N \\ z_{i, j} \leq x_{i, j} \cdot B \quad \forall j \in N \backslash \{O\} \quad \forall i \in N \\ x_{i, j} + x_{j, i} \leq 1 \quad \forall j \in N \backslash \{O\} \quad \forall i \in N \backslash \{O\} zi,j≥wj+k∈N\{j}∑zj,k+u∈M\{u}∑yj,u⋅wu+(xi,j−1)⋅B∀j∈N\{O}∀i∈Nzi,j≤xi,j⋅B∀j∈N\{O}∀i∈Nxi,j+xj,i≤1∀j∈N\{O}∀i∈N\{O}
(5) 无人机配送的流入点和流出点,符合卡车路径的先后关系
y i , j + y j , k ≤ 2 ⋅ x i , k + 1 ∀ j ∈ M ∀ i ∈ N ∀ k ∈ N y_{i, j} + y_{j, k} \leq 2 \cdot x_{i, k} + 1 \quad \forall j \in M \quad \forall i \in N \quad \forall k \in N yi,j+yj,k≤2⋅xi,k+1∀j∈M∀i∈N∀k∈N
(6) 只有一架无人机
∑ j ∈ N y i , j ≤ 1 ∀ i ∈ N ∑ j ∈ N y j , i ≤ 1 ∀ i ∈ N \sum_{j \in N} y_{i, j} \leq 1 \quad \forall i \in N \\ \sum_{j \in N} y_{j, i} \leq 1 \quad \forall i \in N j∈N∑yi,j≤1∀i∈Nj∈N∑yj,i≤1∀i∈N
目标函数
一级目标:最小化,总卡车数;
二级目标:最小化,加权距离成本
m i n ∑ j ∈ N \ { O } x 0 , j ⋅ B + ∑ i ∈ N ∑ j ∈ N ( x i , j ⋅ d i , j + y i , j ⋅ d i , j ⋅ c ) min \quad \sum_{j \in N \backslash \{O\}} x_{0, j} \cdot B + \sum_{i \in N} \sum_{j \in N} (x_{i, j} \cdot d_{i, j} + y_{i, j} \cdot d_{i, j} \cdot c) minj∈N\{O}∑x0,j⋅B+i∈N∑j∈N∑(xi,j⋅di,j+yi,j⋅di,j⋅c)
可视化示例
参考文献
2015, The flying sidekick traveling salesman problem Optimization of drone-assisted parcel delivery
代码分享
https://blog.csdn.net/Zhang_0702_China/article/details/119391030