《图算法》第六章 社区检测算法-3
对图算法有兴趣的朋友可以关注微信公众号 ：《 Medical与AI的故事》
原文链接：《图算法》第六章-3 社区检测算法
Louvain模块化算法
Louvain模块化算法在将节点分配给不同的组时，通过比较社区密度来查找集群。您可以将其视为一种“假设”分析，尝试各种分组，以达到全球最佳。
Louvain算法于2008年提出，是最快的模块化算法之一。除了检测社区之外，它还揭示了不同规模的社区层次。这对于理解不同粒度级别的网络结构很有用。
与平均或随机样本相比，Louvain通过查看聚类中连接的密度来量化节点分配给一个组的最佳程度。这种分配社区的测量称为模块化。
基于品质分组的模块化
模块化是一种通过将一个图划分为更粗粒度的模块（或聚类），然后测量分组强度来发现社区的技术。与仅仅观察一聚类内连接的浓度不同，该方法将给定聚类中的关系密度与聚类间的密度进行比较。这些分组的品质的度量方法称为模块化。
模块化算法先构成局部社区之后在全局范围内优化，使用多个迭代测试不同的分组并增加粒度。该策略确定了社区层次结构，并提供了对整体结构的广泛理解。然而，所有模块化算法都有两个缺点：
- 他们会将较小的社区合并为较大的社区。
- 当存在具有类似模块性的多个候选分区时，可能会出现平台，形成局部最大值并阻止进展。
有关更多信息，请参阅B.H.Good、Y.A.De Montjoye和A.Clauset的论文“The Performance of Modularity Maximization in Practical Contexts”。
计算模块化
简化的模块化计算是基于给定组中关系的比率（fraction）减去期望比率（如果关系在所有节点之间随机分布）。该值始终介于1和-1之间，正值表示的关系密度比您预期的几率更大，负值则相反。图6-11说明了基于节点分组的几个不同模块化得分。
图6-11 基于不同分区选择的四个模块化得分
分组的模块化公式为：
在这个公式中
- L是整个组(group)中的关系数。
- Lc是一个分区（partition）中的关系数。
- Kc是一个分区中节点的总度数。
图6-11的顶部的最佳分区（Optimal Partition）计算如下：
暗分区是7/13-(15/(213))^2 = 0.205
亮分区是5/13-(11/(213))^2 = 0.206
加在一起M = 0.205 + 0206 = 0.41
最初，Louvani模块化算法在所有节点上局部优化模块化，找到小的社区；然后将每个小社区被合并到一个较大的联合节点，并重复第一步，直到达到全局最优。
该算法包括两个步骤的重复应用，如图6-12所示。
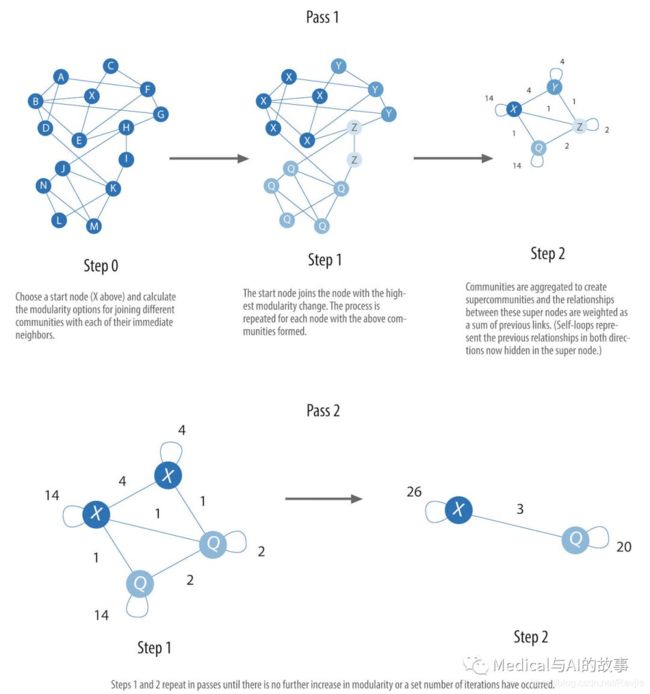
图6-12。Louvain算法过程
Louvain算法的步骤包括：
- 将节点“贪婪”地分配给社区，有利于模块化的局部优化。
- 基于第一步中发现的社区定义更粗粒度的网络。这种粗粒度的网络将在算法的下一次迭代中使用。
重复这两个步骤，直到无法进一步模块化，也就是无法进一步进行增加社区的重新分配为止。
Louvain模块化是模块化的优化算法。第一步的优化步骤是评估组的模块性Louvain使用以下公式来实现这一点：
在这个公式里
- U和V是节点。
- m是整个图的总关系权重（在模块化公式中2m是常见的归一化的值）。
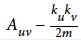是u和v之间关系的强度和网络中随机分配的结果的相比的结果
- Auv是u和v之间的关系权重
- Ku是u的所有关系权重的总和
- Kv是v的所有关系权重的总和
- δ (cu, cv) ：当u和v被分配到同一社区时为1，当它们处于不同社区时为0。
第一步的另一部分评估了如果将一个节点移动到另一个组中，模块性的变化。Louvain使用了这个公式更复杂的变体，最后确定了最佳的组分配。
Louvain模块化的使用场景
使用Louvain模块化在庞大的网络中查找社区。该算法采用启发式算法，而不是昂贵而精确的模块化算法。因此，当标准的模块化算法在这些图上可能会遇到困难的时候，Louvain可以被派上用场。
Louvain对于评估复杂网络的结构也非常有帮助，尤其是发现许多层次结构——就像你可能在犯罪组织中发现的层级结构一样。该算法可以提供结果，您可以在其中放大不同级别的粒度，并在子社区中查找子社区中的子社区。
示例用例包括：
- 检测网络攻击。Louvain算法被S. V. Shanbhaq用于2016年的一项研究，该研究是关于大规模网络安全网络中快速社区检测的应用。一旦这些社区被发现，它们就可以用来检测网络攻击。
- 从Twitter和YouTube等在线社交平台中提取主题，基于文档中共同出现的术语，作为主题建模过程的一部分。这一方法在G. S. Kido、R. A. Igawa和S. Barbon Jr.，“Topic Modeling Based on Louvain Method in Online Social Networks”一文中进行了描述。
- 如D. Meunier等人的“Hierarchical Modularity in Human Brain Functional Networks”所述，在大脑功能网络中找到层次化的社区结构。
模块化优化算法（包括Louvain）面临两个问题。首先，这些算法可以忽略大型网络中的小型社区。您可以通过评估中间合并步骤来克服这个问题。其次，在具有重叠社区的大型图中，模块化优化器可能无法正确地确定全局最大值。在后一种情况下，我们建议使用任意的模块化算法作为粗略估计的指导，但不完全准确。
在Neo4j上使用Louvain模块化
让我们看一下Louvain模块化如何应用。我们可以在图中执行如下的查询。
CALL algo.louvain.stream("Library", "DEPENDS_ON")
YIELD nodeId, communities
RETURN algo.getNodeById(nodeId).id AS libraries, communities
查询中传入的参数如下：
如下是运行的结果(译者：Neo4j Louvain在algo3.5.4.0上运行并不成功)
+------------------+--------------+
| libraries | communities |
+------------------+--------------+
| pytz | [0, 0] |
| pyspark | [1, 1] |
| matplotlib | [2, 0] |
| spacy | [2, 0] |
| py4j | [1, 1] |
| jupyter | [3, 2] |
| jpy-console | [3, 2] |
| nbconvert | [4, 2] |
| ipykernel | [3, 2] |
| jpy-client | [4, 2] |
| jpy-core | [4, 2] |
| six | [2, 0] |
| pandas | [0, 0] |
| numpy | [2, 0] |
| python-dateutil | [2, 0] |
+------------------+--------------+
“社区”列描述节点分为两个级别的社区。数组中的最后一个值是最终社区，另一个是中间社区。
分配给中间社区和最终社区的数字只是标签，没有可测量的意义。将它们视为指示哪些社区节点属于的标签，例如“属于标记为0的社区”、“标记为4的社区”等等。
例如，matplotlib的结果是[2,0]。这意味着Matplotlib的最终社区标记为0，中间社区标记为2。
如果我们使用该算法的写入版本存储这些社区，然后再对其进行查询，那么更容易看到这是如何工作的。以下查询将运行Louvain算法，并将结果存储在每个节点的communities属性中：
CALL algo.louvain("Library", "DEPENDS_ON")
我们还可以使用该算法的流版本存储结果社区，然后调用set子句来存储结果。下面的查询显示了我们如何执行此操作：
CALL algo.louvain.stream("Library", "DEPENDS_ON")
YIELD nodeId, communities
WITH algo.getNodeById(nodeId) AS node, communities
SET node.communities = communities
一旦我们运行以上任何的查询，我们可以用如下的查询来找到最终的聚类:
MATCH (l:Library)
RETURN l.communities[-1] AS community, collect(l.id) AS libraries
ORDER BY size(libraries) DESC
l.communities[-1] 从存储的数组中返回最后一个元素。
运行查询会得到如下的输出：
+------------+--------------------------------------------------------------------+
| community | libraries |
+------------+--------------------------------------------------------------------+
| 0 | [pytz, matplotlib, spacy, six, pandas, numpy, python-dateutil] |
| 2 | [jupyter, jpy-console, nbconvert, ipykernel, jpy-client, jpy-core] |
| 1 | [pyspark, py4j] |
+------------+--------------------------------------------------------------------+
这个聚类和我们在连接组件算法中看到的一样。matplotlib与pytz、spacy、six、panda、numpy和pythondateutil在一个社区中。我们可以在图6-13中更清楚地看到这一点。
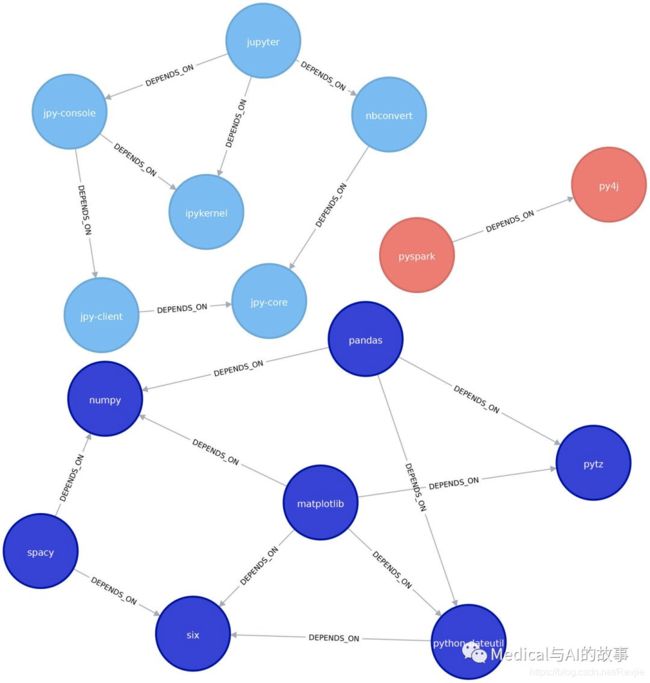
图6-13。Louvain算法发现的簇
Louvain算法的另一个特点是我们也可以看到中间聚类。这将向我们展示比最终层更细粒度的集群：
MATCH (l:Library)
RETURN l.communities[0] AS community, collect(l.id) AS libraries
ORDER BY size(libraries) DESC
运行该查询可以得到如下的结果：
+----------+--------------------------------------------+
| community| libraries |
+----------+--------------------------------------------+
| 2 | [matplotlib, spacy, six, python-dateutil] |
| 4 | [nbconvert, jpy-client, jpy-core] |
| 3 | [jupyter, jpy-console, ipykernel] |
| 1 | [pyspark, py4j] |
| 0 | [pytz, pandas] |
| 5 | [numpy] |
+----------+--------------------------------------------+
matplotlib社区被分割成为三个小社区：
- matplotlib, spacy, six, and python-dateutil
- pytz和pandas
- numpy
我们可以在图6-14中看到这个分解。
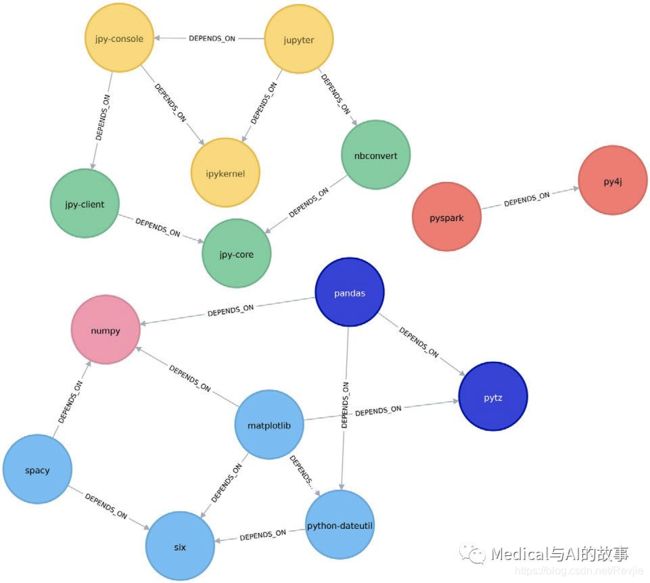
图6-14.Louvain算法发现的中间聚类
虽然这个图只显示了两层层次结构，但是如果我们在一个更大的图上运行这个算法，我们会看到一个更复杂的层次结构。Louvain揭示的中间集群对于检测可能无法被其他社区检测算法检测到的细粒度社区非常有用。
验证社区
社区检测算法通常有相同的目标：识别群体。然而，由于不同的算法从不同的假设开始，它们可能会发现不同的社区。这使得为一个特定的问题选择正确的算法变得更具挑战性，并且有点探索性。
与周围环境相比，当群体内的关系密度较高时，大多数社区检测算法都表现得相当好，但现实世界中的网络往往不那么明显。通过将我们的结果与基于已知社区数据的基准进行比较，我们可以验证所发现社区的准确性。
其中两个最著名的基准是Girvan-Newman (GN) 和Lancichinetti–Fortunato–Radicchi (LFR) 算法。这些算法生成的参考网络是完全不同的：GN生成一个更为均匀的随机网络，而LFR创建一个更为异构的图，其中节点度和社区大小根据幂律分布。
由于我们测试的准确性取决于所使用的基准，因此将我们的基准与数据集匹配是很重要的。尽可能多地寻找相似的密度、关系分布、社区定义和相关领域。
总结
社区检测算法对于理解节点在图中的分组方式很有用。在本章中，我们首先学习三角形计数和聚类系数算法。然后我们继续讨论两种确定性社区检测算法：强连接组件和连接组件。这些算法对社区的构成有严格的定义，对于在图分析管道的早期了解图结构非常有用。
我们完成了标签传播和Louvain模块化，这两个非确定性算法，它们能够更好地检测更细粒度的社区。Louvain还向我们展示了不同等级的社区。
在下一章中，我们将学习一个更大的数据集，并学习如何将这些算法组合在一起，以获得对所连接数据的更深入了解。