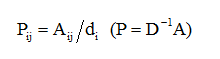网络社区划分的算法分类(2)
NP-hard问题
介绍NP困难之前要说到P问题和NP问题,P问题是在多项式时间内可以被解决的问题,而NP问题是在多项式时间内可以被验证其正确性的问题。 NP困难(NP-hardness, non-deterministic polynomial-time hardness)问题是计算复杂性理论中最重要的复杂性类之一。如果所有NP问题都可以多项式时间归约到某个问题,则称该问题为NP困难。
进化算法
进化算法(英语:Evolutionary Algorithm )是人工智能中进化计算的子集。进化算法启发自生物的演化机制,模拟繁殖、突变、遗传重组、自然选择等演化过程,对优化问题的候选解做演化计算的算法。
遗传算法
以遗传算法为例,其工作步骤可概括为:
(1) 对工作对象——字符串用二进制的0/1或其它进制字符编码。
(2) 根据字符串的长度L,随即产生L个字符组成初始个体。
(3) 计算适应度。适应度是衡量个体优劣的标志,通常是所研究问题的目标函数。
(4) 通过复制,将优良个体插入下一代新群体中,体现“优胜劣汰”的原则。
(5) 交换字符,产生新个体。交换点的位置是随机决定的
(6) 对某个字符进行补运算,将字符1变为0,或将0变为1,这是产生新个体的另一种方法,突变字符的位置也是随机决定的。
(7) 遗传算法是一个反复迭代的过程,每次迭代期间,要执行适应度计算、复制、交换、突变等操作,直至满足终止条件。
经典数据集
-
空手道俱乐部网络
-
海豚社会关系网络
-
美国大学生橄榄球联赛网络
-
Lesmis网络(《悲惨世界》)
-
PGP网络
-
纽曼科学合作网
-
Facebook社交网络数据集
-
DBLP合作网络和标注数据社区(合著者关系网)
-
谷歌网络图
人工数据集
-
GN基准网络
-
LFR基准网络
评价指标
传统基于图分割和谱分析的社区发现算法
1.Kernighan-Lin算法(KL算法)
交换不同社区中的节点,找到使割集规模变化量最大的顶点对
2.谱划分
基于图聚类的社区发现算法
1.基于划分的方法
2.基于层次的方法
计算每对节点间相似度
3.基于密度的方法
主要思想:只要邻近区域的密度(对象或者数据点的数目)超过了某个阈值,就继续聚类。
网络社区划分的算法分类
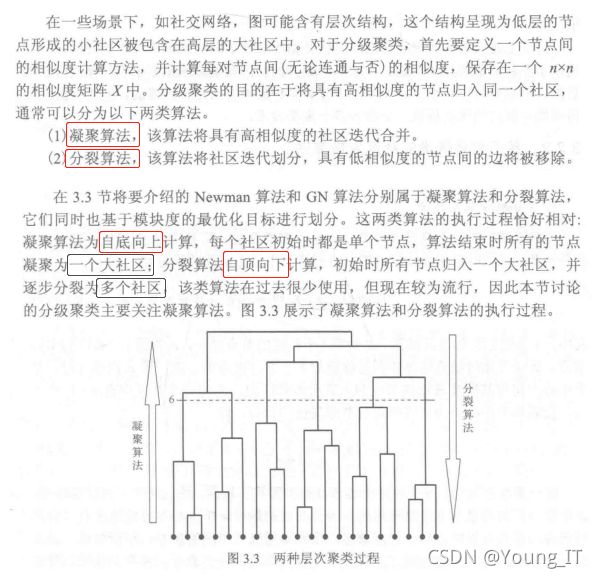
分裂层次方法的一般步骤:
-
采用某种度量计算节点相似度矩阵边的介数
-
删除相似度最低的边或介数最大的边
-
重新计算剩余网络的节点相似度矩阵边的介数
-
重复步骤和直到得到个非连通子图为网络的节点数目
凝聚层次策略的一般步骤:
-
把n个节点看成n类
-
计算节点(或节点集合)间的相似性矩阵
-
选择相似度最大的两个节点(或节点集合)合并为一类
-
重复步骤2和3直到最后所有节点组成一个大类
多目标优化
-
将传统的模块度函数划分为两部分作为两个互补的指标进行优化
-
模块度指标再加上其他评价标准优化
单目标优化——模块度最优化算法
1.基于K派系过滤的社团检测(基于物理模型)
相关基础概念:
K-派系(clique):网络中包含K个节点的全耦合子图,即K个节点中的任意两个节点之间都是相互连接的。
相邻:若两个K-派系中有K-1个公共节点,称这两个K-派系相邻。
连通:若一个K-派系可以通过若干个相邻的K-派系到达另一个K-派系,称其彼此连通。
K-派系社团:所有彼此连通的K-派系构成的集合,称为一个K-派系社团。
K-派系 代表 网络中的边(如3-派系为网络中的三角形)
K-派系社区 代表 彼此连通的K-派系的集合(3-派系社区为彼此连通的三角形的集合)
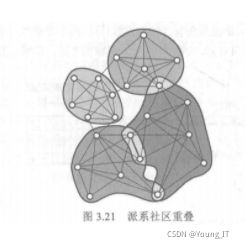
对上述网络进行K-派系过滤划分:
(1)在给定网络中找出所有规模为k=3的团,具体包括{1,2,3},{1,3,4},{4,5,6},{5,6,7},{5,6,8},{5,7,8},{6,7,8}。
(2)构建团图。若两个k团共享k-1即2个节点,那么将其连接起来。
连接1:{1,2,3},{1,3,4} 共享节点{1,3}。
连接2:{4,5,6},{5,6,7},{5,6,8},{5,7,8},{6,7,8}。
(3)每个连接的部分形成一个社区,得到两个社区C1={1,2,3,4},C2={4,5,6,7,8},其中节点4同时属于两个社区,因此为重叠节点。
2(聚合思想的算法)
2.1)基于fastgreedy算法的社团检测(模块度增量)
该算法的三个名称:CNM=fastgreedy=fastmodularity
算法原理:该算法以贪婪地最大化图的模块度的方式将单个节点合并到社区中。 可以证明,如果没有合并可以增加当前的模块度,则算法可以停止,因为无法进一步增加.
(1) 初始时将每个节点看作一个社团,每个社团中只有一个节点。
(2) 计算任意两社团合并对应Q值的增量,选择使Q值增加幅度最大的社团进行合并。
(3) 重复步骤(2)直到任意两社团合并都不能使Q值继续增加,Q值达到峰值。
该算法的性能优势:据说该算法在稀疏图上几乎以线性时间运行。
该算法存在的问题:Q最大值不一定是全局最优,可能是局部最优。
2.2)快速模块度优化算法——BGLL算法*
Louvain (BGLL) 算法[8]是一个基于模块度最优化的启发式算法,算法两层迭代,外层的迭代是自下而上的凝聚法,内层的迭代是凝聚法加上交换策略,避免了单纯凝聚方法的一个很大的缺点(两个节点一旦合并,就没法再分开)。
算法步骤:
Step1 每一个点初始时被看作一个社团, 按一定次序依次遍历每一个顶点.
对每一个顶点i ,考虑将 i 移至其邻居顶点 j 的社团中模块度的变化ΔQ 。
如果 ΔQ>0,将 顶点i 移至使得ΔQ变化最大的顶点的社团中;
否则,顶点 i 保持不动。重复这个过程,直到任何顶点的移动都不能使模块度增大。
Step2 将step1得到的每一个社团看作一个新的顶点,开始新的一轮迭代,直到模块度不再变化。
该算法简单、直观,容易实现;速度快,并且效果也很好。综合效率和效果两方面考虑,该算法应该是目前最好的方法之一。
2.3)MSG-VM算法*
(直接寻优算法)
极值优化EO算法
逐步达到最优
1.将网络划分为两个社区为目标,以顶点适合度判别需要调整的顶点。通过调整顶点属性,最后划分达到最优
2.再逐步增加社区
主要思想类似于生物系统演化中的断续平衡问题,之后用离散和连续的NPC问题,解决如图分割、伊辛模型、原子最优团簇结构等问题。
3.基于GN算法的社团检测(切割最大边介数)(分裂思想的算法)
算法基本思想:如果两个社区只是由少数几条边连接,那么两个社区之间的路径都要经过这几条边中的一条,因此边介数(edge betweenness)会很大。 利用边介数的概念,通过不断地切断边介数最大的边,获得层次性的社团结构。
算法的基本流程:
(1) 计算网络中每条边的边介数;
(2) 找出边介数最大的边,并将其移除;
(3) 重新计算网络中剩余各条边的边介数;
(4) 重复(2)和(3)步,直到网络中所有边都被移除,获得系统树图;
(5) 按照模块度函数Q值最大的原则,对系统树图进行切割,获得社区划分。
4.基于标签传播label propagation的社团检测LPA(标签传染:邻居节点最多标签)
算法基本原理:
1.为网络中每个节点分配一个不重复的标签label。
2.在每次迭代过程中,节点根据其所有邻居节点中出现次数最多的label更新自身label。如果最佳候选label超过一个,则在其中随机选择。
3.具有相同label的节点被归入同一个社区。
算法性能优势:在大多数情况下可以快速收敛。
算法性能缺陷:迭代的结果有可能不稳定,尤其在不考虑连边的权重时,如果社区结构不明显或者网络规模比较小时,有可能所有的节点都被归入同一社区。
标签传播算法尽管速度快,但是效果并不太理想。
5.基于拉普拉斯矩阵的特征向量Leading eigenvector的社团检测**
算法基本原理:
拉普拉斯矩阵L = 度矩阵(degree matrix)D - 邻接矩阵(adjacency matrix)A
L中最小的特征根总等于0,而L的特征根中0的个数即为无向网络G中社区的个数,因此如果除了最小特征根没有别的特征根为0,则整个网络构成一个整体。
第二小的特征根(或者最小的非零特征根)又叫做代数连通性(algebraic connectivity),其对应的特征向量叫做Fidler vector。
根据Fidler vector特征向量值中元素取值进行社区划分。
6.基于层次聚类multilevel的社团检测(模块度标准)
算法基本原理:
层次聚类为一种自底向上的算法,初始化时定义每个节点归属于一个分离的社区,根据总体社区划分模块度最大化的原则,以迭代的方式最大化每个节点社区移动所带来的局部贡献。
算法基本过程:
(1) 将每个节点当作一个社区。
(2) 基于模块度标准决定哪些邻居应该被合并。经过一次迭代之后,一些社区合并为一个社区。
(3) 每个社区被当作一个节点,对其度和连接信息进行统计,基于统计结果再进行下一次迭代合并。
(4) 重复步骤(3)直到网络社区划分对应的总体模块度不能再增加为止。
7.基于community_optimal_modularity算法的社团检测
8.基于随机游走walktrap的社团检测**
P. Pons 和 M. Latapy 2005年提出了基于随机游走的网络社区划分算法,使用两点到第三点的流距离之差来衡量两点之间的相似性,从而为划分社区服务。
算法具体操作步骤:
1.对网络G的邻接矩阵A按行归一化D.^(-1)*A得到概率转移矩阵(transition matrix)P,D是度矩阵。利用P矩阵的马可夫性质可知,它的t次方的元素Pijt就代表着随机游走的粒子经过t步从节点i到j的概率。
2.定义两点ij间的距离如下:其中t是流的步长,k是某一目标节点。步长t必须恰当选择,因为如果t太小,不足以体现网络的结构特征;如果t太大,则Pijt趋近于与j的度数d(j)成正比,出发点i的拓扑信息被抹去。t经验值为2到5之间。
随机游走: 从一个顶点向下一个顶点移动时,以相等的概率来选择当前顶点的一个邻居作为下一个顶点。
基本思想: 社团相对比较稠密的子图,因此在图中进行随机游走时很容易“陷入”一个社团中。
随机游走的过程构成了一个Markov链。图中每一个顶点对应一种状态;不同状态之间的转移概率为
t 步随机游走从 i 到 j 的概率是 Pij 的t次幂
下面我们介绍一个代表性的随机游走算法,叫做Walktrap 算法[7]
9.基于community_spinglass算法的社团检测
10.基于infomap的社团检测(推测随机游走粒子,求‘平均流’)
算法核心思想: 好的社区划分要令网络上流的平均描述长度最短。
分析有向加权网络的一个好的视角是观察某类实体(货币、能量、信息)在网络上的流动,即使没有实体流动的数据,也可以根据网络的基本结构来推测随机游走粒子的轨迹,然后对得到的“平均流”进行信息编码。对“平均流”描述长度最短的编码机制,就对应着对社区的一种最有效划分。
12.K-Means
基本思想是首先找各个社团的“中心点”, 然后就近分配每个顶点
算法步骤:选取k个点作为 k个社团的初始中心点
Step1. 把每个点分配到最近的中心点所在的社团
Step2. 重新计算中心点,如果中心点不变, stop; 否则, 转 step1.
K-Means算法计算量相对比较大,效果往往还不错,但是使用前要考虑一点:通过各个分量求平均得到的中心点是否有意义, 也就是说在你的问题中欧式距离是否有意义。
13. Canopy算法
思想:选择计算代价较低的方法计算相似性,将相似的对象放在一个子集中,这个子集被叫做Canopy,不同Canopy之间可以是重叠的
算法步骤:
Step1 设点集为 S,预设两个距离阈值 T1和 T2(T1>T2);
Step2 从S中任选一个点P,用低成本方法快速计算点P与所有Canopy之间的距离,将点P加入到距离在T1以内的Canopy中;如果不存在这样的Canopy,则把点P作为一个新的Canopy的中心,并与点P距离在 T2 以内的点去掉;
Step3 重复step2, 直到 S 为空为止。
该算法精度低,但是速度快,常常作为“粗”聚类,得到一个k值,再用k-means进一步聚类,不属于同一Canopy 的对象之间不进行相似性计算。