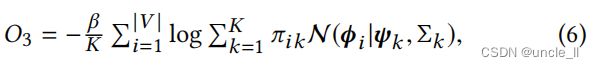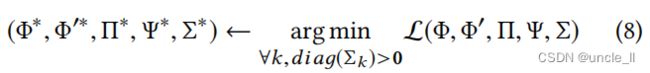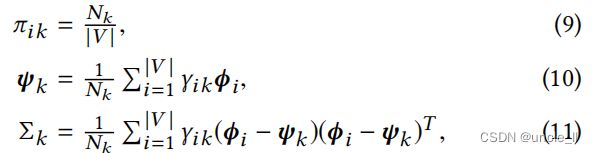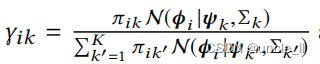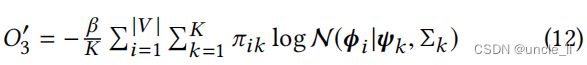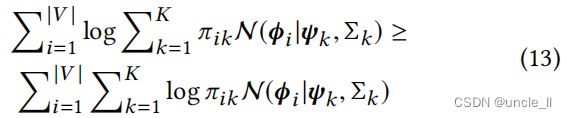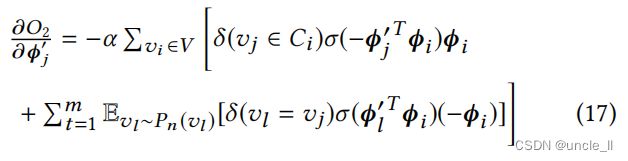Learning Community Embedding with Community Detection and Node Embedding on Graphs

Learning Community Embedding with Community Detection and Node Embedding on Graphs

在图上学习社区嵌入与社区检测和节点嵌入

• 作者：Sandro Cavallari， Vincent W. Zheng， Hongyun Cai， Kevin Chen-Chuan Chang， Erik Cambria
• 单位：Advanced Digital Sciences Center, Nanyang Technological University

• 论文地址： http://sentic.net/community-embedding.pdf
• 项目地址：https://github.com/andompesta/ComE

摘要

在本文中，研究了一个重要的但在很大程度上尚未被探索的图嵌入设置，即嵌入社区而不是每个单独的节点。我们发现，社区嵌入不仅适用于图形可视化等社区级应用程序，而且有利于社区检测和节点分类。为了学习这种嵌入，本文的见解取决于社区嵌入、社区检测和节点嵌入之间的一个闭环。另一方面，节点嵌入有助于提高社区检测能力，输出良好的社区，以拟合更好的社区嵌入。另一方面，社区嵌入可以通过引入具有社区感知能力的高阶邻近性来优化节点嵌入。基于此，本文提出了一个新的社区嵌入框架，共同解决这三个任务。并在多个真实数据集上评估了这样一个框架，并表明它能够改进图形可视化，并在各种应用程序任务中优于最先进的基线，例如，社区检测和节点分类。

论文分类索引

• Computing methodologies → Neural networks;
• Machine learning algorithms;
• Mathematics of computing → Probabilistic algorithms；
• Applied computing → Sociology;

关键词

• community embedding
• graph embedding

1 介绍

传统上，图嵌入侧重于单个节点，其目的是输出图中每个节点的向量表示，这样图上的两个节点“相近”的话，在低维空间中具有相似的向量表示。这种节点嵌入在保持网络结构方面非常成功，并显著改进了广泛的应用范围，包括节点分类（node classification）[5,20]、节点聚类（node clustering）[27,34]、链路预测（link prediction）[12,19]、图形可视化（graph visualization）[24,29]及更多[10,18]。

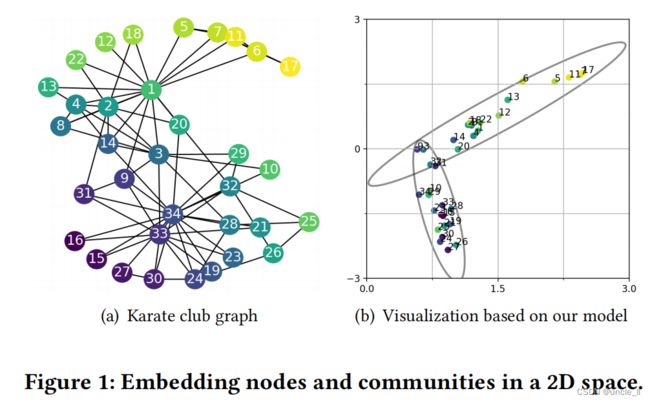
在本文中，我们研究了另一个重要的，但在很大程度上开发不足的图的嵌入，它的重点是社区嵌入。一般来说，“社区嵌入”是在低维空间中对社区的表示。由于社区是一组紧密连接的节点，因此期望通过嵌入社区来描述其成员节点在低维空间中的分布方式。因此，我们不能简单地将一个社区嵌入定义为一个向量；相反，需要将它定义为低维空间中的一个分布。在图1中，使用常见数据集空手道俱乐部为例，来演示在二维空间中的社区嵌入。如图1(a)所示，空手道俱乐部图有34个节点和78条边。众所周知，这个图有两个社区，一个由一个俱乐部讲师（节点1）联络，另一个由一个俱乐部管理员（节点34）联络；一些俱乐部成员（如节点9）被确定为这两个社区的“弱支持者”，因此他们可以同时属于这两个社区。在图1(b)中，将图1（a）可视化在二维空间中，其中每个节点的嵌入都是一个二维向量。

由于每个社区都是一组紧密连接的节点，本文受到高斯混合模型(GMM)[3]的激励，将每个社区嵌入视为二维空间中的多元高斯分布。因此，我们将空手道俱乐部图中的两个重叠社区可视化为两个重叠的月食，每个社区都有一个二维平均向量和一个2×2协方差矩阵。社区嵌入对于许多社区级别的应用程序很有用，例如，社区可视化帮助从大图中生成见解，或者社区建议搜索类似的社区。

学习社区嵌入是比较重要的。一方面，为了获得有意义的社区嵌入，首先需要很好地识别社区；然后，社区嵌入的一个直接的方法是：

• （1）在图上运行社区检测，如谱聚类（Spectral Clustering）[25]，以获得每个节点的社区分配；
• （2）应用节点嵌入，如DeepWalk[20]或LINE[24]，在图上得到每个节点的嵌入向量；
• （3）将每个社区中的节点嵌入向量进行聚合，从而拟合一个（多元高斯）分布作为其社区嵌入；

这种管道方法是次优的，因为它的社区检测是独立于其节点嵌入的。另一方面，最近的研究表明，由于节点嵌入能够很好地在低维空间中保持网络结构，因此它通常可以提高社区检测能力。因此，另一种可能的社区嵌入方法是直接对节点嵌入结果运行社区检测。因此，根据每个社区的节点嵌入向量拟合一个（多元高斯）分布。然而，这种方法也是次优的，因为大多数现有的节点嵌入方法(如DeepWalk[20]、LINE[24]和Node2Vec[12])都不知道社区结构，这使得它们的节点嵌入输入对于后续的社区检测并不理想。在第5节中，我们对上述两种方法进行了实验评估，并表明它们的性能是有限的。很少有工作将节点嵌入和社区检测放在一起考虑；它们要么需要额外的监督（例如，must-links）[34]，要么需要高计算复杂度（例如，图中节点数的二次方）[31]。此外，他们没有在低维空间中将一个社区描述为一个向量，因此很难准确地可视化重叠的社区。

我们对学习社区嵌入的认识是，在社区检测、社区嵌入和节点嵌入之间存在一个闭环，如图2所示。

一方面，如前所述，节点嵌入可以帮助提高社区检测（即①），从而输出良好的社区来拟合有意义的社区嵌入（即②），另一方面，社区嵌入可以用于优化节点嵌入（即③）。假设对于一个社区k，我们已经将它的社区作为一个多元分布嵌入到一个低维空间中，然后可以强制社区k的成员节点紧密地分散在其低维空间的社区嵌入的平均向量附近。因此，这些相同的社区节点往往具有相似的节点嵌入向量。与一级二阶近似相比，社区嵌入不需要两个节点直接连接或共享许多“上下文”来接近。由于社区中两个节点之间的连接可以是高阶的，因此我们认为社区嵌入是引入了对节点嵌入的社区感知的高阶接近。从社区嵌入到节点嵌入的反馈帮助我们关闭循环；希望社区感知的节点嵌入可以作为后续社区检测的更好的输入，从而产生更有意义的社区嵌入结果。

在闭环洞察力的指导下，本文提出了ComE算法，一个新的社区嵌入框架，共同解决了社区嵌入、社区检测和节点嵌入等问题。我们将社区嵌入定义为多元高斯分布，并利用它通过高斯混合公式对节点嵌入结果进行社区检测。图一般表示为G=(V，E)，其中V是节点的集合，E是边的集合。高斯混合公式使我们能够有效地检测社区，并从O(|V|)时间内的G推断其社区嵌入分布。给定社区分配和社区嵌入，扩展了DeepWalk和LINE的神经网络公式，以保持第一、二阶和高阶（社区感知）的接近性。对于这个神经网络公式，提出了一个可伸缩的推理算法，其复杂度与图大小呈线性关系$O(|V|+|E|)$。本文的贡献如下：

• 引入了一种新的联合建模框架，它利用节点嵌入、社区检测和社区嵌入之间的闭环来学习图的嵌入
• 提供了一个可扩展的推理算法，其中O(|V|+|E|)的复杂性通常低于现有的高阶接近感知方法(如表1)
• 在具有不同应用程序任务的多个真实数据集上评估ComE算法。它提供了更好的图形可视化结果，并在社区检测中提高了至少6.6%(NMI)和2.2%–16.9%（conductance），在节点分类中提高了0.8%–26.9%(macro-F1)和0.71%-48%(micro-F1)

2 相关工作

在表1中总结了一些具有代表性的图嵌入和社区检测工作的差异。接下来，将详细讨论相关的工作

2.1 图嵌入

随着图数据数量的增加，从社交网络到各种信息网络，一个重要的问题出现了，即如何为表示一个图用于分析[11]。图嵌入是最先进的图表示框架，旨在将图投影到低维空间，用于进一步应用[16,20,26]。在要嵌入的目标方面，现有的图嵌入方法大多集中在节点上。例如，早期的方法，如MDS[7]，LLE[21]，IsoMap[26]和拉普拉斯特征映射[2]，旨在保持提取图相似矩阵（亲和矩阵衡量一个空间中两点的距离或者相似度）的主要特征向量的一阶接近性。（affinity matrix表示点与边之间的关系，adjacent matrix表示点与点之间的关系）

最近的方法开始利用神经网络来学习每个节点的表示，可以使用浅层架构[12,24,33]或深层架构[1,8,18,29]。DeepWalk[20]对路径采样节点嵌入的二阶近似度进行建模，使用分层softmax进行推理的复杂度为$O(|V|log|V|)$。Node2Vec[12]通过控制路径采样过程扩展了DeepWalk，复杂度为$O(|V|a^2)$，其中a是图的平均度；因此，它的模型复杂度为$O(|V|log|V|+|V|a^2)$。LINE[24]和SDNE[29]以更高的复杂度保持了第一级二阶接近，分别为O(a|E|)和O(a|V|)。

与我们的方法相比，上述工作的复杂性较低或可比较，但没有试图检测或代表社区。社区结构是一种重要的网络属性，在节点嵌入中已被考虑。例如，在SAE[27]中，作者表明，谱聚类（ spectral clustering）可以看作是重建一个图的归一化相似度矩阵，但它代价昂贵，复杂度至少为$O(|V{|}^2.367)$。因此，他们提出直接构造具有$O(|E|)$复杂度的归一化相似度矩阵，并将其输入到堆叠的自动编码器中，以具有$O(|V|)$复杂度进行重构。所得到的节点嵌入用于K-means聚类，结果表明比谱聚类获得更好的社区。类似地，DNR[34]从具有$O(|V{|}^2)$复杂度的图中构造一个模块化矩阵，然后将堆叠的自动编码器应用于模块化矩阵进行节点嵌入，它还引入了必须链接来监督节点的嵌入。

高阶的接近方法，如GraRep[5]和HOPE[19]，并没有明确的社区意识。除此之外，GraRep学习一个高阶转移概率矩阵，然后以$O(|V{|}^3)$复杂度运行奇异值分解(SVD)。上述方法既没有尝试嵌入社区，也没有显式地在节点嵌入中检测社区，但由于实际工作网络的稀疏性，通常具有较高的复杂性。很少有工作试图显式地将社区嵌入到低维空间中。例如，M-NMF[31]构造具有$O(|V{|}^2)$复杂度的模块化矩阵，然后应用非负矩阵分解来学习节点嵌入和社区检测，以及与$O(|V{|}^2)$成比例的复杂度。

相比之下，M-NMF用一个向量表示每个社区，但是我们不会认为它产生一个社区嵌入；而且它的复杂性通常高于本文的O(|V|+|E|)，因为在实际中，图是稀疏的，$|E|\ll |V{|}^2$。

2.2 社区检测

社区检测的目的是在图中发现节点组，这样的组内连接比组间连接[30]更密集。随着社交网络的普及，最近的社区检测研究开始利用图上丰富的节点交互，如具有内容[22]的节点、属性[23]和节点到节点的扩散[4]。在[32]中可以找到对最近的社区检测算法的全面调查。在这项工作中，我们的社区检测被应用于同构图，它们的节点和边没有额外的信息。早期的同构图上的社区检测方法经常直接对图的邻接矩阵应用不同的聚类算法。例如，在[25]中，将谱聚类应用于社交网络来提取社区。在[13]中，训练一个拉普拉斯正则化的GMM来捕获最近邻图的流形结构。

随着神经网络和深度学习的发展，节点嵌入被用于辅助社区检测[15,27]。这种工作通常首先将图嵌入到低维空间中，然后对嵌入结果应用K-means等聚类算法。尽管这些基于节点嵌入的方法在检测社区方面取得了成功，但它们往往没有联合优化节点嵌入和社区检测。由于它们的目标主要是社区检测，因此它们不一定有明确的社区嵌入概念。

3 问题公式化

作为输入，给出了一个图$G=(V，E)$，其中V是节点集，E是边集。传统的图嵌入的目的是学习每个$vi\in V$的节点嵌入，即${\varphi }_i\in R^d$。在本文中，也尝试学习社区嵌入。假设图g上有K个社区。对于每个节点$v_i$，我们将其社区分配表示为$z_i\in 1，...，K$。

受高斯混合公式[3]的启发，本文将社区嵌入定义为低维空间中的多元高斯分布。

定义3.1。社区k(与$k\in 1，...，K$)在d维空间中的社区嵌入是一个多元高斯分布$N(\psi k，\Sigma k)$，其中$\psi k\in R^d$是一个均值向量，$\Sigma k\in R^{d\times d}$是一个协方差矩阵。

作为输出，我们的目标是学习：

• （1）节点嵌入${\varphi }_i$为每个节点$v_i\in V$；
• （2）社区成员${\pi }_{ik}$，为每个节点$v_i\in V$和每个社区$k\in 1，...，K$；
• （3）每个社区$k\in 1，...，K$，社区嵌入参数 $({\psi }_k,\Sigma k)$

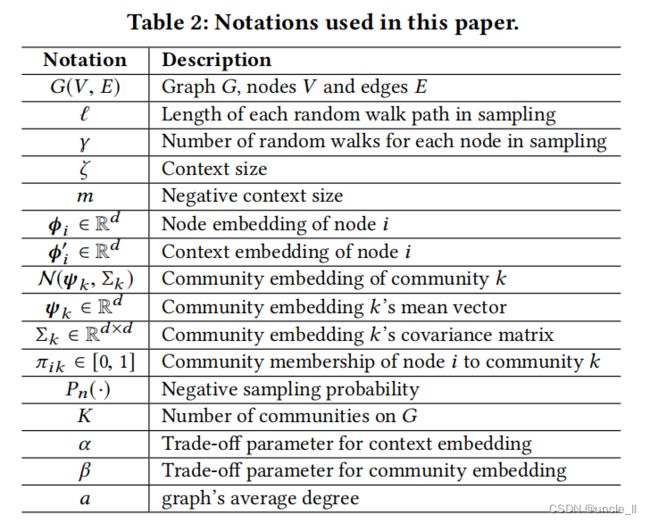
本文的一些符号如表2所示：

3.1 社区检测和嵌入

给定节点嵌入，检测社区并学习其社区嵌入的一种直接方法是采用管道（pipeline）方法。例如，如图2所示，可以运行谱聚类来检测社区，然后对每个社区拟合一个高斯混合。但是，这种管道方法缺乏统一的目标函数，因此很难通过节点嵌入进行优化。或者，也可以将社区检测和嵌入到一个基于GMM的单一目标函数中。也就是说，我们认为每个节点$v_i$的嵌入${\varphi }_i$是由一个社区$z_i=k$的多元高斯分布生成的。然后，对于V中的所有节点，我们有这样的可能性为

其中，$p(z_i=k)$为节点$v_i$属于社区k的概率。为了简单表示，将$p(z_i=k)$表示为${\pi }_{ik}$，因此，我们有${\pi }_{ik}\in [0,1]$和$sigma{\pi }_{ik}=1$。在社区检测中，这些${\pi }_{ik}$表示每个节点$v_i$的混合社区成员度，它们是未知的。另外，$p(v_i|z_i=k；{\varphi }_i，{\psi }_k，\Sigma k)$是一个多元高斯分布，定义如下

在社区嵌入中，$({\psi }_k，{\Sigma }_k)$的情况是未知的。通过优化等式1${\pi }_{ik}$和$({\psi }_k，{\Sigma }_k)$，同时实现了社区检测和嵌入。

3.2 节点嵌入

传统上，节点嵌入侧重于保持一阶或二阶的接近性。例如，为了保持一阶接近性，LINE[24]通过最小化来强制两个相邻节点具有相似的嵌入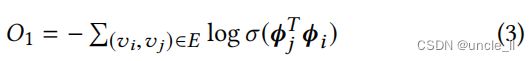

其中$\sigma (x)=1/(1+exp(-x))$是一个s型函数。为了保持二阶邻近性，LINE和DeepWalk[20]都强制两个节点共享许多“上下文”（即ζ跳中的邻居）以具有相似的嵌入。在这种情况下，每个节点都有两个角色：一个针对自身的节点和一个针对其他节点的上下文。为了区分这些角色，DeepWalk为每个节点$v_j$引入了一个额外的上下文嵌入，作为$\varphi j‘\in R^d$，使用$Ci$表示$v_i$的上下文集合。

然后，本文采用负采样[17]来定义一个函数，以衡量$v_i$生成每个上下文$v_j\in C_i$的效果：

其中，$v_l\sim Pn(v_l)$表示根据概率$Pn(v_l)$采样一个节点$v_l\in v$作为$v_i$的“负上下文”。我们根据[17]中那样设置$Pn(vl)\propto r_l^3/4$，其中$r_l$为$v_l$的度。总的来说，有m个负的上下文。一般来说，使等式最大化等式4强制节点$v_i$的嵌入${\varphi }_i$以最好地生成它的正上下文${\varphi }_j$，而不是生成它的负上下文${\varphi }_l$。然后，可以最小化以下目标函数，以保持二阶接近性：

其中，α>0是一个权衡参数。

3.3 关闭循环

为了关闭图2中的循环，我们需要实现从社区检测和社区嵌入到节点嵌入的反馈。假设已经在3.1部分确定了混合社区成员${\pi }_{i}k$和社区嵌入(ψk，Σk)。然后可以使用再次使用公式1去获得反馈。最优化公式1，强制使得ϕi同一社区中的节点ϕi更接近相应的社区中心ψk， 即，共享一个社区的两个节点很可能有类似的嵌入。与一阶和二阶接近相比，该设计在节点嵌入上增强了社区感知的高阶接近，这对以后的社区检测和嵌入非常有用。与一阶和二阶近似相比，该设计在节点嵌入上增强了社区感知的高阶接近，这对以后的社区检测和嵌入非常有用。例如，在图1(a)中，节点3和节点10是直接连接的，但根据[35]，它们往往属于两个不同的社区。因此，通过只保持一阶相似性，我们可能不能很好地告诉他们的社区成员的差异。对于另一个例子，节点9和节点10共享一些一跳和两跳邻居，但与节点10相比，根据[35]，节点9往往更接近由节点1领导的社区。因此，通过只保持二阶接近性，可能也不能很好地告诉他们的社区成员的差异。

在闭环优化的基础上，将社区检测、社区嵌入和节点嵌入共同进行了优化。我们有三种类型的接近，包括一阶、二阶和高阶接近。一般，有两种方法结合不同类型的节点嵌入：

• （1）“concatenation”，像LINE中首先分别优化O1和O2，然后将每个节点的两个结果嵌入结果连接到一个长向量中作为最终输出；
• （2）“unification”， SDNE[29]为每个节点学习单个节点的嵌入，以同时保持一阶和二阶的近似性。

在本文中，为了鼓励节点嵌入来统一多种类型的近似性，我们采用了统一的方法，并将另一种方法作为未来的工作。因此，基于等式1， 我们定义了社区检测和嵌入的目标函数，并强制执行节点嵌入的高阶近似性为

其中，$\beta \ge 0$是一个权衡参数。对于$i=1，...，|V|$和$k=1，...，K$有$\Phi =\varphi i$，$\Phi \prime =\varphi \prime i$，KaTeX parse error: Expected '}', got 'EOF' at end of input: Π={π_{ik}，$\Psi =\psi {\prime }_k$和$\Sigma =\Sigma k$。

然后，我们统一了节点嵌入的一阶和二阶接近性。ComE的最终目标函数是

最后的优化问题是：

其中，$diag(\Sigma k)$返回$\Sigma k$的对角线项。我们对每个$k\in 1，...，K$特别引入了$diag(\Sigma k)>0$的约束，以避免优化L的奇异性问题。类似于GMM[3]，存在无任何约束的优化L的退化解。也就是说，当一个高斯分量坍缩到一个单点时，$diag(\Sigma k)变为零$，这使得O3变为负无穷大

4 推理

因为等式8的目标可以看作是由节点嵌入和社区嵌入组成的，我们将优化分解为两部分，并采用迭代的方法来求解它。具体地说，考虑在给定约束最小化$（\Phi ，\Phi ‘）$迭代优化$（\Pi ，\Psi ，\Sigma ）$和在给定无约束最小化的$（\Pi ，\Psi ，\Sigma ）$迭代优化$（\Phi ，\Phi ’）$。经经验证明，该迭代优化算法在合理的初始化条件下收敛迅速。例如，我们在实验中通过DeepWalk结果初始化$（\Phi ，\Phi ‘）$，在Sec5.4中报告了收敛性。接下来，我们将详细介绍这个迭代优化。

**固定$(\Phi ,\Phi \prime )$, 优化$ (Π, Ψ, Σ)$\ast \ast ,在这种情况下，等式8被简化为推断a，对每个$k∈{1，…，K}$使用$diag(Σk)>0$的约束。为了解决这种约束优化，采用了[3]提出的方法，即使用\ast \ast 期望最大化(EM)\ast \ast 算法[9]来推断$（Π，Ψ，Σ）$，并在$diag(Σk)$开始为零时，通过随机重置$Σk>0$和$ψk∈R^d$的适当启发式来满足约束。特别是，通过EM，可以迭代更新$（Π，Ψ，Σ）$

其中：

值得注意的是，在实践中，如果$（\Phi ，\Phi ‘）$被合理地初始化(例如，在实验中通过DeepWalk)，则很容易满足$diag(\Sigma k)>0$的约束，因此$（\Pi ，\Psi ，\Sigma ）$的推理可以快速收敛。

**固定$ (Π, Ψ, Σ)$，优化$(Φ, Φ′)$\ast \ast ，在这种情况下，等式8被简化为对具有三种接近类型的节点嵌入的无约束优化。由于在O3的对数项内求和，很难计算$ϕ_i$的梯度。因此，试图最小化L的上界$L（Φ，Φ‘|Φ，Ψ，Σ）$来作为代替。具体来说，引入：

很容易证明$O‘3（\Phi |\Pi ，\Psi ，\Sigma ）\ge O3（\Phi |\Pi ，\Psi ，\Sigma ）$, 这是由于下面的对数凹函数：

因此，我们就这样定义了

因此，即$L‘（\Phi ，\Phi ’|\Pi ，\Psi ，\Sigma ）\ge L（\Phi ，\Phi ‘|\Pi ，\Psi ，\Sigma ）$。通过随机梯度下降(SGD)[17]来优化$L‘（\Phi ，\Phi ’）$。对于每一个$v_i\in V$，都有

我们还计算了上下文嵌入的梯度为

算法和复杂度

我们在Alg1中总结了ComE的推理算法。 在第1行中，对于每个$v_i\in V$，我们从G上长度为$\ell$的$v_i$开始采样$\gamma$路径。在第2行中，通过DeepWalk初始化$（\Phi ，\Phi ‘）$。在第4-8行中，固定$（\Phi ，\Phi ’）$并优化$（\Pi ，\Psi ，\Sigma ）$用于社区检测和嵌入。在第9-16行中，固定$（\Pi ，\Psi ，\Sigma ）$并优化$（\Phi ，\Phi ‘）$以进行节点嵌入。

特别是，通过一阶接近（第9-10行）、二阶接近（第11-14行）和社区感知的高阶接近（第15-16行）来更新节点嵌入。

**分析Alg1的复杂性。**第1行的路径采样复杂度为$O(|V|\gamma \ell )$。在第2行参数初始化deepwalk复杂度为$O(|V|)$。在第5行t社区检测和嵌入复杂度为$O(|V|K)$, 第6-8行中检查约束条件复杂度为$O(K)$。第9-10行的节点嵌入一阶近似复杂度为O(|E|)，第11-14行的节点嵌入二阶近似复杂度为$O(|V|\gamma \ell )$，第15-16行的社区高阶近似需要$O(|V|K)$, **总的复杂性为$O(|V|\gamma \ell +|V|+T1\times (T2|V|K+K+|E|+|V|\gamma \ell +|V|K))$。**它与图的大小是线性相关得到(即|V|和|E|)。因此，Alg1是有效的。

5 实验

由于社区嵌入有助于低维空间中的社区可视化，也有助于社区检测和节点嵌入，因此我们为实验设计了三个评估任务：图形可视化、社区检测和节点分类。此外，还对本节的模型收敛性和参数敏感性进行了实证研究。 代码链接：https://github.com/andompesta/ComE.git

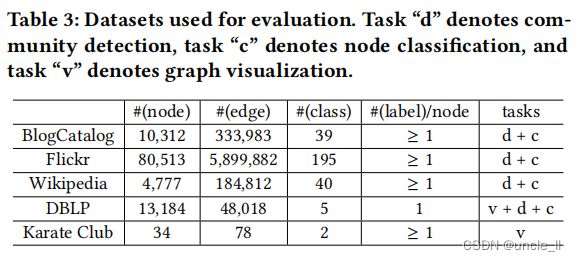
数据集：使用五个公共图数据集进行评估。这些图有各种类型，从社交网络到单词共现网络和学术论文引文网络：

• BlogCatalog： 是一个供用户发布博客的社交网络。在这个数据集中，每个节点都是一个博客目录用户，每条边都是一个友谊连接。每个节点都有多个标签，指示用户的博客主题的主题。
• Flickr：是一个供用户分享图片和视频的社交网络。在这个数据集中，每个节点都是一个Flickr用户，每条边都是一个友谊连接。每个节点都有一个标签，指示用户的兴趣组，如“海洋探险家”。
• Wikipedia：是一个出现在维基百科转储的第一百万字节中的单词的共现网络。在这个数据集中，每个节点都是一个单词，每条边都是一个单词的共现关系。每个节点都有一个标签，表示单词的词性标签。
• DBLP： 是一个建立在DBLP存储库基础上的学术论文引文网络。从5个领域的19个会议中提取了论文，如Tab4所示。 在这个数据集中，每个节点都是一张论文，每条边都是一个引文。每个节点都有一个标签，表示其论文会议地点的五个区域之一。
• Karate Club： 是一个大学空手道俱乐部[35]的社交网络。

在Tab3中总结了每个数据集的统计数据和评估任务。

评估指标

• 在社区检测中，同时使用电导系数（conductance）[14]和归一化互信息(NMI)[27]。电导系数基本上是离开社区的边数与社区内的边数之间的比率。NMI测量节点真实标签与预测社区之间的紧密度。

• 在节点分类中，使用了micro-F1和macro-F1 [20]。MicroF1是整体的F1各种各样的标签。macro-F1每种标签F1分数的平均值。

Baselines：设计baseline来支持我们的论点, 学习社区嵌入很重要。

• SF: 我们首先设计了一种简单的方法来分离社区检测和节点嵌入，然后从检测和节点嵌入结果中拟合社区嵌入。使用谱聚类[25]进行社区检测，并使用DeepWalk进行节点嵌入；最后，使用GMM来拟合社区嵌入。请注意，由于它的节点嵌入与DeepWalk相同，这里将只在空手道数据集的社区检测和社区可视化中评估SF。

此外，还考虑了另一种方法，即根据以下最先进的基线对节点嵌入结果运行社区检测，然后运行GMM来检测社区并拟合社区嵌入。

• DeepWalk[20]：它在嵌入过程中建模二阶接近。
• LINE[24]：它同时考虑一阶和二阶接近性。
• Node2Vec[12]：它通过利用嵌入中的同质性和结构作用，扩展了DeepWalk。
• GraRep[5]：它模拟了基于高阶近似的随机游走。

将我们的模型与所有数据集上的所有基线进行了比较。然而，由于像GraRep, M-NMF这样的基线，经常需要计算密集的邻接矩阵，在运行这些基线时遇到了即使使用Flickr数据集也会遇到64gb内存不足的错误。同样，Node2Vec在Flicker上也是不可行的，因为它必须计算和存储每个节点的每个邻域的转移概率，以便对离散分布进行非均匀采样。

参数和环境。本文提出的ComE只比DeepWalk多两个参数（即α和β）。为了获得一个公平的比较，遵循DeepWalk和Node2Vec的工作来设置参数。除非另有说明，对于所有的方法，设置嵌入维数d=128。对于DeepWalk、Node2Vec和ComE，设置了$\gamma =\zeta =10$、$\ell =80$和$m=5$。作为我们的方法，Node2Vec还提供了另外两个需要调优的参数。对于BlogCatalog和Wikipedia，我们遵循[12]中所做的工作，其中$p=0.25$和$q=0.25$的结果是对BlogCatalog的最佳调优。而Wikipedia在使用$p=4$和$q=1$时表现得更好。我们也遵循了与DBLP相同的调优过程，我们发现, 和BlogCatalog一样，$p=0.25$和$q=0.25$时候效果最好。对于M-NMF，我们在[0.1, 1, 5, 10]范围内调整α和β，同时保持其他参数不变。最后的设置是：BlogCatalog和Wikipedia的（1）α=0.1和β=5；（2），而对于DBLP，使用α=10和β=5。对于所有的数据集，设置K为唯一标签的数量。

使用8台3.50 GHz的IntelXeon®cpu和16GB内存的Linux机器上进行了实验

5.1 图可视化

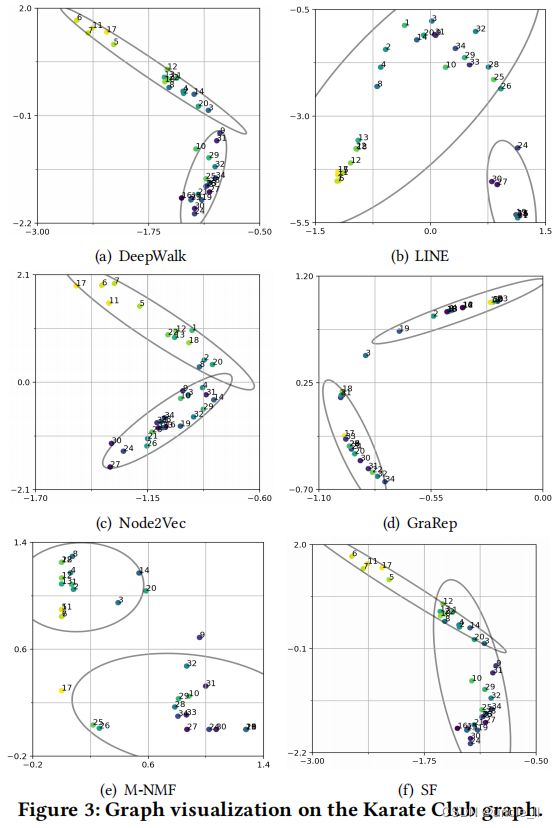
我们在小的空手道俱乐部和一个大的DBLP论文引文图上进行了基线的比较。基于基线的节点和社区嵌入结果，我们可视化了空手道俱乐部图，如图3所示。

正如所看到的，LINE并没有呈现社区结构，因为它在其节点嵌入中没有考虑到社区。DeepWalk、Node2Vec、GraRep和M-NMF倾向于呈现两个独立的社区，但是它们不能识别那些弱支持者（例如，节点9），而SF则由于谱聚类而检测噪声社区。相比之下，如图1(b)所示，ComE通过对重叠社区检测、社区嵌入和节点嵌入的联合建模，可以清晰地识别出这种弱支持者。

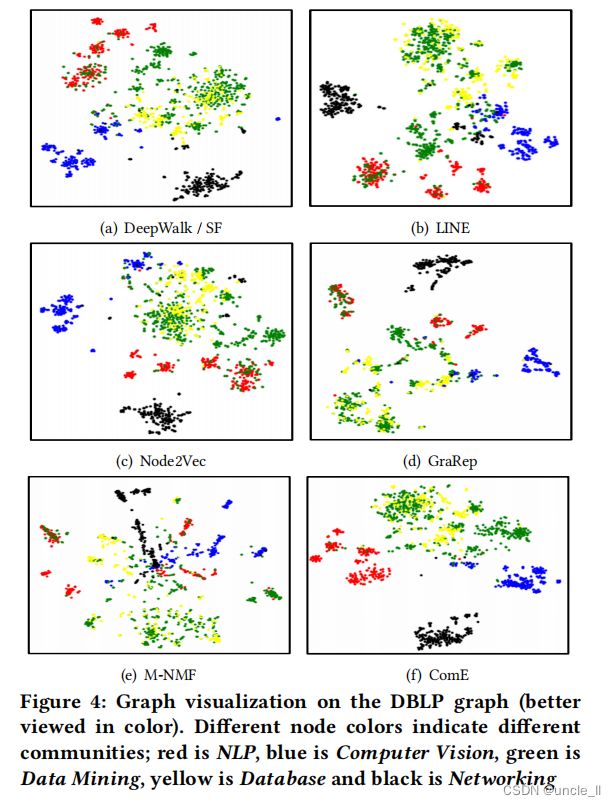
在图4中可视化了DBLP论文的引文图。使用t-SNE工具包[28]来进行图形可视化。在t-SNE中，使用不同的节点颜色来可视化不同的社区，看看算法是否能够正确保存图中出现的社区，而不是绘制嵌入社区的重叠。需要注意的是，虽然SF和DeepWalk生成社区嵌入的方式不同，但它们使用相同的节点嵌入，因此它们的可视化结果如图4(a)。所示首先，请注意，没有一种方法能够分离绿色类和黄色类（数据挖掘和数据库），我们认为这与数据集本身有关，因为这两个主题的相似性。此外，DeepWalk和Node2Vec生成的表示与颜色之间有许多重叠，整体嵌入非常相似。这是可能的，因为这两种方法的模型都只有二阶接近。

LINE呈现了一个更有凝聚力的可视化；这可能是由于它保持一阶和二阶接近的能力。我们还观察到，在GraRep的研究结果中，绿色的节点分布在不同的地方，并与红色和黄色的节点混合，这意味着在嵌入的过程中缺乏清晰的群落结构。这是可能的，因为它能够分解一个高阶转移概率矩阵，可能是被数据挖掘和数据库节点所主导。另一方面，它能够正确地检测网络和计算机视觉社区。相反，M-NMF呈现出模糊的社区结构，由于M-NMF通过学习模块化矩阵来学习社区的嵌入，这可能是由于绿色和黄色节点重叠而产生的噪声。这一假设也得到了空手道数据集结果的支持(图3(e))，其中M-NMF已经证明在建模重叠群落方面存在困难。与所有这些基线方法相比，本文提出的ComE通过联合建模可以正确地检测出三个类，但对于其他方法，它不能区分聚集在混合社区中的绿色和黄色节点。

5.2 社区检测

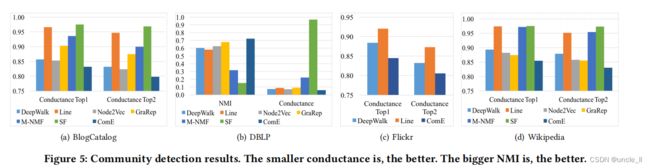
在社区检测中，目标是预测每个节点最有可能的社区分配。作为一项无监督的任务，使用整个图来学习嵌入，从而预测每个节点的社区。请注意，BlogCatalog， Wikipedia和Flickr是多标签数据集，所以我们只计算每个节点的Top2 communities，因为没有明确的方法来计算这种多标签设置的NMI。

在这些实验中，为ComE中的所有数据集设置$\alpha =0.1，\beta =0.1$。如图5所示，ComE在communities和NMI方面始终优于基线。对于communities，ComE在BlogCatalog和Wikipedia上的最佳基线相对提高了2.2%到3.1%，在Flickr上提高了4.4%和3.2%，在DBLP上提高了17.1%。在NMI指标下，ComE实现了6.7%的改善。这些改进表明，建模社区检测和节点嵌入比单独解决它们更好。SF方法的普遍性能较差，也支持了采用闭环模型的假设。此外，还观察到，平均而言，图嵌入方法比其他方法表现得更好，这说明了考虑图嵌入对社区检测的有用性。特别是，Node2Vec恰好是DBLP和BlogCatalog数据集的最佳基线，而GraRep是Wikipedia数据集的最佳基线， 此外根据5.1的观察，M-NMF在建模多标签数据集方面表现不好。

5.3 节点分类

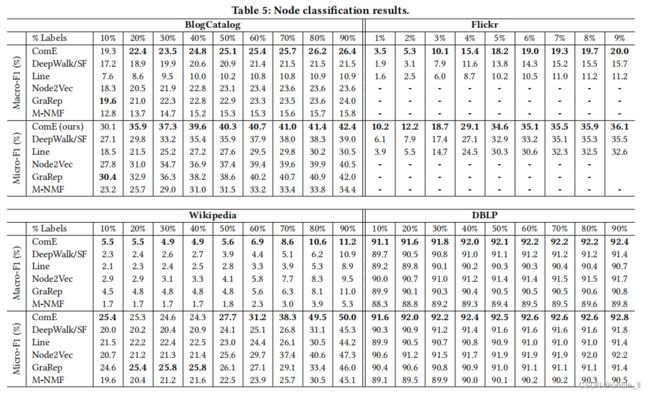
在节点分类中，我们的目标是将每个节点分类为一个或多个类，这取决于它是单标签设置还是多标签设置。遵循[20]，首先训练基于整个图训练图嵌入，然后分别随机分割10%的节点(BlogCatalog、Wikipedia和DBLP)和90%(Flickr)作为测试数据。**使用剩余的节点和它们的标签，通过LibSVM(所有方法的c=1)[6]来训练一个分类器。**重复10次，并报告平均结果。

将ComE与所有基线进行比较。为所有的数据集设置了$\alpha =0.1，\beta =0.01$，除了DBLP，其中保留了$\alpha =0.1和\beta =0.1$。改变训练数据的数量来构建每种方法的分类器。如表5所示，ComE在macro-F1和micro-F1方面都普遍优于基线。特别是，当使用80%(BlogCatalog、Wikipedia和DBLP)，使用8%(Flickr)的标记节点进行训练，ComE将最佳基线相对提高了0.8%至22.6%(macro-F1)和0.71%至48%(micro-F1)。我们的学生t检验表明，上述所有的相对改进在10个数据分割上都是显著的，单尾p值总是小于0.01。有趣的是，ComE改进了节点分类的基线，因为它是无监督的，而且它没有直接优化分类损失。这意味着来自社区嵌入的高阶接近性确实有助于节点嵌入。此外，我们还从表5中做了一些有趣的观察。

首先，在Wikipedia中，当训练中使用少于50%的标记节点时，GraRep的MicroF1分数效果比ComE更好。一个可能的原因是，Wikipedia包含的节点数量比其他数据集要少得多，这导致了一个相对较小的采样路径集。另一方面，GraRep使用转移概率矩阵，它可能比样本路径包含更多的信息，来学习高阶的近似性。这为使用有限的训练标签来训练分类器提供了补充信息。然而，随着更多的标记数据可用，GraRep的这一优势变得更小，ComE开始表现得更好。

其次，可以注意到，在BlogCatalog中，GraRep是最好的基线；同时，Node2Vec在DBLP中优于其他基线。这可能是因为DBLP中的边数比其他数据集的边数要少得多。在平均度较低的图中，Node2Vec学习更容易，这是一个好的邻域。此外，考虑所有其他数据集，**在DBLP中，基于随机游走的方法相对于基于因子分解的方法有效。**这表明，由于随机游走方法的长度和窗口大小的限制，图的平均度会影响性能。除了这种直觉之外，还需要进行更深入的研究来更好地理解随机游动方法的局限性和优势。

第三，在节点分类中，最佳基线与社区检测相反。在第5.2节中， Node2Vec是BlogCatalog和DBLP的最佳基线，而在节点分类任务中，GraRep优于Node2Vec。这表明，关注社区的高阶邻近性比学习形成转移概率矩阵的图结构更有价值，因为在更广泛的任务集中会导致更好的性能。

5.4 模型研究

调整图6中的模型参数α（用于上下文嵌入的权衡参数）和β（用于社区嵌入的权衡参数）。在每个图中，在[0.001, 1] 的范围内调整了一个参数α和β，同时将另一个参数固定为0.1。一般来说，当α和β在[0.001, 1]的范围内时，模型的性能是相当健壮的。具体来说，$\alpha =0.1$为目标函数中的二阶接近性给出了最好的权衡，因为它在Wikipedia和DBLP中提供了最好的社区预测结果，而在BlogCatalog和Flickr中提供了最好的节点分类结果。β的调优不如α那么敏感，特别是在节点分类任务方面。然而，从BlogCatalog中的社区检测性能可以看出，$\beta =0.1$是社区嵌入的最佳权衡。

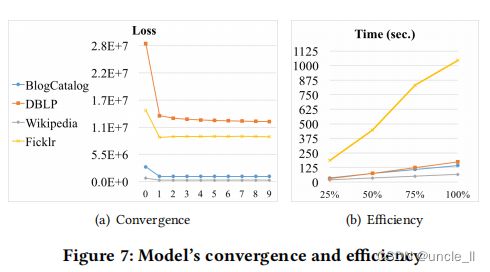
我们进一步验证了图7中ComE的收敛性和效率。记录每次迭代结束时损失函数的值(公式7)来展示所提出的ComE的收敛性。通过|V|对不同数据集的损失值进行规范化，以便更好地在一个图中说明它们。如图7(a)所示，ComE的损失在2-3次迭代内快速收敛。为了证明ComE的效率，在不同尺度的四个数据集上进行了测试。

对于每个数据集，生成三个子集，其中分别保留了边总数和节点总数的25%、50%和75%。注意，为了加快这些实验的计算时间，设置$d=2$和$\zeta =5$。图7(b)显示了ComE算法在不同数据集中的处理时间(第2行-第19行)。显然，ComE的处理时间与图的大小是线性的(即|V|和|E|)，这验证了文章第4部分时的复杂性分析。

6 总结

在本文中，研究一个重要但尚未被充分探索的问题——图嵌入社区，开发了一个建立在社区嵌入、社区检测和节点嵌入之间的闭环。因此，试图共同优化所有这三个任务，以便让它们相互加强。

然后，开发了一个可伸缩的推理算法，它只需要一个复杂的$O(|V|+|E|)$。在多个真实数据集上评估了本文提出的模型，发现我们的模型在社区检测方面的性能提升至少超过6.6%(NMI)和2.2%–16.9%（conductance)），在节点分类方面性能提升至少超过0.8%–26.9%(macro-F1)和0.71%-48%(micro-F1)，它还改进了图形可视化任务中的基线。

参考

• Shiyu Chang andRSM:Dai2016 Wei Han, Jiliang Tang, Guo-Jun Qi, Charu C. Aggarwal, and Thomas S. Huang. 2015. Heterogeneous Network Embedding via Deep Architectures. In KDD. 119–128.
• Mikhail Belkin and Partha Niyogi. 2001. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In NIPS. 585–591.
• Christopher M. Bishop. 2006. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag New York, Inc., NJ, USA.
• HongYun Cai, Vincent W. Zheng, Fanwei Zhu, Kevin Chen-Chuan Chang, and Zi Huang. 2017. From Community Detection to Community Profiling. PVLDB 10, 7 (2017), 817–828.
• Shaosheng Cao, Wei Lu, and Qiongkai Xu. 2015. GraRep: Learning Graph Representations with Global Structural Information. In CIKM. 891–900.
• Chih-Chung Chang and Chih-Jen Lin. 2011. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2, 3 (May 2011), 27:1–27:27.
• Trevor F. Cox and M.A.A. Cox. 2000. Multidimensional Scaling, Second Edition (2ed.). Chapman and Hall/CRC.
• Hanjun Dai, Bo Dai, and Le Song. 2016. Discriminative Embeddings of Latent Variable Models for Structured Data. In ICML. 2702–2711.
• Arther P. Dempster, Nan M. Laird, and Donald B. Rubin. 1977. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 39, 1 (1977), 1–38.
• Hanyin Fang, Fei Wu, Zhou Zhao, Xinyu Duan, Yueting Zhuang, and Martin Ester. 2016. Community-Based Question Answering via Heterogeneous Social Network Learning. In AAAI. 122–128.
• Yuan Fang, Wenqing Lin, Vincent W. Zheng, Min Wu, Kevin Chen-Chuan Chang, and Xiaoli Li. 2016. Semantic proximity search on graphs with metagraph-based learning. In ICDE. 277–288.
• Aditya Grover and Jure Leskovec. 2016. node2vec: Scalable Feature Learning for Networks. In KDD.
• X. He, D. Cai, Y. Shao, H. Bao, and J. Han. 2011. Laplacian Regularized Gaussian Mixture Model for Data Clustering. TKDE 23, 9 (2011), 1406–1418.
• Kyle Kloster and David F. Gleich. 2014. Heat Kernel Based Community Detection. In KDD. 1386–1395.
• Mark Kozdoba and Shie Mannor. 2015. Community Detection via Measure Space Embedding. In NIPS. 2890–2898.
• Zemin Liu, Vincent W. Zheng, Zhou Zhao, Fanwei Zhu, Kevin Chen-Chuan Chang, Minghui Wu, and Jing Ying. 2017. Semantic Proximity Search on Heterogeneous Graph by Proximity Embedding. In AAAI. 154–160.
• Tomas Mikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, and Jeffrey Dean. 2013. Distributed Representations of Words and Phrases and their Compositionality. In NIPS. 3111–3119.
• Mathias Niepert, Mohamed Ahmed, and Konstantin Kutzkov. 2016. Learning Convolutional Neural Networks for Graphs. In ICML. 2014–2023.
• Mingdong Ou, Peng Cui, Jian Pei, Ziwei Zhang, and Wenwu Zhu. 2016. Asymmetric Transitivity Preserving Graph Embedding. In KDD. 1105–1114.
• Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. 2014. DeepWalk: Online Learning of Social Representations. In KDD. 701–710.
• Sam T. Roweis and Lawrence K. Saul. 2000. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 290, 5500 (2000), 2323–2326.
• Mrinmaya Sachan, Avinava Dubey, Shashank Srivastava, Eric P. Xing, and Eduard Hovy. 2014. Spatial Compactness Meets Topical Consistency: Jointly Modeling Links and Content for Community Detection. In WSDM. 503–512.
• Yizhou Sun, Charu C. Aggarwal, and Jiawei Han. 2012. Relation Strength-aware Clustering of Heterogeneous Information Networks with Incomplete Attributes. PVLDB 5, 5 (Jan. 2012), 394–405.
• Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei.2015. LINE: Large-scale Information Network Embedding. In WWW. 1067–1077.
• Lei Tang and Huan Liu. 2011. Leveraging social media networks for classification. Data Min. Knowl. Discov. 23, 3 (2011), 447–478.
• Joshua B. Tenenbaum, Vin de Silva, and John C. Langford. 2000. A Global Geometric Framework for Nonlinear Dimensionality Reduction. Science 290, 5500 (2000), 2319–2323.
• Fei Tian, Bin Gao, Qing Cui, Enhong Chen, and Tie-Yan Liu. 2014. Learning Deep Representations for Graph Clustering. In AAAI. 1293–1299.
• L.J.P. van der Maaten and G.E. Hinton. 2008. Visualizing High-Dimensional Data Using t-SNE. JMLR 9 (2008), 2579–2605.
• Daixin Wang, Peng Cui, and Wenwu Zhu. 2016. Structural Deep Network Embedding. In KDD. 1225–1234.
• Meng Wang, Chaokun Wang, Jeffrey Xu Yu, and Jun Zhang. 2015. Community Detection in Social Networks: An In-depth Benchmarking Study with a Procedure oriented Framework. PVLDB 8, 10 (June 2015), 998–1009.
• Xiao Wang, Peng Cui, Jing Wang, Jian Pei, Wenwu Zhu, and Shiqiang Yang. 2017. Community Preserving Network Embedding. In AAAI. 203–209.
• Jierui Xie, Stephen Kelley, and Boleslaw K. Szymanski. 2013. Overlapping Community Detection in Networks: The State-of-the-art and Comparative Study. ACM CSUR 45, 4 (2013), 43:1–43:35.
• Ruobing Xie, Zhiyuan Liu, Jia Jia, Huanbo Luan, and Maosong Sun. 2016. Representation Learning of Knowledge Graphs with Entity Descriptions. In AAAI. 2659–2665.
• Liang Yang, Xiaochun Cao, Dongxiao He, Chuan Wang, Xiao Wang, and Weixiong Zhang. 2016. Modularity Based Community Detection with Deep Learning. In IJCAI. 2252–2258.
• Wayne W. Zachary. 1977. An Information Flow Model for Conflict and Fission in Small Groups. Journal of Anthropological Research 33, 4 (1977), 452–473.

参考

• https://zhuanlan.zhihu.com/p/36924789
• https://flashgene.com/archives/34850.html