论文阅读Reliable Traffic Monitoring Mechanisms Based on Blockchain in Vehicular Networks

摘要

实时的交通流监测是智慧城市中交通条件和预防危险事的建设基础。本文提出了一个可信和高效的交通流检测系统并整合了区块链和车联网的强势技术。它可以将其交通信息收集任务众包给在路上行驶的车辆，而不是在每个角落安装摄像头。首先，我们设计了一个轻量级的基于区块链的信息交易框架去模拟交通管理部门和车辆的交互；其次，我们定义了系统中的实体的基本功能，考虑到增加预算的机制即汽车主动接收收集的任务。在我们的算法中，不只保证对所选车辆的总付款不超过给定的预算，而且还保持拍卖过程的真实性，避免某些车辆提供不真实的出价以获得更大的利益。最后，我们搭建了实验去评价基于所提出的算法对数据交易框架和性能，结果证明正确性和效率兼顾。

介绍

在过去的几年里，随着技术的进步，车辆通过安装摄像头传感器、微型计算机和通信设备变得越来越智能 。这些车辆与自身和其他设施相连，形成车辆网络。由于其潜在的商业价值，车联网（IoV）已成为学术界和工业界关注的热门话题。车联网为用户之间的交通事故、路况等信息交换和共享提供了一个便捷的平台，可以有效提高资源的利用率和交通状况。然而，车载网络中涉及的移动和可变实体太多，它们通常是陌生人，彼此不信任。正因为如此，车联网中的信息交换仍然面临着如何在实际应用中确保信息安全和隐私保护的巨大挑战。
区块链技术的出现使得改变这一切成为可能。区块链是自 2008 年中本聪发表白皮书以来进入人们视野的公共分布式数据库。区块链利用现代密码学知识和分布式共识协议来达到安全和隐私保护的目的。在这里，数字签名是实现身份认证和避免信息泄露的有效手段，而共识协议允许信息在互不信任的用户之间自由交互，无需第三方平台。因此，由于它的去中心化、安全性和匿名性，它可以用来构建一个可靠的信息交易系统。尽管如此，如何基于车联网设计合理的区块链结构，提高信息交换效率，保证定价策略的真实性，仍然是一个值得深入探讨的问题。
在本文中，我们考虑这样一个场景：在智慧城市中，有一个**交通管理局（TA）**负责通过收集该城市各个道路节点的信息来监控实时交通状况。传统的做法是在各个道路节点安装摄像头，但这样做成本高且容易受到自然和人类活动的破坏。尤其是在一些偏远的角落，不需要单独安装摄像头。在 IoV 的驱动下，TA 可以将其交通信息收集任务众包给在路上行驶的车辆。在这个情况下，研究智能城市中的交通管理TA与车辆之间的交通信息交换，存在如下两个挑战：
（1）如何构建一个可靠、高效的区块链实现的交通信息交易框架？
（2）如何建立公平、真实的机制，选择一部分车辆作为信息提供者，以最大限度地提高 TA 的利益，同时防止恶性竞争？

为了应对第一个挑战，我们提出了一个基于区块链的实时交通流量监测(BRTM)的系统，在TA和车辆之间达成一种可信和高效的信息交易处理。首先，我们使用现代加密方法和数字签名技术去保护通信内容不发生隐私泄露。传统的POW共识机制算力耗费极高、验证速度较慢，因此不能应用在汽车网络这种资源受限的环境。因此，我们设计了轻量级区块链依赖基于声誉的DPoS的共识机制，能够减少验证的时间，并改进系统的吞吐量。在这里，可以将不同城市的所有 TA 视为全节点，它们相互连接以完成共识过程。 BRTM 系统中的每个 TA 都有一个与 TA 相关联的声誉值，这反映了它在之前的共识轮次中的行为。 具有较高声誉值的全节点意味着它具有较高的投票权重，并且更有可能成为未来共识轮的领导者，从而保证共识过程的可靠性和效率。

对于第二个挑战，我们提出了一种预算拍卖机制，以激励城市中的车辆积极承担 TA 下达的任务。TA 发布了一个任务集，其中包含许多关于不同位置的交通信息的不同任务。本市每辆现役车辆向 TA 提交其可以完成的任务和相应的投标，然后 TA 从这些现役车辆中选出一组优胜者来承担其任务并支付相应费用。我们的目标是通过选择最佳获胜者集来最大化 TA 的利润，这可以归类为具有背包约束的非单调子模最大化问题。简单的贪心策略可以给我们一个有效的解决方案，但它不满足真实性。如果不真实，车辆可能会通过提高报价或与其他车辆串通来增加其效用，这将损害拍卖机制的公平性和有效性。因此，我们设计了一种真实预算选择和定价（TBSAP）算法，可以保证预算拍卖机制的个体合理性、盈利性、真实性和计算效率。

最后，通过数值模拟评估了我们提出的机制的有效性。 结果表明，我们提出的机制可以通过敦促节点正确行事并确保信息交易的公平和真实来提高区块链系统的可靠性。 据我们所知，这是第一次在车辆网络中提出可靠的基于区块链的交通监控系统，该系统基于预算拍卖机制以实现利润最大化。 本文的其余部分组织如下：第二节我们讨论目前有的先进工作；第三节介绍BRTM交通监控系统并定义功能；第四节介绍了轻量级区块链设计；第五节提出了一个真实的预算拍卖机制；第六节中通过数值模拟评估我们提出的系统和算法，并在第七节中展示结论。

相关工作

随着物联网（IoT）的发展，车辆不再是孤立的个体，而是连接网络中的节点，这导致了车联网的形成。随后，由于计算能力和现代通信设备的进步，车联网得到了进一步的发展。Kaiwartya等人提供了一个主要关注网络架构的 IoV 框架；Singh提出了 IoV 的抽象网络模型，并与依赖于流行技术的不同服务相关；Ji为未来的 IoV 设计了一种新颖的网络结构，并对基本的 IoV 信息进行了全面回顾，其中包括几种网络架构和 IoV 的代表性应用。
近年来，区块链技术的兴起颠覆了传统物联网的运行模式，基于区块链的物联网推动了交易方式的变革。首先，在能源交易方面，Li 等人为依赖联盟链和基于信用的支付方案的工业物联网设计了一个安全的能源交易区块链系统；Guo提出了一种基于区块链的分布式多能源交易框架来解决安全和隐私保护问题；Xia提出了一种支持区块链的车对车电力交易方案，该方案利用贝叶斯博弈定价来处理不完整的信息共享。其次，在计算资源交易方面，Yao研究了云服务器和矿工之间的资源管理问题，因为工业物联网的计算能力有限。Ding为区块链平台创建了一种机制，以吸引轻量级设备从边缘服务器购买更多计算能力以参与挖矿。最后，在信息交易中，Wang通过结合区块链、网络模型和共识算法，设计并实现了一个更安全、更可靠的政府信息共享系统；Xu设计了一个基于区块链的大数据共享框架，适用于资源有限的设备。Chen提出了一种基于区块链的数据交易框架，该框架依托联盟区块链实现车联网安全、真实的数据交易。然而以上工作并没有真正实现可靠性，并且忽略了共识过程的高延迟。
在本文中，我们的交易模型与之前的任何一种都不同，并试图仔细设计一个安全可靠的系统。拍卖机制作为一种博弈论技术，已被用于解决各种应用中的分配和定价问题，例如移动众筹、边缘计算和频谱交易。Zhang调查了鼓励用户参与移动众包的各种激励策略；Yang分别在Stackelberg博弈和反向拍卖理论的框架下设计了两个众包模型。 Kaini提出并解决了层次模型背景下的基于拍卖的利润最大化问题。Jiao提出了一种基于拍卖的市场模型，用于计算边缘服务器和矿工之间的资源分配。Zhu为无线电网络中的协作感知设计了一种真实的双重拍卖机制。Zheng通过重新分配无线信道实现了社会福利最大化问题，同时他们也考虑了策略证明。在本文中，我们提出的拍卖机制类似于移动众包下的拍卖机制，但我们的模型中有一个预算约束来限制获胜者集的范围。因此，无论是理论分析还是适用范围都不同于以往的工作。

交通监测系统

第三节，我们的交通监测系统包含实体的网络模型和基本功能。

A 网络模型

我们以图 1 为例进行演示，如图 1 上半部分所示，达拉斯市有一个 TA，宣布了全市重要路口的多项交通信息采集任务。这个城市的一些车辆要求以一定的价格承担部分任务。对于车辆而言，其请求能否被接受由TA根据TA的评估决定。然后，在美国建立了一个BRTM系统，如图1下部所示。洛杉矶、芝加哥、纽约和达拉斯这四个主要城市相互连接，形成一个大网络。

考虑到智慧城市的发展需要，城市中的交通管理(TA)有责任实时监测交通状况，可以通过众包将他收集交通信息的任务通过支付一定费用的方式给到在行驶的汽车。因此，基于区块链的实时交通监控系统BRTM包括两个重要实体：TA和车，如上图所示。在BRTM系统中，智慧城市 Sa 中实体的功能，a ∈ Z+，可以表示如下：
Traffic administration (TA):城市 Sa 的 TA 可以用 T Aa 表示，它收集了在这个城市运行的车辆的实时交通信息。例如，在高峰时段，一些交通繁忙的道路上经常发生交通事故。这时，T Aa 需要根据那些在指定位置行驶的车辆提供的响应，即时分析路况。如果 T Aa 采用某些车辆提供的信息，它必须向它们支付数据币。在这里，数据币是一种数字货币，被视为交通信息的支付方式。
车辆：本系统中的车辆安装有摄像头传感器、无线通信设备和微机系统，能够对数据进行采集、处理，并将数据传输到其他相应的设备。城市 Sa 的活跃车辆可以表示为一组 Va = {va1, va2,···,vab,···}，其中活跃车辆是与 T Aa 参与信息交易的车辆，闲置车辆不想参与分享他们的交通信息。一旦 T Aa 和 vab 之间的交易完成并验证，车辆 vab 将从 T Aa 收到一定数量的数据币。
基于此，我们的BRTM系统中的智慧城市可以表示为Sa = (T Aa, Va)，整个BRTM系统S可以表示为S = {S1, S2,···,Sa,··· }。很容易理解，比如这个系统可以建在一个由多个智慧城市组成的国家，在这里，服务于 S 城市下的所有 TA 都相互连接，组成一个点对点 (P2P) 广域网。
BRTM系统中TA之间的P2P网络用于构建区块链网络。 在这里，区块链是记录交易和保证安全的有效技术。 在我们的区块链网络中，有两种类型的节点，即全节点和轻量级节点。 对于全节点，他们不仅执行共识过程来验证候选块，而且还管理包含 TA 和车辆之间的整个交易的区块链， 对于轻量级节点来说，它们只存储方便它们检查和验证的块头。 在我们的系统 S 中，由于缺乏足够的存储和计算能力，Sa ∈ S 的每个 T Aa 都默认为全节点，而 Sa ∈ S 的每个车辆 vab ∈ Va 都默认为轻量级节点。

B 基本功能的定义

考虑一个智慧城市 S = (T A, V ) 使得 S ∈ S 在某个点上，我们忽略下标并表示为 V = {v1, v2, · · · , vn} 为方便起见。

这个交通管理部门TA发布了一个关于交通信息的任务集T = {t1, t2, ···, tm}，供活动车辆承担。对于 T A，每个任务 tj ∈ T 都有一个评估 aj。对于每个车辆 vi ∈ V ，它可以根据其能力和意愿尝试完成任务子集 Ti ⊆ T。汽车的任务成本即 vi 的 Ti 成本可以定义为 ci，它是私有的，TA 不知道。然后，车辆 vi 确定一个投标 bi 并用它的投标任务对 (Ti, bi) 响应 T A，其中bi 是 vi 的底价，即它要承担任务 Ti 的最低价格。一般来说，对于任何车辆 vi 和 vj，我们有 Ti ∩ Tj 不等于 ∅。在这里，对于每个任务 ti ∈ T，我们可以将其量化为该城市某个位置的交通信息，从而主动车辆能够根据其运行路径提交任务子集。在收到所有活跃车辆的响应后，TA 需要选择一个获胜者（接受）集合 W ⊆ V 并为每个 vi ∈ W 给出一个支付 pi。
车辆 vi ∈ V 的效用和T A的收益如下所示，其中我们表示A(W)如下。此外，为了控制成本，T A有一个总的预算值B。因此我们要设计对应的激励机制去进行拍卖程序。

轻量级区块链设计

在智慧城市中，TA首先发布一个任务集，然后该城市中的那些活跃车辆请求承担部分任务。 如果车辆的请求被 TA 接受，它将获得一定数量的奖励。 借助区块链技术，TA可以以去中心化、安全、可验证的方式与主动车辆进行交通信息交易。 同时，预算拍卖机制写入智能合约。 当新一轮交易开始时，我们的 BRTM 系统中的智能合约将自动部署和执行，以便根据车辆的请求为 T A 找到最佳利润。

系统初始化

智慧城市S=（TA,V)，每辆车 vi ∈ V 必须通过关联其车牌向证书颁发机构 (CA) 注册，以获得唯一的标识 IDi。然后，每个合法车辆将被分配一个私钥/公钥对（SKi，P Ki），其中私钥是自己保留的，公钥被区块链中的所有合法节点称为假名。为了数据的完整性，目前的区块链技术广泛采用非对称加密。由private（resp.public）密钥加密的数据可以由public（resp.private）密钥解密。注册后，车辆vi将获得一份由CA的私钥签名的证书Ceri，可以证明其身份的真实性。有一个账户 Ai = {IDi, Ceri, (SKi, P Ki), Bi} 与 vi ∈ V 相关，其中 Bi 是其数据币余额。同理，T A 也有一个账户，记为 A∗ = {ID′, Cer′, (SK′, P K′), B′, Rep′}，其中 Rep′ 是它的信誉值，后面会介绍。如果一轮交易成功完成，数据币将从 B∗ 转移到 Bi。

信息交易框架

交通信息交易在BRTM系统的步骤如图：

1. T A 在该城市的活跃车辆上发布其任务集 T。发布的消息可以表示为 PubMsg = {SK′(T ), Cer′, STime}，其中为安全起见，任务集由 T A 的私钥加密，STime 是该消息的时间戳一代。
2. 在收到 T A 的 PubMsg 后，该城市中的每辆现役车辆 vi ∈ V 必须通过 CA 的公钥验证 T A 的认证 Cer′，然后读取 T A 的公钥设置的任务。一旦通过验证，每个 vi 将确定其任务-投标对 (Ti, bi) 并将其请求消息 ReqMsg（记为 ReqMsg = {P K′(Ti, bi), Ceri, ST ime}）发送回 T A . 这里，它的任务-投标对是由TA的公钥加密的，因为它只能被TA读取以保护隐私。
3. T A 等待从该城市的活跃车辆中收集所有的 ReqM sg，然后确定获胜者集合 W 及其对应的 vi ∈ W 的支付 pi。此过程由内置智能合约执行，该合约采用第 2 节中解释的预算拍卖机制。
4. T A 向每个接受的车辆 vi ∈ W 发送订单消息，可以表示为 OrdMsg = {P Ki(pi), Cer’, STime}。在这里，支付是由 vi 的公钥加密的，vi 只能读取该公钥。
   5）如果收到来自TA的OrdMsg，说明vi已经被选为信息提供者。然后，vi 可以通过其私钥读取它，并将包含与任务 Ti 相关的流量信息的响应消息发送回 T A。由于与（2）相同的原因，数据被 T A 的公钥加密。
5. 数据传输完成后，TA会检查并确认来自vi的任务Ti的流量信息是否满足其要求。如果是，TA 将数据币 pi 支付给 vi 的公共钱包地址。
6. 一旦收到TA的付款，vi会向TA发送确认消息，记为ConMsg = {P K′(Confirm), Ceri, STime}，TA会用a签名确认消息，然后形成一个交易记录到现在。
7. T A 内置的智能合约会记录一段时间内 T A 与本市车辆之间的一系列交易，并将其打包成一个新的区块。在将该区块加入区块链之前，必须在 BRTM 系统中的所有 TA 之间达成共识。我们在这里采用的共识过程称为基于信誉的委托工作证明 (DPoS) 机制，在接下来进行了解释。完成共识机制，该区块将按照线性和时间顺序永远上链。

基于声誉的DPoS机制

在区块链系统中共识的处理对于一致性和安全性的保证是至关重要的。经典PoW共识机制因为算力的限制不适合本系统，因此我们设计了一种新的基于声誉的DPoS机制，既可信又能提升性能。如之前说的TA们在BRTM这个系统中 S 是作为全节点，因此共识步骤在这些节点之间进行。步骤如下
1）选择见证人：用全节点集合Z = {T A1, T A2,····,T Aa,····}表示，每个全节点T Aa ∈ Z都有一个信誉值Repa。这个信誉Repa可以被视为直接决定其投票权重的权益。 这意味着具有较高信誉值的节点可以比具有较低信誉值的节点更多地确定结果。 在每个见证人选举时期，每个 T Aa ∈ Z 的投票结果 Ra 定义为

其中I(a, a′)是一个指标，如果这个指标=1说明T Aa′支持T Aa，如果=0则不支持。所有声誉值和投票结果都会被存在链上，因此每个节点都可以检查。我们选了一个见证人委员会M ⊆ Z即有最高的投票结果|M|。然后，它可以分为两部分，即 M = D ∪ E 和 D ∩ E = ∅，其中 D 中的全节点是活动见证人，E 中的全节点是备用见证人。 活跃的见证人有 |D| 最高投票结果，能够像领导者一样生成新区块。 但是，备用见证人只能验证和广播由活动见证人生成的块。
2）生成区块：首先，集合 D 中的活跃见证者按随机顺序排序。 然后，每个 T Aa ∈ D 根据这种排序轮流成为领导者，负责生成新的块。 领导者必须验证和检查最近发生的所有交易，并将这些有效交易打包到一个新块中。 如果一个节点在给定的时间内没有成功出块，它将被跳过并且在这个选举时期没有机会再次成为领导者。 通过|D| 共识轮次之后，即一个选举时期，我们重新执行见证人选举，根据 Z 中全节点的新声誉值选举新的见证人委员会 M。
3）共识过程：当生成新区块之后，领导节点会广播给所有M的见证人。所有见证人会验证领导的身份并检查区块，然后广播他们的验证结果并通过他们的私钥签名。接下来，每个见证人 T Aa ∈ M 将其验证结果与其他见证人的结果进行比较。 如果确认，它将向领导者发送确认消息，这意味着该见证人同意接受新块。 对于领导者来说，如果同意接受这个区块的见证人比例超过三分之二，它就会将新区块附加到区块链中。 所有全节点应根据最长链原则同步其本地区块链存储，所有轻量级节点应根据最新的区块链头更新。
4）更新声誉值：当共识回合完成或者被终端之后，我们需要根据节点在共识过程中的表现更新Z的全节点的声誉值。通常来说，积极行为会积累声誉值，而恶意行为会有不好的影响。Repa(i)表示属于T Aa ∈ Z节点的声誉值在i-th个共识回合后。在i-th轮共识回合，我们对T Aa ∈ Z的每个全节点定义了

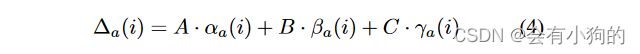
此处，如果 T Aa ∈ Z 参与了见证人选举的投票，我们给出 αa(i) = 1，否则 αa(i) = -1。 当 T Aa 是本轮共识的领导者时，如果它生成一个最终被其他见证人接受的新块，我们给出 βa(i) = 1，否则 βa(i) = -1。 如果 T Aa ∈ Z{leader} 不是领导者，我们给出 βa(i) = 0。当 T Aa ∈ M{leader} 是见证委员会成员但不是领导者时，我们给出 γa(i ) = 1，如果它正确验证了领导者生成的块，否则 γa(i) = -1。 如果 T Aa ∈ Z\M 不是见证人，我们给出 γa(i) = 0。那么，A、B 和 C 是三个可调节的参数，分别代表投票、领导和验证行为的奖励或惩罚。 基于其在第 i 轮共识中的行为 Δa(i)，我们将全节点 T Aa ∈ Z 的信誉值定义为

根据（3），当 T Aa 的声誉降至零时，T Aa 的投票毫无意义。 此外，我们为每个 T Aa ∈ Z 初始化信誉 Repa(0) = 0.5，并因为它们的重要性而使 B > C > A > 0。

可信度和性能

我们的BRTM系统继承了区块链技术的优势，有助于确保交通信息交易的可靠性和隐私保护。其主要特点概括如下： （1）去中心化：交通信息交易可以分布式进行，不依赖第三方可信中介，避免单点故障； （2）可靠性：当有节点因恶意攻击而失效时，可以保证区块链网络正常工作； (3) 隐私保护：非对称加密用于防止消息被他人阅读，使私人消息在拍卖过程中保持机密； （4）效率：我们基于信誉的DPos机制不仅使共识过程更加可靠，而且通过提前筛选出可信节点来提高效率； (5) 交易认证：所有交易在附加到区块链之前必须经过见证人的检查和验证，因此很难控制大多数见证人来创建一个虚幻区块。基于此，我们的BRTM系统为我们提供了一个安全、可靠、高效的交通信息交易平台。

预算拍卖激励机制

本章我们思考如何对S = (T A, V )的TA 和vi ∈ V的交易过程进行建模。拍卖机制在其中是一个优秀的理论工具，此处卖家为V = {v1, v2, · · · , vn}，买家是 TA。每个卖家vi 提交任务-投标额度，即(Ti, bi)，然后买方决定是否接受其请求。 如果接受，买方需要提供付款。 我们将这种拍卖称为“反向拍卖”。 因此，单轮拍卖机制可以表述为问题 1。

问题1

S 中的活跃车辆给定任务-投标对向量 ((T1, b1), (T2, b2), · · · , (Tn, bn))，TA 需要计算分配 W 和支付 {pi}vi ∈W 使得

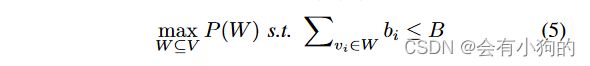
这个等式满足个人理性、盈利能力、真实性和计算效率。 我们在本节中使用的拍卖是单一的密封投标拍卖，因此每个卖家给出的任务投标对是私人的，其他卖家不知道，以避免合作或结成联盟。 一旦提交，任何卖家都不能在拍卖期间更改其任务或出价， 这就是我们在 Sec 中使用非对称加密的原因。

定义1（个人理性）

如果没有获胜的卖家获得低于其成本的价格，则反向拍卖是个人理性的。
对于每个车辆 vj ∈ V ，如果 vi ∈ W ，它必须具有 pi ≥ ci 的非负效用。

定义 2（盈利能力）

反向拍卖的利润是获胜者集合产生的价值与向卖家支付的款项之间的差额，它是非负的。
对于S中的TA，对应的分配W符合

定义3（真实性)

如果每个卖方的出价与其真实成本相同，则反向拍卖是真实的，是最大化其效用的主导策略。
对于每个车辆 vi ∈ V ，这意味着无论其他人的出价是什么，vi 都无法通过给出与其真实成本 ci 不同的出价 bi 来增加其效用。真实性是拍卖机制避免恶意价格操纵以及确保公平良性的市场竞争环境的一个非常重要的属性。在我们的案例中，如果车辆在提供不真实的出价时可以获得更好的效用，那么那些恶意车辆就能够在拍卖中作弊，使自己受益，但损害他人的利益。通过让所有现役车辆如实出价，TA 可以将其任务分配给最合适的车辆。因此，真实性在我们的拍卖设计中起着非常重要的作用。

定义 4（计算效率）

如果反向拍卖可以在多项式时间内完成，则它是有效的。

A 子模块最大化

假设 T A 为每辆车 vi ∈ V 给出一个支付 pi当pi = bi，问题 1 可以简化为一个优化问题，称为“预算车辆分配问题”，它选择一个获胜者集 W⊆ V 使得 P ̄ (W ) 被最大化。 我们表示

其中∑ vi∈W bi ≤ B。为了有意义，我们假设 ̄ P (∅) = 0 并且存在至少一辆车辆 vk ∈ V 使得 ̄ P ({vk}) > 0 且 bk ≤ B。但是，预算车辆分配问题可以简化为 多项式时间内的经典集合覆盖问题，因此很难确定找到最优解。 基于此，我们必须寻求帮助，设计一种近似算法，该算法将利用 (6) 中所示的目标的子模性。

定义 5（子模块函数 ）

给定一个集合函数 f : 2V → R，如果子模块

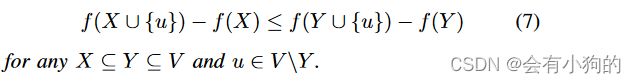
引理 1 ： 预算车辆分配问题 ̄ P 的目标函数是次模的。

众所周知，Buchbinder 等人为无约束的子模最大化问题设计了一种双贪心算法，在确定性设置下具有（1/3）近似值，在随机设置下具有（1/2）近似值。回到我们的预算车辆分配问题，有一个约束 ∑vi∈W bi ≤ B，它是一个背包约束。此约束影响 T A 获得的最终利润以及在拍卖中被选为获胜者的车辆数量。因此，需要一个有效的反向拍卖机制设计来仔细确保真实性。基于上述分析，该优化问题可以归类为具有背包约束的非单调子模最大化问题。李等人。 [28] 提出了一种 (1/5 - ) 逼近算法，通过分数松弛和局部搜索方法最大化任何具有背包约束的非负子模函数。尽管该算法可以给我们一个恒定的近似比，但它的过程很复杂，而且它的性能实际上比贪心启发式算法差。贪心启发式算法如算法 1 所示。

在这里，我们用 ̄ P (vi|W ) = ̄ P (W ∪ {vi}) − ̄ P (W ) 表示，b∗ 是车辆 v∗ 的出价。如算法 1 所示，我们从当前约束集 F 中选择具有最大单位边际增益的车辆 v∗ 直到 ̄ P (v∗|W ) < 0 或 F = ∅。尽管算法1返回的获胜者集由于非单调性和背包约束而没有任何理论界限，但它直观且在实际应用中具有良好的性能。现在，我们必须探索贪婪启发式是否满足上述反向拍卖机制中的四个属性。接下来，让我们看看贪心启发式是否满足盈利能力、个体理性、真实性和计算效率如下：
1）个体理性：T A 支付每辆车的中标者出价，因此它是个体理性的
2) 盈利能力：形成算法 1 中的第 5 行，当没有车辆具有正边际收益时终止 while 循环，这保证了 ̄ P (W ) > 0。
3) 真实性：让我们考虑一个例子。 T A 发出五个任务，记为 T = {t1, t2, t3, t4, t5}，评价为 {a1 = 2, a2 = 3, a3 = 4, a4 = 2, a5 = 5}，预算 B = 5。
这个城市有三辆现役车辆，用 V = {v1, v2, v3} 表示。他们想要承担 T A 的任务 T1 = {t1, t3, t5}, T2 = {t1, t2, t5}, T3 = {t3, t4, t5}, c1 = 2, c2 = 2, and c3 = 2. 当每辆车如实出价时，我们有 ̄ P ({v1}|∅)/b1 = (A({v1}) - b1)/b1 = (11 - 2)/2 = 4.5。同样，我们有 ̄ P ({v2}|∅)/b2 = 4 和 ̄ P ({v3}|∅)/b3 = 3.5。因此，车辆 v1 在第一次迭代中被选中。在第二次迭代中，我们有 ̄ P (v2|{v1})/b2 = 0.5 和 ̄ P (v3|{v1})/b3 = 0。因此，在第二次迭代中选择了车辆 v2。然后，由于预算用尽，贪心启发式终止。然而，当车辆 v2 提供不真实的出价 b2 = c2 + λ 时，我们有 ̄ P (v2|{v1})/b2 = 3/(2+λ)−1。如果 λ ∈ (0, 1)，它将在第二次迭代中被选为获胜者。算法在此终止，车辆 v2 可以通过提供不真实的出价获得更多的付款，因此不满足真实性。 4）计算效率：贪心启发式的运行时间为O(Bnm/ minvi∈V {bi})，因为它需要O(nm)，|T | = m 和 |V | = n，计算 ̄ P 并且最多迭代 B/ minvi∈V {bi} 次，因此计算效率很高。

B真实拍卖机制设计

如上所述，贪心启发式算法由于缺乏真实性而没有意义，即使它易于实现。因此，我们必须设计一种预算反向拍卖机制，不仅通过鼓励车辆承担任务获得良好的利润，而且满足如前所示的四个属性，特别是真实性，以防止恶意操纵这个系统提供不真实的出价。因此，需要设计一个有效的拍卖机制，尽管它可能会损失一些利润。我们基于 Myerson 的介绍 提出了一种真实的预算逆向拍卖机制。
定理 1：一个反向拍卖机制是真实的当且仅当它满足如下条件： (1) 单调性：如果车辆（卖方）vi ∈ V 以它的任务-投标对 (Ti, bi) 获胜，那么它将以任何满足以下条件的投标获胜在相同的任务集 Ti 下也比 bi 小。即，当其他卖家不改变策略时，(Ti, b◦ i ) 将以任何出价 b◦ i < bi 获胜； (2) 关键支付：获胜者 vi 及其任务-投标对 (Ti, bi) 的支付 pi 是 vi 可以获胜的最高投标。也就是说，当其他卖家不改变他们的策略时，(Ti, b◦ i ) 不会以任何出价 b◦ i > pi 获胜。

仿真

在这个部分，我们首次评估了这个机制的性能，然后测试我们的预算反向拍卖算法的正确性和效率。将显示模拟设置和结果。

A. 模拟设置

为了评估基于信誉的 DPoS 机制，我们需要观察共识轮中的不同行为如何影响其信誉值。这里我们以两个全节点为例进行演示，一个是正常节点，行为合法，另一个是异常节点，有时会做出一些错误行为，例如在见证人选举中不投票，产生无效块为领导者，或错误地验证区块。如（4）所示，我们给出参数 A = 0.005，B = 0.05，和 C = 0.01。然后，我们将我们基于信誉的 DPoS 与一般 DPoS 机制进行比较，后者 Z 中的每个完整节点都由相同的投票权重给出。换句话说，我们在一般 DPoS 的见证人选举中不考虑他们的声誉值。

在这两种 DPoS 机制中，每个正常的全节点 T Aa 投票支持 T Aa′ ∈ Z{T Aa} 且 Repa′ ≥ θ 其中 θ = 0.5 是一个阈值。相反，我们考虑最极端的情况，即每个异常全节点 T Aa 投票支持 T Aa′ ∈ Z{T Aa} 且 Repa′ < θ。在我们的 BRTM 系统中，我们用 |Z| 定义完整的节点集。 = 100和图3。信誉值随着共识过程中两个全节点的不同行为而变化。图 4 正常见证人（RNW）的比例随着异常全节点（RAFN）的比例变化。证人委员会与 |M| = 70。

为了模拟真实状态，我们通过从 [0.5, 1] 均匀采样来给出正常完整节点的信誉值，通过从 [0, 0.5) 均匀采样来给出异常完整节点的信誉值。为了评估该系统的可靠性，我们将异常全节点（RAFN）的比率定义为“[#异常全节点]/|Z|”正常见证人的比率 (RNW) 为 [# normal witnesses/M]。为了模拟预算反向拍卖机制，我们考虑一个面积为 1000m × 1000m 的智慧城市 S = (T A, V )，并且 T A 发布的任务集 T 分布在该区域上。然后，现役车辆V也任意分布在该区域上。对于每辆车 vi ∈ V ，它的检测能力是不同的，因此我们假设有一个检测距离 di 均匀分布在 [10, 30] 中。这意味着 vi 的任务集 Ti 包含了与 vi 的距离小于 di 的所有任务。最后，TA 对每个任务 tj ∈ T 的评价 aj 均匀分布在 (0, 10] 中，并且 vi 的 Ti 成本可以表示为 ci = κ · |Ti| 其中参数 κ 分布在 (0, 5] 统一

B. 仿真结果与分析

我们的基于信誉的 DPoS 机制的仿真结果如图 3 和图 4 所示。

1. 行为对信誉的影响：图 3 描绘了信誉值随不同程度的变化两人的行为全节点共识过程。如图 3 所示，我们可以看到正常节点的声誉因其合法行为而逐渐增加，但异常节点的声誉因其错误行为而降低。在这里，我们假设每个选举时期有 10 轮共识，即 |D| = 10。对于普通节点，它在第一个选举时期（第 1 到第 10 轮）投票选举见证人，每轮增加 0.005 声望。在第二个纪元（第 11 轮到第 20 轮），由于其良好的声誉，它被选为见证成员。因此，它正确地投票和验证区块，每轮增加 0.015 声誉。特别是在第 15 轮共识中，它成为成功出块的领导者，在本轮中增加了 0.055 的声誉。这些合法行为增加了它的声誉，直到接近 1。对于异常节点，它在第三个 epoch（第 21 到第 30 轮）被选为见证成员。它不会对区块进行投票和验证，这会降低每轮 0.015 的声誉。特别是在第 15 轮共识中，它成为成功出块的领导者，在本轮中增加了 0.055 的声誉。特别是在第 25 轮共识中，它成为生成无效区块的领导者，这在本轮中降低了 0.055 的声誉。

2. 可靠性：图 4 画出了正常见证人的比例随着异常全节点比例的变化，描述了我们的 BRTM 系统的可靠性。正常见证人的比例越高，这个系统就越可靠。如图 4 所示，理想线是我们理论上可以得到的最大 RNW。例如，如果 RAFN 为 0.6，即有 60 个异常全节点，则最优 RNW 等于 100·(1-0.6)/70。当 RAFN 小于 0.5 时，RNW 均接近理想值。这是因为异常节点的数量少于正常节点，因此它们的投票几乎不会改变见证人选举的结果。然而，当 RAFN 从 0.5 到 0.75 时，我们的基于信誉的 DPoS 的 RNW 明显大于一般 DPoS 的 RNW，因为普通节点的投票权重较大，尽管它们的数量总体上很小。因此，我们系统的可靠性通过基于信誉的 DPoS 得到提高，尤其是当异常节点的比例较高时，最极端的情况是每个异常节点都投票支持所有异常节点。我们的预算反向拍卖机制的仿真结果如图 5 和图 6 所示。

3. TA 的利润函数：图 5 绘制了不同预算和车辆数量下贪婪启发式和 TBSAP 算法获得的性能这个城市，那里的车辆数量|V |是 500 或 1000。如图 5 所示，我们可以观察到，在任何预算下，TBSAP 获得的 TA 的利润都小于贪婪启发式获得的利润，以确保真实性。对于贪心启发式得到的结果，我们可以观察到 TA 的利润随着预算的增加而增加。当预算大于 200 时，TA 的利润保持不变。 TBSAP 得到的结果也有类似的演变趋势，但在预算大于 200 时略有下降。此时可选车辆都没有正的单位边际增益，因此算法第 25 行的操作步骤2 有可能增加支付并进一步减少利润。

4）投标和付款：图6绘制了预算B = 100的不同车辆数量下每辆车的投标和付款分布。如图6所示，我们可以看到点更集中在底部当车辆数量较多时，剩下的投标和付款较低。这是因为可以选择出价较低的活跃车辆更多来承担收集任务。它解释了为什么 TA 的利润随着这个城市的车辆数量而增加。

结论

在本文中，我们设计并实现了一个基于区块链技术和预算反向拍卖机制的可靠高效的流量监控系统。 为了提高系统的安全性和可靠性，我们给出了一个使用非对称加密的轻量级信息交易框架。 我们设计了基于信誉的DPoS共识机制，以提高区块链记录和存储的效率。 然后，为了激励车辆承担收集任务，我们开发了一种满足个人理性、盈利能力、真实性和计算效率的预算逆向拍卖算法。 最后，数值模拟结果表明我们的模型是有效的，验证了我们算法的正确性和有效性。