数字信号处理二：离散时间信号的运算
一、离散时间信号的基本运算
离散信号的基本运算包括：（1）自变量的变换：平移、反转；（2）两个信号之间的运算：相加、相乘；（3）信号自身整体的运算：信号在值域上的展缩和上下平移，即x(n) ->y(n) = ax(n) + b，a、b 均为实数。离散信号一般不做自变量上的尺度变换。
1、序列的自变量的变换
信号自变量的变换一定要深刻理解“一切变换都是针对时间变量 n 而言的”这句话。
（1）序列的平移
序列的平移是指 x(n)->x(n0 +n) ，将 x(n) 向左或向右平移 n0 个单位。
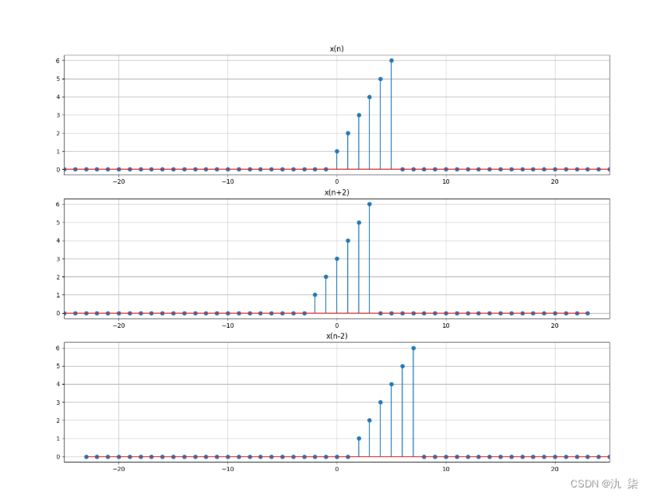
【例 2-1】已知 x(n) = {1,2,3,4,5,6}，分别画出 x(n) 、 x(n + 2) 、 x(n -2)的波形图。
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-25
n2=25
L=n2-n1+1
n=np.linspace(n1,n2,L)
x1 = np.zeros(L)
x = np.array([1,2,3,4,5,6])
N=len(x)
x1[(n0-n1):(n0-n1+N)] = x
nn1=n
nn2=nn1-2
nn3=nn1+2
plt.figure(figsize=(16,12))
plt.subplot(311)
plt.stem(n,x1)
plt.grid('on')
plt.title('x(n)')
plt.xlim(-25,25)
plt.subplot(312)
plt.stem(nn2,x1)
plt.grid('on')
plt.title('x(n+2)')
plt.xlim(-25,25)
plt.subplot(313)
plt.stem(nn3,x1)
plt.grid('on')
plt.title('x(n-2)')
plt.xlim(-25,25)
plt.show()
程序运行结果如下图所示。
（2）序列的反转
序列的反转是指 x(n) -> x(-n) ，将 x(n) 绕纵坐标轴旋转 180 度。
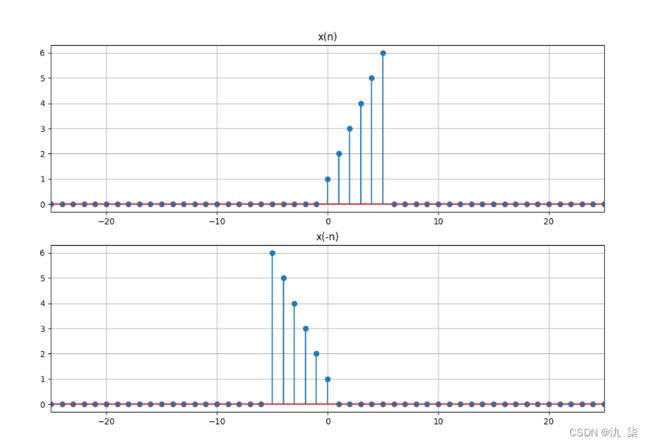
【例 2-2】已知 x(n) = {1,2,3,4,5,6}，分别画出 x(n) 和 x(-n)的波形图。
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n0=0
n1=-25
n2=25
L=n2-n1+1
n=np.linspace(n1,n2,L)
x1 = np.zeros(L)
x = np.array([1,2,3,4,5,6])
N=len(x)
x1[(n0-n1):(n0-n1+N)] = x
nn1=-n
plt.figure(figsize=(12,8))
plt.subplot(211)
plt.stem(n,x1)
plt.grid('on')
plt.title('x(n)')
plt.xlim(-25,25)
plt.subplot(212)
plt.stem(nn1,x1)
plt.grid('on')
plt.title('x(-n)')
plt.xlim(-25,25)
plt.show()
程序运行结果如图 2-2 所示。
2、两序列之间的运算
（1）相加
两序列相加是指 
，为对应位相加。
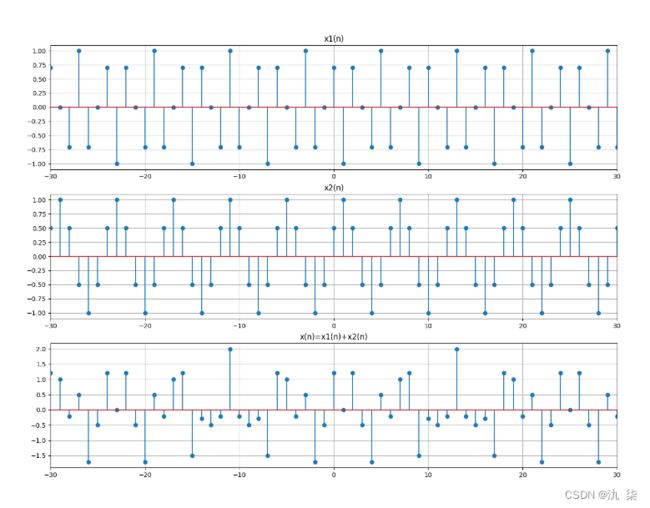
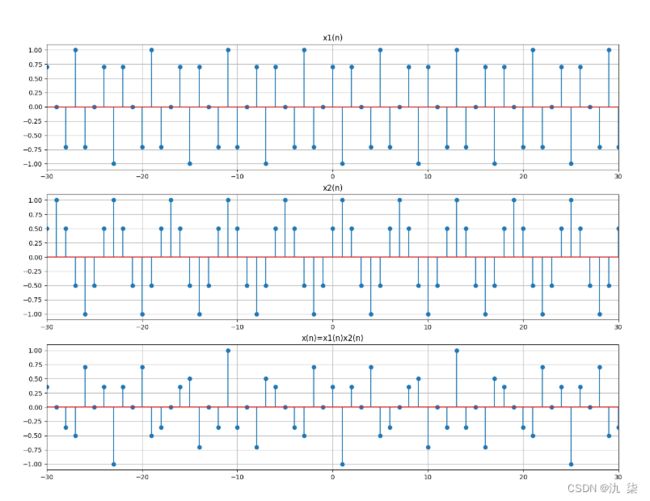
【例 2-3】已知序列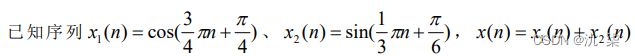 
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n1=-30
n2=30
L=n2-n1+1
PI=np.pi
w1=3/4
w2=1/3
n=np.linspace(n1,n2,L)
x1=np.cos(w1*PI*n+PI/4)
x2=np.sin(w2*PI*n+PI/6)
x=x1+x2
plt.figure(figsize=(16,12))
plt.subplot(311)
plt.stem(n,x1)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x1(n)')
plt.subplot(312)
plt.stem(n,x2)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x2(n)')
plt.subplot(313)
plt.stem(n,x)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x(n)=x1(n)+x2(n)')
plt.show()
程序运行结果如下图所示。
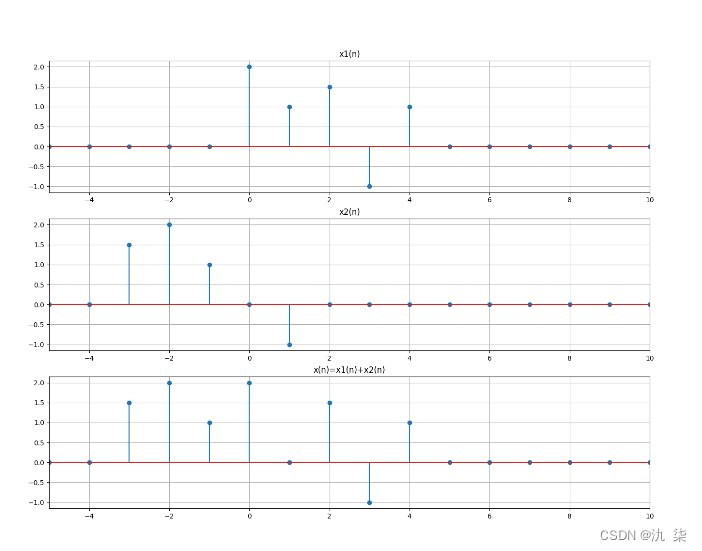
【例 2-4】
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n10=0
n20=-3
n1=-5
n2=10
L=n2-n1+1
n=np.linspace(n1,n2,L)
x1 = np.zeros(L)
x2 = np.zeros(L)
a = np.array([2,1,1.5,-1,1])
b = np.array([1.5,2,1,0,-1])
x1[(n10-n1):(n10-n1+5)] = a
x2[(n20-n1):(n20-n1+5)] = b
x3=x1+x2
plt.figure(figsize=(16,12))
plt.subplot(311)
plt.stem(n,x1)
plt.grid('on')
plt.title('x1(n)')
plt.xlim(n1,n2)
plt.subplot(312)
plt.stem(n,x2)
plt.grid('on')
plt.title('x2(n)')
plt.xlim(n1,n2)
plt.subplot(313)
plt.stem(n,x3)
plt.grid('on')
plt.title('x(n)=x1(n)+x2(n)')
plt.xlim(n1,n2)
plt.show()
程序运行结果如下图所示。
（2）相乘
两序列相加是指x(n ) = x1 (n ) * x2( n) ，为对应位相乘。
【例 2-5】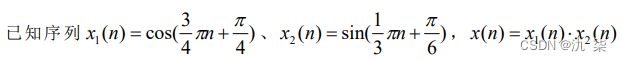
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n1=-30
n2=30
L=n2-n1+1
PI=np.pi
w1=3/4
w2=1/3
n=np.linspace(n1,n2,L)
x1=np.cos(w1*PI*n+PI/4)
x2=np.sin(w2*PI*n+PI/6)
x=x1*x2
plt.figure(figsize=(16,12))
plt.subplot(311)
plt.stem(n,x1)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x1(n)')
plt.subplot(312)
plt.stem(n,x2)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x2(n)')
plt.subplot(313)
plt.stem(n,x)
plt.xlim(-30,30)
plt.grid('on')
plt.title('x(n)=x1(n)x2(n)')
plt.show()
程序运行结果如下图所示。
【例 2-6】
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
n10=0
n20=-3
n1=-5
n2=10
L=n2-n1+1
n=np.linspace(n1,n2,L)
x1 = np.zeros(L)
x2 = np.zeros(L)
a = np.array([2, 1, 1.5, -1, 1])
b = np.array([1.5, 2, 1, 0, -1])
x1[(n10 - n1):(n10 - n1 + 5)] = a
x2[(n20 - n1):(n20 - n1 + 5)] = b
x3 = x1 * x2
plt.figure(figsize=(16, 12))
plt.subplot(311)
plt.stem(n, x1)
plt.grid('on')
plt.title('x1(n)')
plt.xlim(n1, n2)
plt.subplot(312)
plt.stem(n, x2)
plt.grid('on')
plt.title('x2(n)')
plt.xlim(n1, n2)
plt.subplot(313)
plt.stem(n, x3)
plt.grid('on')
plt.title('x(n)=x1(n)x2(n)')
plt.xlim(n1, n2)
plt.show()
程序运行结果如下图所示。
二、离散时间信号的卷积和运算
由于系统的零状态响应是激励与系统的单位序列响应的卷积，因此卷积运算在离散
时间信号处理领域被广泛应用。离散时间信号的卷积定义为：
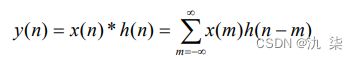
可见，离散时间信号的卷积运算是求和运算，因而常称为“卷积和”。
在 numpy 中，numpy.convolve 函数可实现两个一维数组的卷积操作，其中定义了三种模式（‘valid’，‘same’，‘full’）。设两个序列长度分别为 M 和 N，则‘valid’ 模式：输出长度为 max(M,N)-min(M,N)+1，只返回两个序列完全重合部分的点的卷积运算结果；
‘same’ 模式：输出长度为两个序列中的较长者，即 max(M,N)；
‘full’ 模式：输出长度为 M+N-1，返回所有包含重叠部分的点。
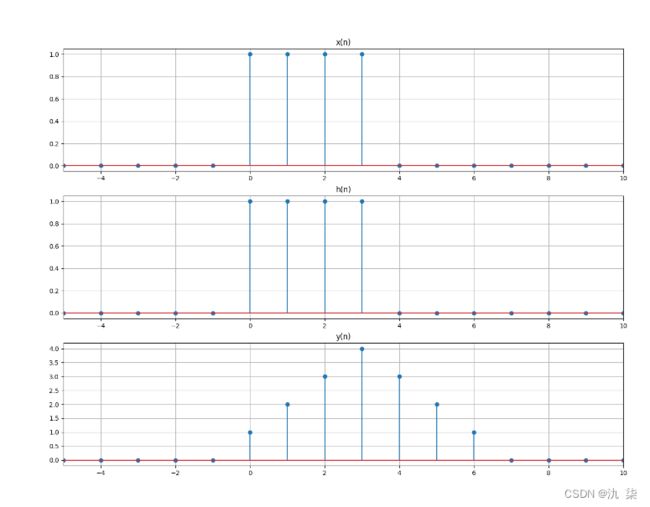
【例 2-7】
程序代码示例如下：
import numpy as np
import matplotlib.pyplot as plt
a=[1,1,1,1] #x1(n)
b=[1,1,1,1] #x2(n)
N1=len(a)
N2=len(b)
y=np.convolve(a,b,"full") #两序列的卷积 x1(n)*x2(n)
n10=0
n20=0
n1=-5
n2=10
L=n2-n1+1
n=np.linspace(n1,n2,L)
x1 = np.zeros(L)
x2 = np.zeros(L)
YL = np.zeros(L)
x1[(n10-n1):(n10-n1+N1)] = a
x2[(n20-n1):(n20-n1+N2)] = b
minN=n10+n20-n1
YL[minN:(minN+N1+N2-1)]=y
plt.figure(figsize=(16,12))
plt.subplot(311)
plt.stem(n,x1)
plt.grid('on')
plt.title('x(n)')
plt.xlim(n1,n2)
plt.subplot(312)
plt.stem(n,x2)
plt.grid('on')
plt.title('h(n)')
plt.xlim(n1,n2)
plt.subplot(313)
plt.stem(n,YL)
plt.grid('on')
plt.title('y(n)')
plt.xlim(n1,n2)
plt.show()
程序运行结果如下图所示。
