强化学习 马尔科夫决策过程(价值迭代、策略迭代、雅克比迭代、蒙特卡洛)
文章目录
- 一、马尔科夫过程Markov Decision Process(MDP)
-
- 1.简介
- 2、Markov 特性
- 3、Markov 奖励过程
-
- 符号表示
- MRPs的贝尔曼方程
- 4、Markov决策过程
-
- 符号表示
- 转化
- MRPs的贝尔曼方程
- 优化问题
- 贝尔曼最优方程
- 二、价值迭代求解
-
- 1、回顾
- 2、算法
- 3、案例
-
- 案例1
- 案例2
- 三、策略迭代求解
-
- 1、回顾
- 2、算法
- 3、案例
-
- 案例1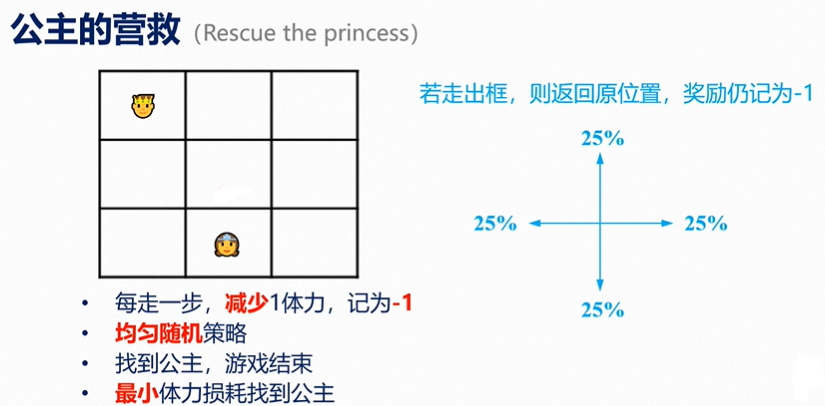
- 四、雅克比迭代法解决自举问题
-
- 1、自举问题
- 2、雅克比迭代
-
- 列主原消去法
- 雅克比迭代法
- 五、蒙特卡洛解决无模型强化学习
-
- 1、无模型
- 2、优势
- 3、原理
-
- 经验平均
- 首次访问/每次访问
- 同策略/异策略
- 批处理/增量式
- 4、案例
- 参考
一、马尔科夫过程Markov Decision Process(MDP)
1.简介
定义:无记忆的随机过程。
2、Markov 特性
1.历史状态ht={s1,s2,s3,……,st}
2.状态st有且仅有:
p ( st+1 | st )=p ( st+1 | ht )
p ( st+1 | st , at )=p ( st+1 | ht , at )
3.“考虑到现在,未来是独立于过去的”
3、Markov 奖励过程
符号表示
有四个符号 < S , P , R , γ >
S S S:有限状态集合;
P P P:状态转移概率矩阵 P s s ′ = p ( s t + 1 = s ′ ∣ s t = s ) P_{ss'}=p ( s_{t+1} = s' | s_t = s ) Pss′=p(st+1=s′∣st=s);表现为,既当前状态为 s t = s s_t=s st=s时,下一个状态变为 s t + 1 = s ′ s_{t+1}= s' st+1=s′的概率。

R R R:奖励函数 R S = E [ R t + 1 ∣ S t = s ] R_S=E[R_{t+1}|S_t=s] RS=E[Rt+1∣St=s] ,既状态单次转换取得的收益;如下图所示

γ γ γ:折扣因子/衰减系数 γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]。
回报: G t G_t Gt是从时间 t t t开始的总折扣奖励,如下式
G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + . . . = ∑ k = 0 ∞ γ k R t + k + 1 G_t=R_{t+1}+γR_{t+2}+γ^{2}R_{t+3}+...=\sum_{k=0}^{\infty}{γ^{k}R_{t+k+1}} Gt=Rt+1+γRt+2+γ2Rt+3+...=k=0∑∞γkRt+k+1
值函数: V ( s ) V(s) V(s)表示一个状态 s s s的长期价值 V ( s ) = E [ G t ∣ S t = s ] V(s)=E[G_t|S_t=s] V(s)=E[Gt∣St=s],如下图所示

MRPs的贝尔曼方程
已知,
G t = R t + 1 + γ G ( S t + 1 ) G_t=R_{t+1}+γG(S_{t+1}) Gt=Rt+1+γG(St+1)
可得,
V ( s ) = E [ R t + 1 + γ V ( S t + 1 ) ∣ S t = s ] V(s)=E[R_{t+1}+γV(S_{t+1})|S_t=s] V(s)=E[Rt+1+γV(St+1)∣St=s]
已知,
R S = E [ R t + 1 ∣ S t = S ] P s s ′ = P [ S t + 1 = s ′ ∣ S t = s ] R_S=E[R_{t+1}|S_t=S] \\ P_{ss'}=P[S_{t+1}=s'|S_t=s] RS=E[Rt+1∣St=S]Pss′=P[St+1=s′∣St=s]
可得,
V ( s ) = R S + γ ∑ s ′ ∈ S P s s ′ V ( s ′ ) V(s)=R_S+γ\sum_{s'∈S}P_{ss'}V(s') V(s)=RS+γs′∈S∑Pss′V(s′)
矩阵形式如下,

V = R + γ P V ( 1 − γ P ) V = R V = ( 1 − γ P ) − 1 R V=R+γPV\\ (1-γP)V=R\\ V=(1-γP)^{-1}R V=R+γPV(1−γP)V=RV=(1−γP)−1R
常用求解方法有动态规划、蒙特卡洛评估、时序差分学习等。
4、Markov决策过程
符号表示
有五个符号 < S , A , P , R , γ >
S S S:有限状态集合;
A A A:有限动作集合;
P P P:状态转移概率矩阵 P s s ′ a = p ( s t + 1 = s ′ ∣ s t = s , A t = a ) P_{ss'}^{a}=p (s_{t+1} = s' | s_t = s,A_t=a) Pss′a=p(st+1=s′∣st=s,At=a);状态转移矩阵 P 表现为,既当前状态为 s t = s s_t=s st=s时,下一个状态变为 s t + 1 = s ′ s_{t+1}= s' st+1=s′的概率。
R R R:奖励函数 R S a = E [ R t + 1 ∣ S t = s , A t = a ] R_S^{a}=E[R_{t+1}|S_t=s,A_t=a] RSa=E[Rt+1∣St=s,At=a] ,既状态单次转换取得的收益;
γ γ γ:折扣因子/衰减系数 γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]。
策略: π π π为给定状态的动作分布 π ( a ∣ s ) = P [ A t = a ∣ S t = s ] π(a|s)=P[A_t=a|S_t=s] π(a∣s)=P[At=a∣St=s]。
其中策略依赖于当前状态(无关历史);也是固定的(无关时间), A t ∼ π ( ⋅ ∣ S t ) A_t\thicksim π(\cdot|S_t) At∼π(⋅∣St),任意 t > 0 t>0 t>0
转化
给定一个Markov决策过程 M = < S , A , P , R , γ > M=
P s , s ′ π = ∑ a ∈ A π ( a ∣ s ) P s , s ′ a R s π = ∑ a ∈ A π ( a ∣ s ) R s a P_{s,s'}^π=\sum_{a∈A}{\pi (a|s)P_{s,s'}^a}\\ R_{s}^\pi=\sum_{a∈A}{\pi (a|s)}R_{s}^a Ps,s′π=a∈A∑π(a∣s)Ps,s′aRsπ=a∈A∑π(a∣s)Rsa
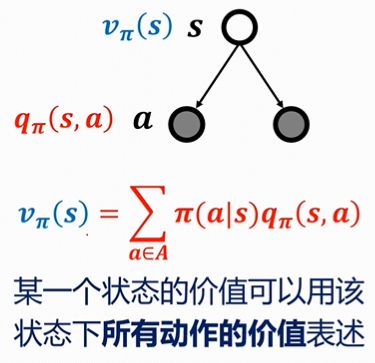
状态值函数: V ( s ) = E [ G t ∣ S t = s ] V(s)=E[G_t|S_t=s] V(s)=E[Gt∣St=s]。
动作值函数: q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=E_\pi[G_t|S_t=s,A_t=a] qπ(s,a)=Eπ[Gt∣St=s,At=a]。
MRPs的贝尔曼方程
已知,
G t = R t + 1 + γ G ( S t + 1 ) G_t=R_{t+1}+γG(S_{t+1}) Gt=Rt+1+γG(St+1)
状态值函数:
V ( s ) = E [ R t + 1 + γ V ( S t + 1 ) ∣ S t = s ] V(s)=E[R_{t+1}+γV(S_{t+1})|S_t=s] V(s)=E[Rt+1+γV(St+1)∣St=s]
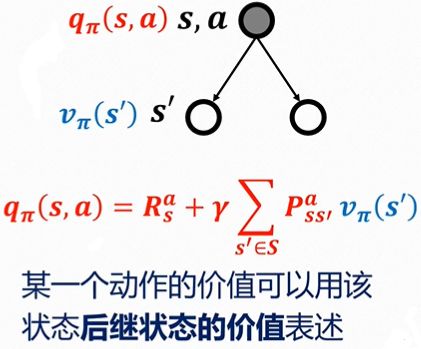
动作值函数
q π ( s , a ) = E [ R t + 1 + γ q π ( s t + 1 , a t + 1 ) ∣ S t = s , A t = a ] q_\pi(s,a)=E[R_{t+1}+γq_\pi(s_{t+1},a_{t+1})|S_t=s,A_t=a] qπ(s,a)=E[Rt+1+γqπ(st+1,at+1)∣St=s,At=a]
优化问题
最优状态值函数
v ∗ ( s ) = max π v π ( s ) v_*(s)=\max_\pi v_\pi(s) v∗(s)=πmaxvπ(s)
最优动作值函数
q ∗ ( s , a ) = max π q π ( s , a ) q_*(s,a)=\max_\pi q_\pi(s,a) q∗(s,a)=πmaxqπ(s,a)
最优策略
存在一个最优策略,使得
π ∗ ≥ a n y π \pi_*≥any\pi π∗≥anyπ
所有最优策略都能取得最优状态、动作值函数
注:若 v π ′ ( s ) ≥ v π ( s ) v_{\pi'}(s)≥v_{\pi}(s) vπ′(s)≥vπ(s)则 π ′ > π \pi'>\pi π′>π
π ∗ ( a ∣ s ) = { 1 , i f a = arg max a ∈ A q ∗ ( s , a ) 0 , o t h e r w i s e \pi_*(a|s)= \left \{ \begin{array}{ll} 1, & if a = \argmax_{a∈A} q_*(s,a)\\ 0, & otherwise \end{array} \right. π∗(a∣s)={1,0,ifa=a∈Aargmaxq∗(s,a)otherwise
贝尔曼最优方程
目标为,

得到迭代式,

求解方案有:值迭代、策略迭代、Q-Learning、Sarsa等
二、价值迭代求解
1、回顾
策略:是给定状态的动作分布 π ( a ∣ s ) = P [ A t = a ∣ S t = s ] \pi(a|s)=P[A_t=a|S_t=s] π(a∣s)=P[At=a∣St=s]随机变量,其中策略依赖于当前状态(无关历史);也是固定的(无关时间), A t ∼ π ( ⋅ ∣ S t ) A_t\thicksim π(\cdot|S_t) At∼π(⋅∣St),任意 t > 0 t>0 t>0
2、算法
算法参数:小阈值 θ > 0 \theta>0 θ>0;初始化 V ( s ) V(s) V(s),初值为0。
Loop:
△ ← 0 \triangle \gets 0 △←0
Loop for each s ∈ S s∈S s∈S:
v ← V ( s ) v \gets V(s) v←V(s)
V ( s ) ← max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] V(s) \gets \max_a \sum_{s',r}p(s',r|s,a)[r+γV(s')] V(s)←maxa∑s′,rp(s′,r∣s,a)[r+γV(s′)]
△ ← max ( △ , ∣ v − V ( s ) ∣ ) \triangle \gets \max (\triangle,|v-V(s)|) △←max(△,∣v−V(s)∣)
until △ < θ \triangle < \theta △<θ
输出确定的策略, π ≈ π ∗ \pi \approx \pi_* π≈π∗, π ( s ) = arg max a ∑ s ′ , r p ( s ′ , r ∣ s , s ) [ r + γ V ( s ′ ) ] \pi(s)=\argmax_a \sum_{s',r} p(s',r|s,s)[r+γV(s')] π(s)=aargmaxs′,r∑p(s′,r∣s,s)[r+γV(s′)]
3、案例
案例1

此处R为-1,γ为 1。
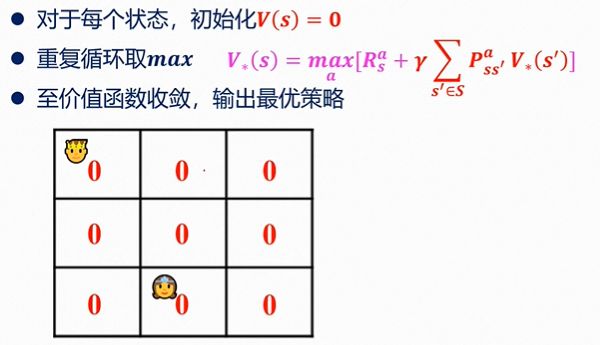
“公主”处没有下一状态,因此V(s)=0。

最终收敛为,
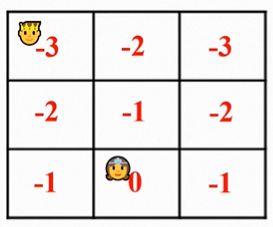
案例2
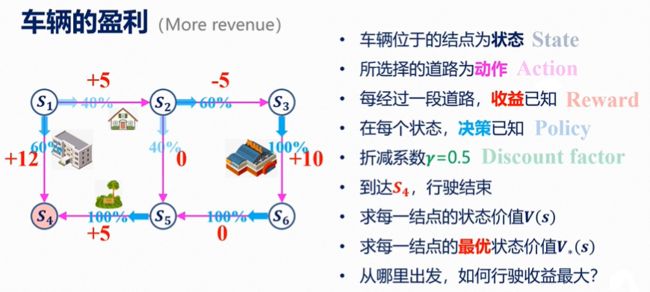
V π ( s ) = ∑ a ∈ A π ( a ∣ s ) [ R s a + γ ∑ s ′ ∈ S P s s ′ a V π ( s ′ ) ] \boldsymbol{V}_\pi {(s)}=\sum_{a \in A} \pi(a \mid s)\left[R_s^a+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^a V_\pi\left(s^{\prime}\right)\right] Vπ(s)=a∈A∑π(a∣s)[Rsa+γs′∈S∑Pss′aVπ(s′)]
可得,
V π ( S 1 ) = 40 % ( 5 + 0.5 V π ( S 2 ) ) + 60 % ( 12 + 0.5 V π ( S 4 ) ) V π ( S 6 ) = 100 % ( 0 + 0.5 V π ( S 5 ) ) V π ( S 2 ) = 60 % ( − 5 + 0.5 V π ( S 3 ) ) + 40 % ( 0 + 0.5 V π ( S 5 ) ) V π ( S 5 ) = 100 % ( 5 + 0.5 V π ( S 4 ) ) V π ( S 3 ) = 100 % ( 10 + 0.5 V π ( S 6 ) ) V π ( S 4 ) = 0 \begin{array}{ll} V_\pi\left({S}_1\right)=40 \%\left(5+0.5 V_\pi\left(S_2\right)\right)+60 \%\left(12+0.5 V_\pi\left(S_4\right)\right) & {V}_\pi\left({S}_6\right)=100 \%\left(0+0.5 V_\pi\left(S_5\right)\right) \\ {V}_\pi\left({S}_2\right)=60 \%\left(-5+0.5 V_\pi\left(S_3\right)\right)+40 \%\left(0+0.5 V_\pi\left(S_5\right)\right) & {V}_\pi\left({S}_5\right)=100 \%\left(5+0.5 V_\pi\left(S_4\right)\right) \\ {V}_\pi\left({S}_3\right)=100 \%\left(10+0.5 V_\pi\left(S_6\right)\right) & {V}_\pi\left({S}_4\right)=0 \end{array} Vπ(S1)=40%(5+0.5Vπ(S2))+60%(12+0.5Vπ(S4))Vπ(S2)=60%(−5+0.5Vπ(S3))+40%(0+0.5Vπ(S5))Vπ(S3)=100%(10+0.5Vπ(S6))Vπ(S6)=100%(0+0.5Vπ(S5))Vπ(S5)=100%(5+0.5Vπ(S4))Vπ(S4)=0
到的结果,
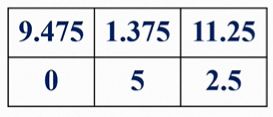
计算最优价值,
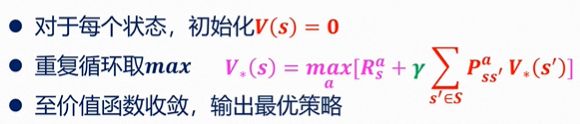
三、策略迭代求解
1、回顾
状态价值函数的贝尔曼最优方程
v ∗ ( s ) = max a [ R s a + γ ∑ s ′ ∈ S P s s ′ a v ∗ ( s ′ ) ] v_*(s)=\max _a\left[R_s^a+\gamma \sum_{s^{\prime} \in S} P_{s s^{\prime}}^a v_*\left(s^{\prime}\right)\right] v∗(s)=amax[Rsa+γs′∈S∑Pss′av∗(s′)]
动作价值函数的贝尔曼最优方程
q ∗ ( s , a ) = R s a + γ ∑ s ′ ∈ S P s s ′ a max a ′ q ∗ ( s ′ , a ′ ) {q}_*(s, a)={R}_s^a+\gamma \sum_{s^{\prime} \in S} {P}_{s s^{\prime}}^a \max _{a^{\prime}} {q}_*\left(s^{\prime}, a^{\prime}\right) q∗(s,a)=Rsa+γs′∈S∑Pss′aa′maxq∗(s′,a′)
2、算法
初始化:
小阈值 θ > 0 \theta>0 θ>0;初始化 V ( s ) V(s) V(s),初值可以为0;初始化 π ( s ) π(s) π(s)。
策略评估:
Loop:
△ ← 0 \triangle \gets 0 △←0
Loop for each s ∈ S s∈S s∈S:
v ← V ( s ) v \gets V(s) v←V(s)
V ( s ) ← max a ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ V ( s ′ ) ] V(s) \gets \max_a \sum_{s',r}p(s',r|s,a)[r+γV(s')] V(s)←maxa∑s′,rp(s′,r∣s,a)[r+γV(s′)]
△ ← max ( △ , ∣ v − V ( s ) ∣ ) \triangle \gets \max (\triangle,|v-V(s)|) △←max(△,∣v−V(s)∣)
until △ < θ \triangle < \theta △<θ
策略提升:
p o l i c y − s t a b l e ← t r u e policy-stable←true policy−stable←true
For each s ∈ S s∈S s∈S:
o l d − a c t i o n ← π ( s ) old-action←\pi(s) old−action←π(s)
π ( s ) ← arg max a ∑ s ′ , r p ( s ′ , r ∣ s , s ) [ r + γ V ( s ′ ) ] \pi(s)←\argmax_a \sum_{s',r} p(s',r|s,s)[r+γV(s')] π(s)←aargmax∑s′,rp(s′,r∣s,s)[r+γV(s′)]
If o l d − a c t i o n ≠ π ( s ) old-action \ne \pi(s) old−action=π(s),then p o l i c e − s t a b l e ← f a l s e police-stable←false police−stable←false
If p o l i c e − s t a b l e police-stable police−stable,then stop and return V ≈ v V \approx v V≈v and π ≈ v π ∗ \pi \approx v\pi_* π≈vπ∗;else go to “策略评估”
3、案例
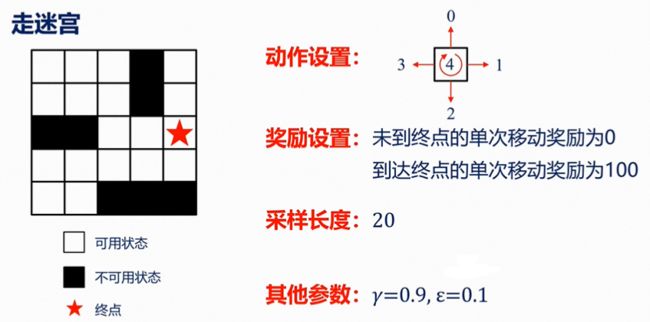
案例1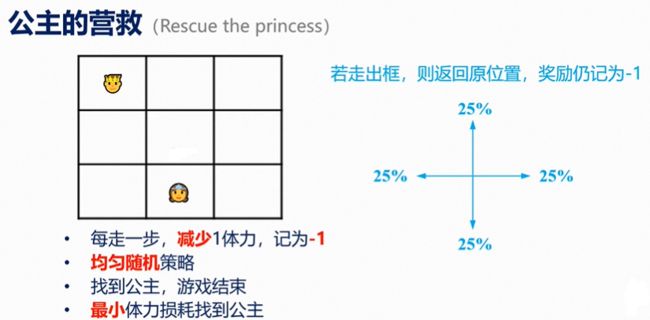
此时,
state:王子的位置
action:向四个方向走一格(走出界返回原位,但消耗体力)
reward:体力损耗
discount factor:γ=1
policy:均匀随机策略
策略评估:

最终结果(取三次迭代,因为γ为一无法收敛)
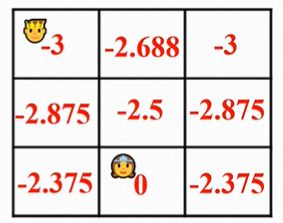
策略提升:
四、雅克比迭代法解决自举问题
1、自举问题
根据上文,可知如下公式:
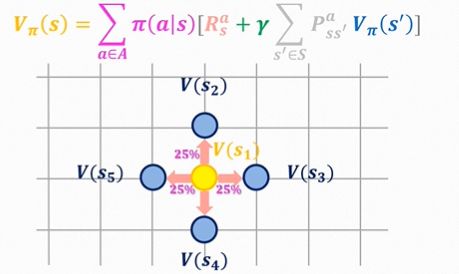
网格上每个点表示各自的状态;策略 π π π采取均匀随机策略,因此每个方向都为25%; R R R为即时奖励;由于我们为确定性策略,因此 P P P这一项都为1,。
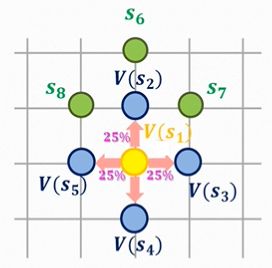
问题出现了,想要计算蓝色,那么就要求黄色;想要求黄色,就需要计算蓝色。这样“你中有我,我中有你”,的问题,便是“自举问题”。
V ( s 1 ) = 1 + 0.25 V ( s 2 ) + 0.25 V ( s 3 ) + 0.25 V ( s 4 ) + 0.25 V ( s 5 ) V ( s 2 ) = 1 + 0.25 V ( s 1 ) + 0.25 V ( s 6 ) + 0.25 V ( s 7 ) + 0.25 V ( s 8 ) V ( s 3 ) = 1 + 0.25 V ( s 1 ) + 0.25 V ( s 7 ) + 0.25 V ( s 9 ) + 0.25 V ( s 10 ) … . . . V ( s n ) = b + a 1 V ( s i ) + a 2 V ( s j ) + a 3 V ( s k ) + a 4 V ( s l ) \begin{gathered} V\left(s_1\right)=1+0.25 V\left(s_2\right)+0.25 V\left(s_3\right)+0.25 V\left(s_4\right)+0.25 V\left(s_5\right) \\ V\left(s_2\right)=1+0.25 V\left(s_1\right)+0.25 V\left(s_6\right)+0.25 V\left(s_7\right)+0.25 V\left(s_8\right) \\ V\left(s_3\right)=1+0.25 V\left(s_1\right)+0.25 V\left(s_7\right)+0.25 V\left(s_9\right)+0.25 V\left(s_{10}\right) \\ \ldots . . . \\ \boldsymbol{V}\left(\boldsymbol{s}_{\boldsymbol{n}}\right)=\boldsymbol{b}+\boldsymbol{a}_{\mathbf{1}} \boldsymbol{V}\left(\boldsymbol{s}_{\boldsymbol{i}}\right)+\boldsymbol{a}_{\mathbf{2}} \boldsymbol{V}\left(\boldsymbol{s}_{\boldsymbol{j}}\right)+\boldsymbol{a}_{\mathbf{3}} \boldsymbol{V}\left(\boldsymbol{s}_{\boldsymbol{k}}\right)+\boldsymbol{a}_{\boldsymbol{4}} \boldsymbol{V}\left(\boldsymbol{s}_{\boldsymbol{l}}\right) \end{gathered} V(s1)=1+0.25V(s2)+0.25V(s3)+0.25V(s4)+0.25V(s5)V(s2)=1+0.25V(s1)+0.25V(s6)+0.25V(s7)+0.25V(s8)V(s3)=1+0.25V(s1)+0.25V(s7)+0.25V(s9)+0.25V(s10)…...V(sn)=b+a1V(si)+a2V(sj)+a3V(sk)+a4V(sl)
由此可以得到矩阵形式:
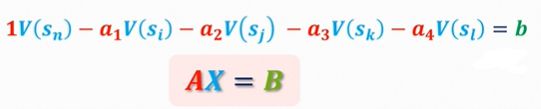
2、雅克比迭代
列主原消去法
为线性代数的基本功,只适用于低阶稠密矩阵,故不再做赘述,案例如下:
[ 1 2 3 4 5 6 7 8 8 ] [ x 1 x 2 x 3 ] = [ b 1 b 2 b 3 ] 7 x 1 + 8 x 2 + 8 x 3 = b 3 0 x 1 + 6 7 x 2 + 13 7 x 3 = b 1 − 1 7 b 3 0 x 1 + 0 x 2 + 7 14 x 3 = b 1 − 1 2 b 2 − 3 7 b 3 \begin{aligned} &{\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 8 \end{array}\right]\left[\begin{array}{l} x_1 \\ x_2 \\ x_3 \end{array}\right]=\left[\begin{array}{l} b_1 \\ b_2 \\ b_3 \end{array}\right]} \\ &7 x_1+8 x_2+8 x_3=b_3 \\ &0 x_1+\frac{6}{7} x_2+\frac{13}{7} x_3=b_1-\frac{1}{7} b_3 \\ &0 x_1+0 x_2+\frac{7}{14} x_3=b_1-\frac{1}{2} b_2-\frac{3}{7} b_3 \end{aligned} ⎣⎡147258368⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡b1b2b3⎦⎤7x1+8x2+8x3=b30x1+76x2+713x3=b1−71b30x1+0x2+147x3=b1−21b2−73b3
雅克比迭代法


将上图右上角式子进一步简化,得到迭代式(直至收敛),
X ← J X + f X←JX+f X←JX+f
其中,谱半径 ρ ( J ) < 1 ρ(J)<1 ρ(J)<1。谱半径定义为:一个矩阵中特征值绝对值最大的那个值。
五、蒙特卡洛解决无模型强化学习
1、无模型
Markov决策过程中有五个符号 < S , A , P , R , γ >
S S S:有限状态集合;
A A A:有限动作集合;
P P P:状态转移概率矩阵 P s s ′ a = p ( s t + 1 = s ′ ∣ s t = s , A t = a ) P_{ss'}^{a}=p (s_{t+1} = s' | s_t = s,A_t=a) Pss′a=p(st+1=s′∣st=s,At=a);
R R R:奖励函数 R S a = E [ R t + 1 ∣ S t = s , A t = a ] R_S^{a}=E[R_{t+1}|S_t=s,A_t=a] RSa=E[Rt+1∣St=s,At=a];
γ γ γ:折扣因子/衰减系数 γ ∈ [ 0 , 1 ] γ∈[0,1] γ∈[0,1]。
此时只知道 S S S和 A A A,其他参数未知。
2、优势
(1)能从环境中交互学习,在模拟实验中学习,无环境模型。
(2)可以只聚焦于一个子状态空间,例如我们感兴趣的状态;方法理论上需要遍历所有状态空间
(3)不需要从其他值的模拟中迭代,不自举,如果马尔可夫属性不够,可以受到更小的影响
3、原理
经验平均
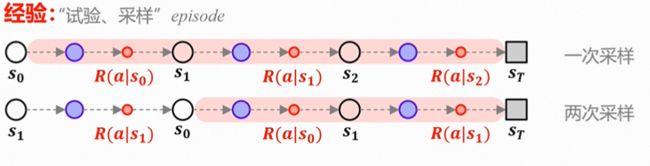
求平均:
Q 1 ( s 0 ) = R ( a ∣ s 0 ) + γ R ( a ∣ s 1 ) + γ 2 R ( a ∣ s 2 ) Q 2 ( s 0 ) = R ( a ∣ s 0 ) + γ R ( a ∣ s 1 ) } Q ( s 0 ) = Q 1 ( s 0 ) + Q 2 ( s 0 ) 2 \left.\begin{array}{l} Q_1\left(s_0\right)=R\left(a \mid s_0\right)+\gamma R\left(a \mid s_1\right)+\gamma^2 R\left(a \mid s_2\right) \\ Q_2\left(s_0\right)=R\left(a \mid s_0\right)+\gamma R\left(a \mid s_1\right) \end{array}\right\} Q\left(s_0\right)=\frac{Q_1\left(s_0\right)+Q_2\left(s_0\right)}{2} Q1(s0)=R(a∣s0)+γR(a∣s1)+γ2R(a∣s2)Q2(s0)=R(a∣s0)+γR(a∣s1)}Q(s0)=2Q1(s0)+Q2(s0)
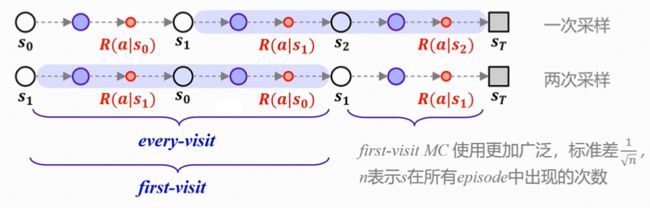
首次访问/每次访问
如图,如果每次s1出现都记录,则被称为every-visit(每次访问);只记录第一次出现,则被称为first-visit(首次访问)。
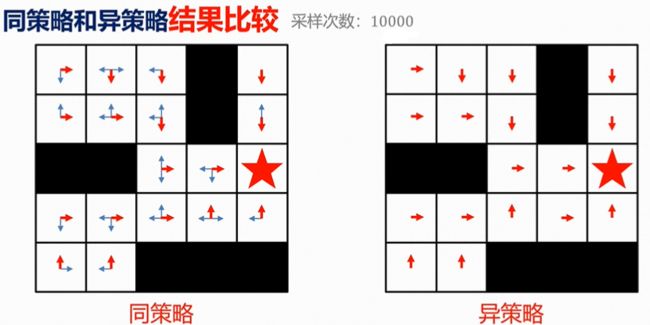
同策略/异策略
行为策略 μ μ μ(用于采样)
一般是温和的,保证一定的探索性。 ε − g r e e d y 策 略 \varepsilon-greedy策略 ε−greedy策略如下
π ( a ∣ s ) = { 1 − ε + ε ∣ A ( s ) ∣ a = argmax a Q ( s , a ) ε ∣ A ( s ) ∣ else \pi(a \mid s)=\left\{\begin{array}{cl} 1-\varepsilon+\frac{\varepsilon}{|A(s)|} & a=\operatorname{argmax}_a Q(s, a) \\ \frac{\varepsilon}{|A(s)|} & \text { else } \end{array} \right. π(a∣s)={1−ε+∣A(s)∣ε∣A(s)∣εa=argmaxaQ(s,a) else
目标策略 π π π(用于输出)
可温和可激进,是行为策略的子集。 g r e e d y 策 略 greedy策略 greedy策略如下
π ( a ∣ s ) = { 1 a = argmax a Q ( s , a ) 0 else \pi(a \mid s)= \begin{cases}1 & a=\operatorname{argmax}_a Q(s, a) \\ 0 & \text { else }\end{cases} π(a∣s)={10a=argmaxaQ(s,a) else
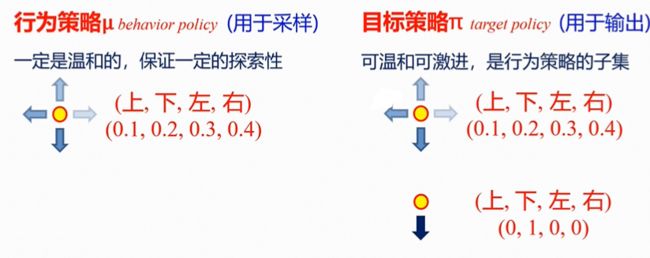

上图左侧为同策略(on-policy),右侧为异策略(off-policy)。
批处理/增量式
批处理:batch for off-line,累加求平均值,空间换时间,更快。
增量式:increment for on-line, 上 一 阶 段 平 均 值 ∗ ( N − 1 ) + K N N \frac{上一阶段平均值*(N-1)+K_N}{N} N上一阶段平均值∗(N−1)+KN,其中N为个数, K N K_N KN为第N个数的数值。
4、案例
参考
做了一些勘误
马尔可夫决策MDP过程讲解,新手也能看懂!