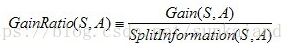机器学习算法（2）决策树

决策树

决策树是一种非常常用的非线性分类器，在介绍决策树之前，我们将先从二叉树入手。

1.二叉树决策

二叉树决策是最简单的决策树模型，由于每个非终止节点上采用线性分类器进行决策（所以也叫做二叉树分段线性分类器）——每个非终止结点有两个分支，故称为二叉树。

二叉树可以将多类问题或者多峰问题转换为多级的线性问题。

• 二叉树算法步骤

1. 采用小写g函数（参考之前的线性分类器设计方法），决策面正负侧判别；

2. 设计线性分类器，将特征空间一分为二，成为两个子空间；

3.对每个子空间，继续进行一分为二的操作，直至每个子空间中只含一类样本；

• 举个例子

• 二叉树决策特点

1. 分段线性分类器;
2. 利用二叉树决策解决两类多峰问题;
3. 二叉树各节点（分段）可以优化设计;
4. 分类器设计相对复杂一些;

需要注意的是：

由于第一个结点（或许说前面结点的权重）会对后面的权向量造成影响，所以前面的结点在设计时应该小心设计。

同时由于采用不同的结点类型会使得分类结果稍有不同，为了使得分类数不那么多，存在着一定的优化空间。

2.决策树

概念

决策树是常用的一种分级决策模型，采用决策树进行分类，可以称为多级分类器。

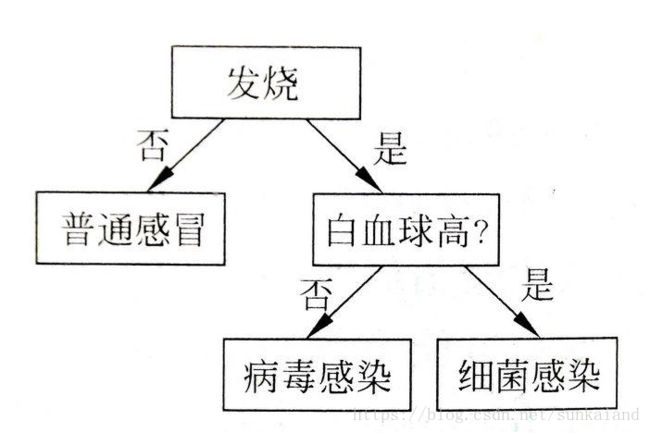
举个例子看一下：

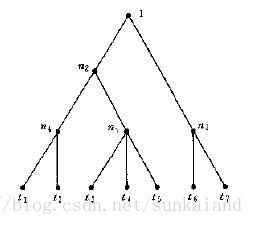
决策树模型结构

决策树T
根节点n1
非终止节点n2——n5

终止节点t1——t7

这里我们需要注意的时决策树的提出主要是为了解决非数值特征，那么什么是非数值特征呢？

描述样本的特征通常是数量值或测度。但是有些应用中样本的特征需要采用非数值的形式，称为非数值特征。例如
–物体的颜色、形状
–人的性别、民族、职业
–字符串中的字符

决策树方法就是指利用一定的训练方法，从数据中“学习”出决策规则，自动构造出决策树，并利用决策树实现分类。

举个例子：购买汽车的决策树

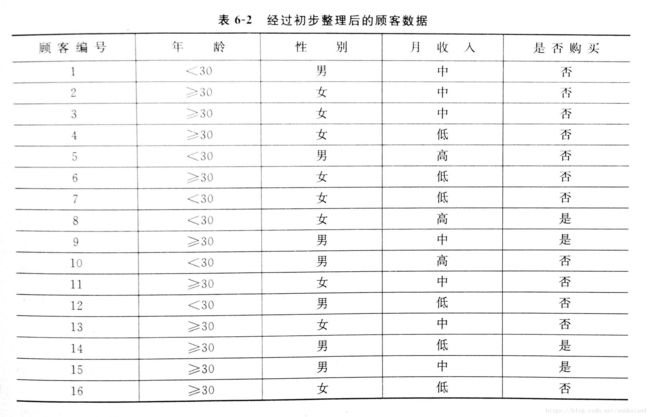
（1）原始的训练样本

（2）得到下面的非数值特征描述

（3）由ID3算法生成决策树

什么是ID3算法下面详细介绍一下。

ID3决策树算法（Interactive Dichotomizer-3）

通过选择有辨别力的特征，对数据进行划分，直到每个叶节点上只包含单一类型的数据为止。这是由Hunt等提出的概念学习系统（Concept Learning System），在此基础上，决策树的建构算法陆续提出。

算法的核心（举个例子）

1. 定义一种不纯度（一般ID3采用熵不纯度）；

熵不纯度：

；

I(16,4) = -(4/16 log2(4/16)+ 12/16 log2(12/16))；

2. 计算结点分类之后的不纯度减少量（信息增益）；

那么这一结点处的信息增益为：

3. 取不纯度减少量最大的属性作为当前节点的属性；

C4.5决策树算法

C4.5是ID3的改进算法，在ID3算法中我们以信息增益作为节点属性挑选的标准，由于单纯计算信息增益回导致算法倾向于挑选包含子节点种类多的（取值较多的特征） ，--我大致取极端情况演算了以下，确实会更偏向取子节点数更多的属性特征。

在C4.5算法中，使用了信息增益率来代替信息增益：

 其中S1到Sc是c个值的属性A分割S而形成的c个样例子集。注意分裂信息实际上就是S关于属性A的各值的熵。

决策树算法的特点

1. 解决多类问题（包括分类和对弈）；
2. 采用非数值特征；
3. 利用学习算法构建决策树；
4 .基于不纯度减少量最大化的优化算法；

过学习与剪枝

• 过学习（Over-Learning）

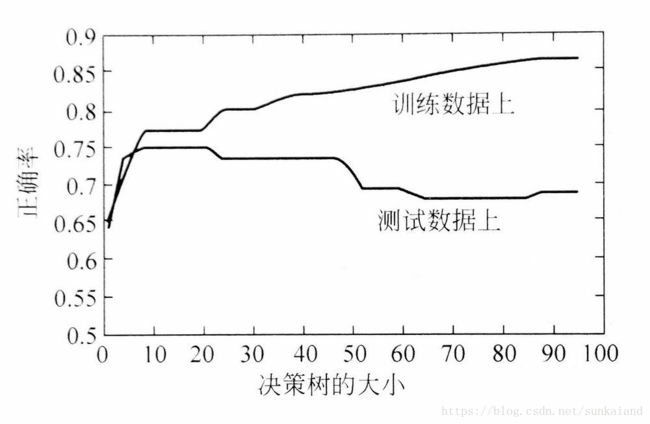
过学习是指一个算法在训练数据上表现很好，但在测试数据上或未来的新数据上的表现，与在训练数据上差别很大。

在有限样本情况下，决策树生长得很大（树枝很多或很深），则可能会抓住有限样本中由于采样的偶然性或噪声带来的假象，导致过学习。

例如：

防止过学习的主要方法：

1. 控制决策树构建算法的终止条件；

2. 对决策树进行必要的剪枝；

• 剪枝（Prunning）

剪枝分为先剪枝和后剪枝。

先剪枝：

1. 先剪枝就是控制决策树的生长；
2. 在决策树构建过程中决定某节点是否是叶节点，还是继续分枝。

后剪枝：

1. 在决策树得到充分生长之后，再对其进行修剪；

2. 对一些分支进行合并。从叶节点开始，合并具有相同父节点的叶节点后不会导致不纯度明显增加，则执行合并。

样本随机性问题

基于样本数据的分类方法都面临一个共同的问题——数据的随机性问题。

任何一次实现都是基于一个特定的样本数据集，该数据集只是所有可能数据的一次随机抽样。

决策树方法采用训练数据集构建决策树，受样本随机性的影响可能更明显。

样本随机性问题解决方法

统计学的Bootstrap策略（自举策略）——对现有样本进行重采样，产生多个样本集，用来模拟数据的随机性，在最终结果中考虑这种随机性的影响。

Bootstrap策略在机器学习方面主要应用的算法有：随机森林和Adaboost；

下面介绍随机森林。

随机森林（Random Foreast）

对现有样本进行Bootstrap，随机抽样出多个样本集，通过这些自举出来的样本集来建构多个决策树，组成决策树的“森林”。

在决策阶段的时候，对输入数据通过多棵树决策结果的投票，进行分类决策。

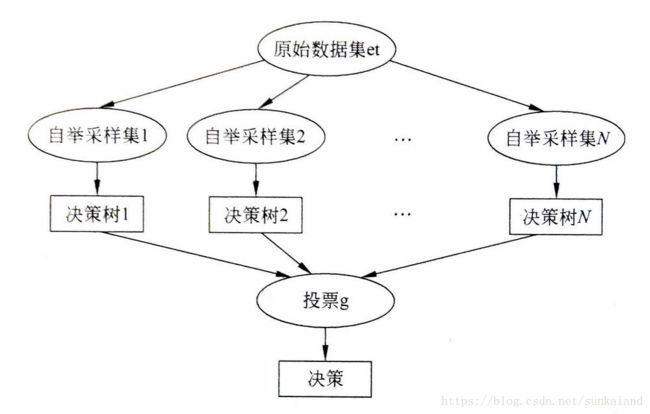
下图很好的描述了决策树的形成过程：

将上图用流程化步骤表示：

1. 对样本数据进行Bootstrap重采样，得到多个样本集。
2. 用每个重采样样本集作为训练样本集，构建决策树。

3. 得到所需数目的决策树后，对这些树的输出进行投票，得票最多的类作为随机森林的决策。

这就是关于决策数算法的描述，以后如果有添加的话再来更新。