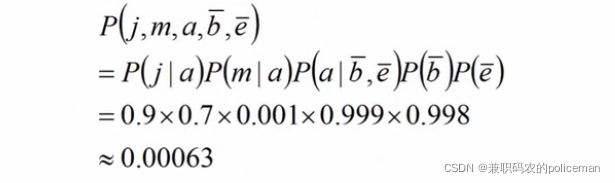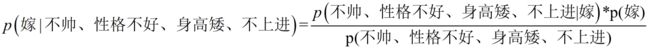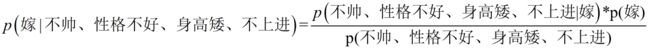机器学习:贝叶斯分类器
一、贝叶斯网络
1.(补充)先验概率与后验概率
先验概率:指根据以往经验和分析。 在实验或采样前就可以得到的概率
后验概率:指某件事已经发生,想要计算这件事发生的原因是由某个因素引起的概率。
2.(补充)极大似然估计
极大似然估计,通俗理解来说,就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!换句话说,极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。
极大似然估计中采样需满足一个重要的假设,就是所有的采样都是独立同分布的。
example:
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?
很多人马上就有答案了:70%。而其后的理论支撑是什么呢?
我们假设罐中白球的比例是p,那么黑球的比例就是1-p。因为每抽一个球出来,在记录颜色之后,我们把抽出的球放回了罐中并摇匀,所以每次抽出来的球的颜 色服从同一独立分布。
这里我们把一次抽出来球的颜色称为一次抽样。题目中在一百次抽样中,七十次是白球的,三十次为黑球事件的概率是P(样本结果|Model)。
如果第一次抽象的结果记为x1,第二次抽样的结果记为x2....那么样本结果为(x1,x2.....,x100)。这样,我们可以得到如下表达式:
P(样本结果|Model)
= P(x1,x2,…,x100|Model)
= P(x1|Mel)P(x2|M)…P(x100|M)
= p^70(1-p)^30.
好的,我们已经有了观察样本结果出现的概率表达式了。那么我们要求的模型的参数,也就是求的式中的p。
那么我们怎么来求这个p呢?
不同的p,直接导致P(样本结果|Model)的不同。
好的,我们的p实际上是有无数多种分布的。如下:
那么求出 p^70(1-p)^30为 7.8 * 10^(-31)
p的分布也可以是如下:
那么也可以求出p^70(1-p)^30为2.95* 10^(-27)
那么问题来了,既然有无数种分布可以选择,极大似然估计应该按照什么原则去选取这个分布呢?
答:采取的方法是让这个样本结果出现的可能性最大,也就是使得p^70(1-p)^30值最大,那么我们就可以看成是p的方程,求导即可!
那么既然事情已经发生了,为什么不让这个出现的结果的可能性最大呢?这也就是最大似然估计的核心。
我们想办法让观察样本出现的概率最大,转换为数学问题就是使得:
p^70(1-p)^30最大,这太简单了,未知数只有一个p,我们令其导数为0,即可求出p为70%,与我们一开始认为的70%是一致的。其中蕴含着我们的数学思想在里面。
3.概念
贝叶斯网络,又称有向无环图,是一种概率图模型。根据概率图的拓扑结构,考察一组随即变量{X1、X2、X3......Xn}及其n组条件概率分布的性质。
4.贝叶斯网络的结点与箭头
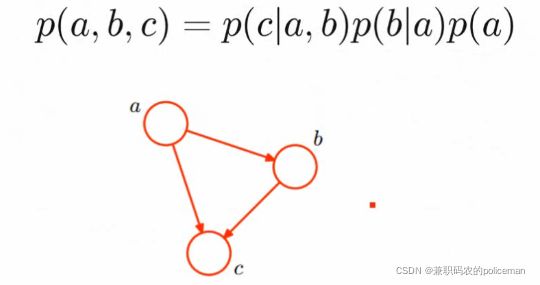
一般而言,贝叶斯网络的有向无环图中的结点表示随机变量,它们可以观察到的变量、隐变量、未知参数等。连接两个结点的箭头代表此两个随机变量是具有因果关系(或非条件独立性)。若两个结点之间以一个单箭头连接在一起,表示其中一个结点是“因”,另一个结点是“果”,两个结点就会产生一个条件概率值。
箭头表示本质不是因果关系,而是非条件独立。
5.一个“简单”的贝叶斯网络
简单:全连接的贝叶斯网络,每一对结点之间都有边连接。
模型建立非常的复杂,不利于推导甚至会产生过拟合的问题。
6.一个“正常”的贝叶斯网络
正常:有些边缺失
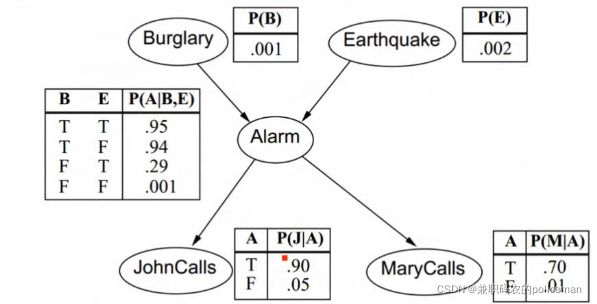
7.贝叶斯网络实例
参数的个数为1+1+4+2+2=10个
计算:John与Mary都告诉,Alarm响起,但没有发生盗窃,也没有发生地震的概率?
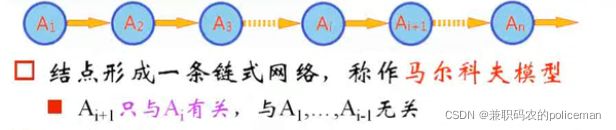
8.特殊的贝叶斯网络——马尔可夫模型
拓展还有一阶马尔可夫模型、二阶马尔可夫模型......
伪随机数发生器本质上 是 一个马尔可夫模型
斐波那契数列本质上 不是 马尔可夫模型(由于数列中每一个数都是确定的)
9.通过贝叶斯网络判断条件独立性
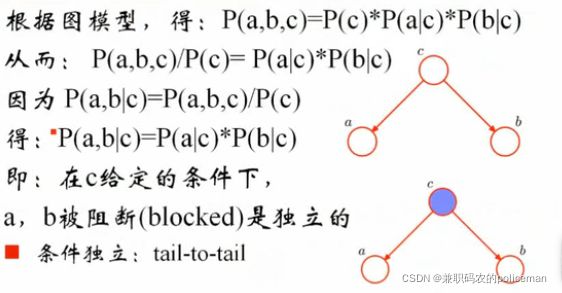
1)tail-to-tail模型 (在C 给定 的条件下,a和b被阻断,是独立的)
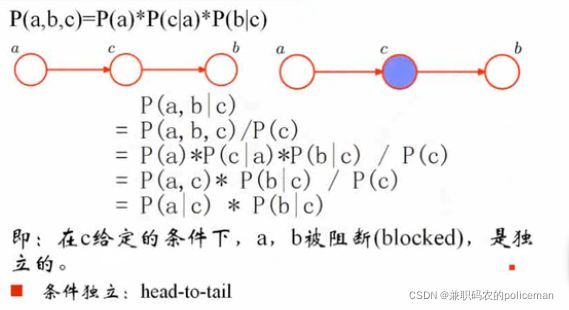
2)head-to-tail模型(在C 给定 的情况下,a和b被阻断,是独立的)
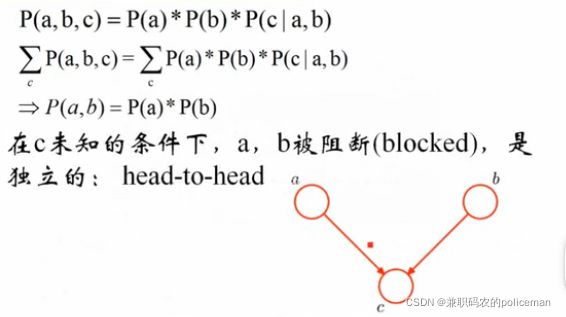
3)head-to-head模型(在C 未知 的情况下,a和b被阻断,是独立的)
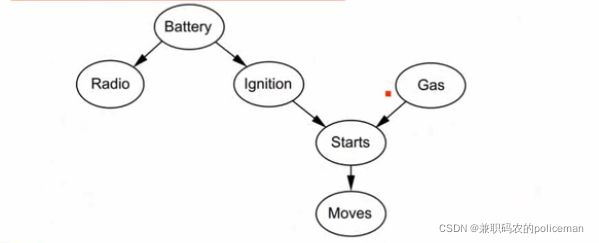
10.有向分离的举例
在给定Battery的前提下,Gas和Radio是否独立? 独立
在给定Ignition的前提下,Gas和Radio是否独立? 独立
在给定Starts的前提下,Gas和Radio是否独立? 不独立
在给定Moves的前提下,Gas和Radio是否独立? 不独立
11.隐马尔可夫模型(HMM)与马尔可夫毯(单独板块)
隐马尔可夫模型(可用于标注问题,在语音识别,NLP,生物信息,模式识别等领域被实践证明是有效的算法)是关于时间序列的概率模型,描述由一个隐藏的马尔科夫链随机生成的不可观测的状态随机序列,再由各个状态生成一个观测而产生观测随机序列的过程。
一个结点的马尔科夫毯是一个集合,在这个集合中的结点都给定的条件下,给结点条件独立于其他所有的结点。
12.贝叶斯网络的用途
在贝叶斯网络确定的结点拓扑结构和条件概率分布的前提下,可以使用该网络对未知数据计算条件概率或者后验概率,从而达到诊断、预测或者分类的目的。
诊断(例:P(病因|症状)),
预测(例:P(症状|病因)),
分类(例:MAXclassP(类别|数据))。
通过给定的样本数据,建立贝叶斯网络的拓扑结构和结点的条件概率分布参数。往往需要借助先验知识和极大似然法估计来完成。
13.贝叶斯网络的构建
先确定结点,在确定每一个结点之间是否应该有边的问题(中看不中用)
模型要按照信息流动的方向构建,要有实际的业务联系(数据、业务、逻辑相结合),即使业务中没有绝对独立,或独立原因不明确,可以靠感觉。
得到的模型不见得是最好的,要学会不断优化贝叶斯网络。
14.贝叶斯网络的推理
二、朴素贝叶斯分类器
曾被称为十大数据挖掘算法之一,往往用于文本处理中(因为文本处理特征较多)
是一个较为简单的模型,基本不会出现过拟合
【用深度学习做图像处理已经慢慢做的比较的精确了,自然语言出口是这些年比较热门的方面,有一些坑还没有填上,社会需求也非常大】
1.朴素贝叶斯的假设
1)一个特征出现的概率与其他特征(条件)独立(对于给定分类的条件下,特征独立)。
(特征独立假设要求太严了,很多时候的有些特征并不是完全独立的。但为了简化公式而做出假设,最终得出的结果拟合度还算比较高。——>为了得到更好的结果,可能还需要在算法和模型上做出更多的改进。)
2)每个特征同等重要(特征均衡性)
2.朴素贝叶斯的推导
朴素贝叶斯是基于“特征之间是独立的”这一朴素的假设,应用贝叶斯定理做出的监督学习算法。
最后一个公式表示:哪一个算的概率最大,哪一个y就是给定的结果。
3.高斯朴素贝叶斯
PS:高斯分布即正态分布,只是相同的分布不相同的叫法。
假设认为每一个特征符合高斯分布,则可以得到以下公式:
4.多项分布朴素贝叶斯
二项分布:假设某个试验是伯努利试验,成功概率用p表示,那么失败的概率为1-p。(现在进行了N次这样的试验,成功了x次,失败了N-x次,发生这种情况的概率是多少)
多项分布:多项分布是二项分布的扩展,其中随机试验的结果不是两种状态,而是K种互斥的离散状态,每种状态出现的概率为pi,p1 + p1 + … + pK = 1,在这个前提下共进行了N次试验,用x1~xK表示每种状态出现次数,x1 + x2 + …+ xK = N,称X=(x1, x2, …, xK)服从多项分布,记作X~PN(N:p1, p2,…,pn)。
5.朴素贝叶斯的参数估计
极大似然估计+贝叶斯估计(即上述的MLE估计的改进)
5.实例:以文本分类为例
1)分析
(词汇表建立最好方法:对所有邮件所有的词汇进行分开后形成邮件的单词词典)
可以使用jieba(结巴)中文分词,之后使用TF-IDF算法建立词汇表。
(隐马尔可夫模型可以进行中文分词)
在计算P(x|c)时应该使用拉普拉斯平滑:
在某一个类别当中某一个单词出现的次数很有可能出现0次(即n1=0),导致P(x|c)=0
N:代表所有单词的数目,即特征的个数。(修正分母是为了保证概率和为1)
6.实例:一个简单的例子
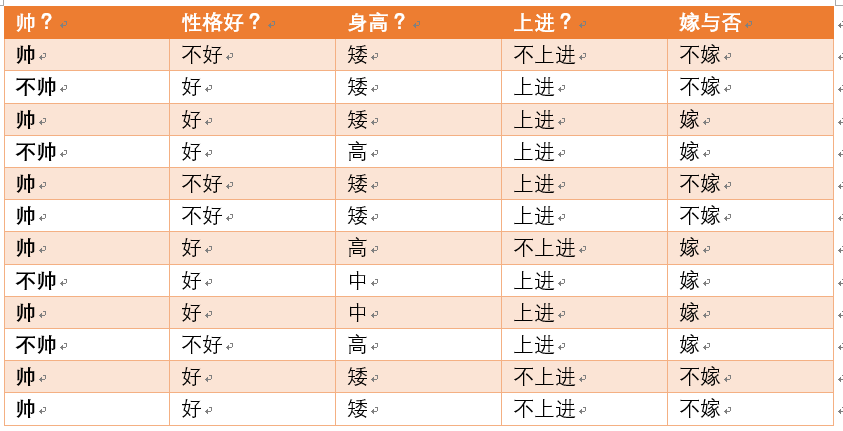
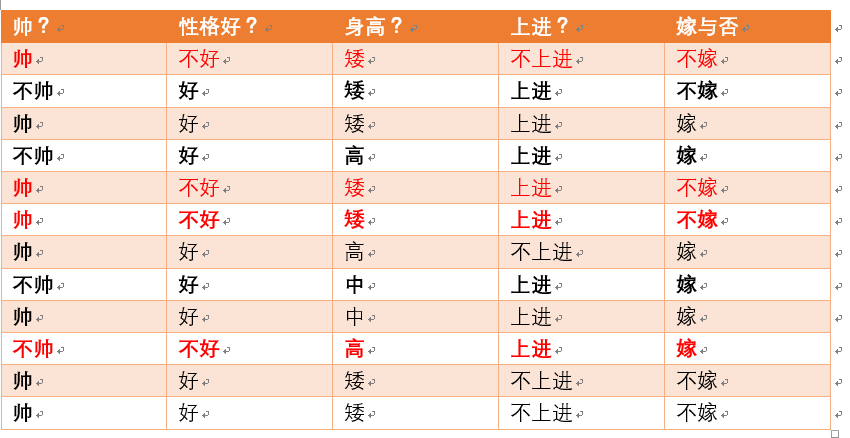
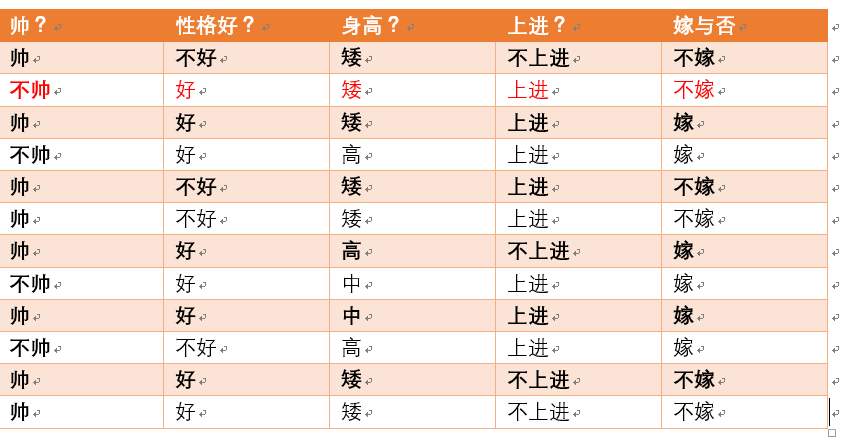
给定数据如下:
现在给我们的问题是:如果一对男女朋友,男生想女生求婚,男生的四个特点分别是不帅,性格不好,身高矮,不上进,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大,我就能给出嫁或者不嫁的答案!
这里我们联系到朴素贝叶斯公式:
我们需要求p(嫁|(不帅、性格不好、身高矮、不上进),这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量,p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)(至于为什么能求,后面会讲,那么就太好了,将待求的量转化为其它可求的值,这就相当于解决了我们的问题!)
那么这三个量是如何求得?
是根据已知训练数据统计得来,下面详细给出该例子的求解过程。
回忆一下我们要求的公式如下:
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
等等,为什么这个成立呢?学过概率论的同学可能有感觉了,这个等式成立的条件需要特征之间相互独立吧!
对的!这也就是为什么朴素贝叶斯分类有朴素一词的来源,朴素贝叶斯算法是假设各个特征之间相互独立,那么这个等式就成立了!
但是为什么需要假设特征之间相互独立呢?
1)我们这么想,假如没有这个假设,那么我们对右边这些概率的估计其实是不可做的,这么说,我们这个例子有4个特征,其中帅包括{帅,不帅},性格包括{不好,好,爆好},身高包括{高,矮,中},上进包括{不上进,上进},那么四个特征的联合概率分布总共是4维空间,总个数为2*3*3*2=36个。
36个,计算机扫描统计还可以,但是现实生活中,往往有非常多的特征,每一个特征的取值也是非常之多,那么通过统计来估计后面概率的值,变得几乎不可做,这也是为什么需要假设特征之间独立的原因。
2)假如我们没有假设特征之间相互独立,那么我们统计的时候,就需要在整个特征空间中去找,比如统计p(不帅、性格不好、身高矮、不上进|嫁),
我们就需要在嫁的条件下,去找四种特征全满足分别是不帅,性格不好,身高矮,不上进的人的个数,这样的话,由于数据的稀疏性,很容易统计到0的情况。 这样是不合适的。
根据上面俩个原因,朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
好的,上面我解释了为什么可以拆成分开连乘形式。那么下面我们就开始求解!
我们将上面公式整理一下如下:
下面我将一个一个的进行统计计算(在数据量很大的时候,根据中心极限定理,频率是等于概率的,这里只是一个例子,所以我就进行统计即可)。
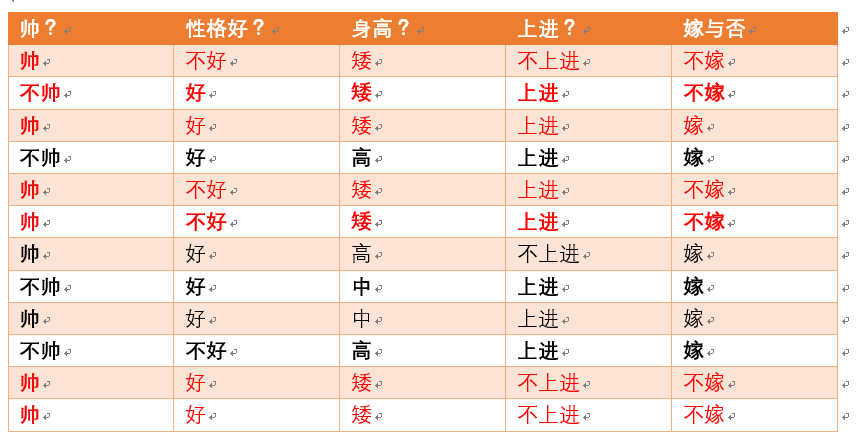
则 p(嫁) = 6/12(总样本数) = 1/2
则p(不帅|嫁) = 3/6 = 1/2
则p(性格不好|嫁)= 1/6
则p(矮|嫁) = 1/6
则p(不上进|嫁) = 1/6
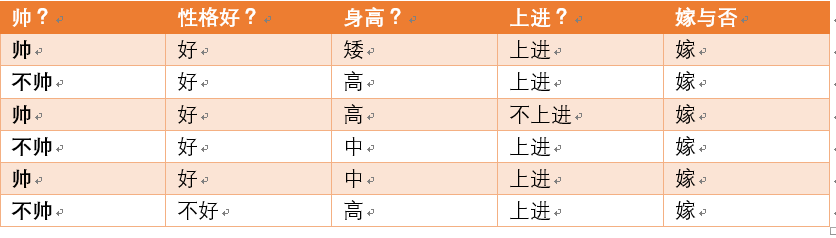
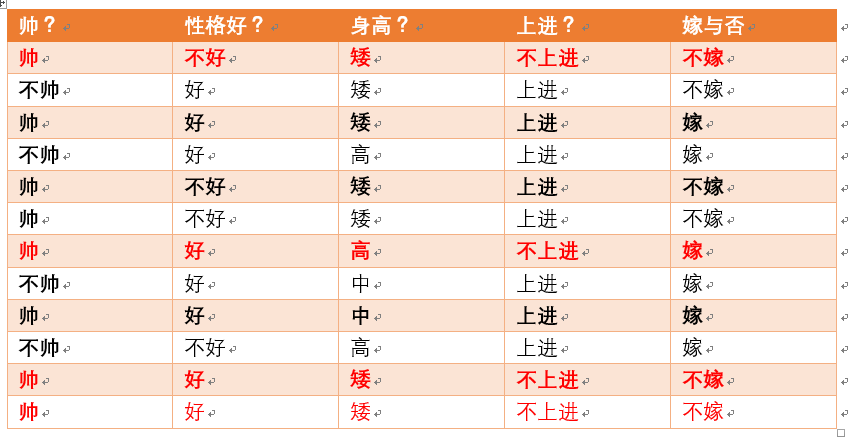
下面开始求分母,p(不帅),p(性格不好),p(矮),p(不上进)
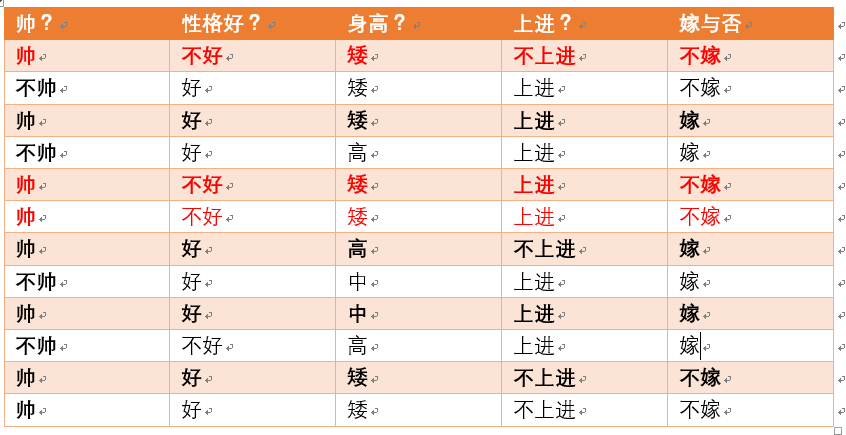
统计样本如下:
不帅统计如上红色所示,占4个,那么p(不帅) = 4/12 = 1/3
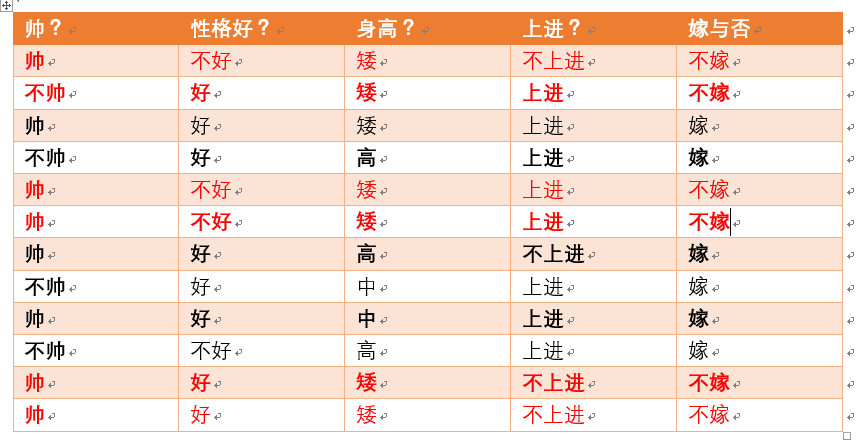
性格不好统计如上红色所示,占4个,那么p(性格不好) = 4/12 = 1/3
身高矮统计如上红色所示,占7个,那么p(身高矮) = 7/12
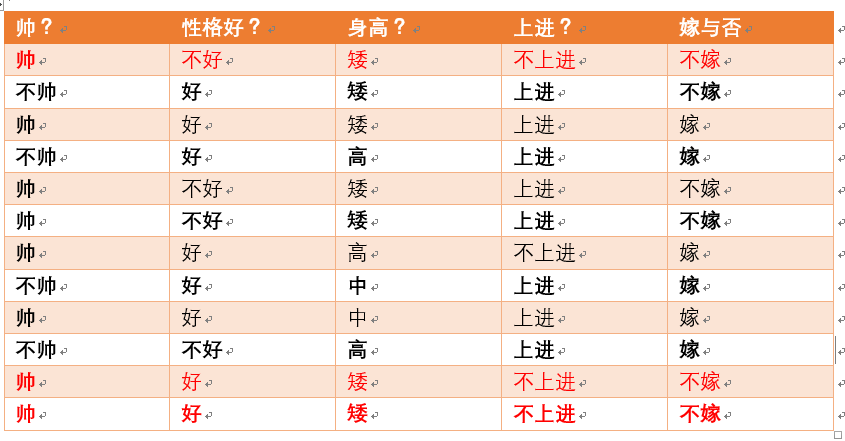
不上进统计如上红色所示,占4个,那么p(不上进) = 4/12 = 1/3
到这里,要求p(不帅、性格不好、身高矮、不上进|嫁)的所需项全部求出来了,下面我带入进去即可:
= (1/2*1/6*1/6*1/6*1/2)/(1/3*1/3*7/12*1/3)
下面我们根据同样的方法来求p(不嫁|不帅,性格不好,身高矮,不上进),完全一样的做法,为了方便理解,我这里也走一遍帮助理解。首先公式如下:
下面我也一个一个来进行统计计算,这里与上面公式中,分母是一样的,于是我们分母不需要重新统计计算!
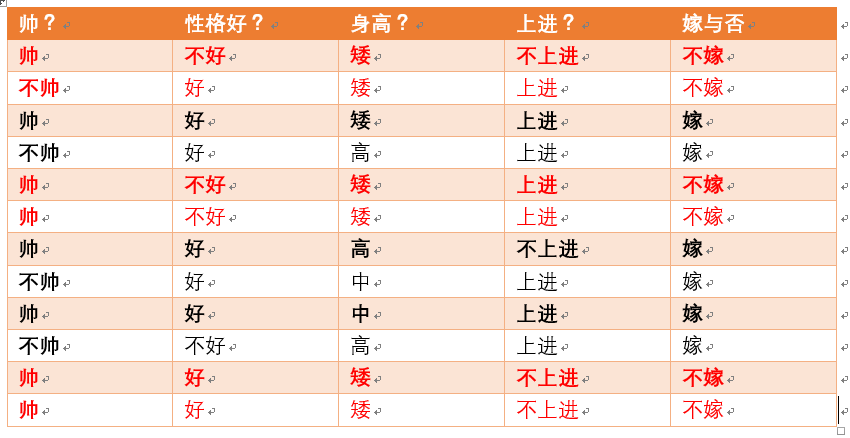
则p(不嫁)=6/12 = 1/2
则p(不帅|不嫁) = 1/6
则p(性格不好|不嫁) =3/6 = 1/2
则p(矮|不嫁) = 6/6 = 1
则p(不上进|不嫁) = 3/6 = 1/2
那么根据公式:
p (不嫁|不帅、性格不好、身高矮、不上进) = ((1/6*1/2*1*1/2)*1/2)/(1/3*1/3*7/12*1/3)
很显然(1/6*1/2*1*1/2) > (1/2*1/6*1/6*1/6*1/2)
于是有p (不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进)
所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁!!!!
7.朴素贝叶斯分类器的优缺点
1)优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
2)缺点:
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率
- 对输入数据的表达形式很敏感。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。