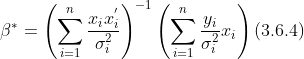- 高斯混合模型(Gaussian Mixture Model, GMM)
不想秃头的程序
神经网络语音识别人工智能深度学习网络
高斯混合模型(GaussianMixtureModel,GMM)是一种概率模型,用于表示数据点由多个高斯分布(GaussianDistribution)混合生成的过程。它广泛应用于聚类分析、密度估计、图像分割、语音识别等领域,尤其适合处理非球形簇或多模态数据。以下是GMM的详细介绍:一、核心思想GMM假设数据是由多个高斯分布混合生成的,每个高斯分布代表一个簇(Cluster),并引入隐变量(Lat
- 《现代通信原理与技术》模拟调制与解调—FM 调制实验报告
不想秃头的程序
人工智能matlab信息与通信信号处理
摘要本实验旨在通过MATLAB软件进行模拟调制与解调的实践,加深对频率调制(FrequencyModulation,FM)原理的理解,并掌握FM调制与解调的实现方法。关键词:MATLAB引言在现代通信系统中,调制技术是实现信息传输的核心方法之一。频率调制(FrequencyModulation,FM)作为一种重要的模拟调制方式,通过改变载波信号的频率来传递信息,广泛应用于广播、电视、无线通信等领域
- Spring Batch :高效处理海量数据的利器
一叶飘零_sweeeet
Springbootspringboot
SpringBatch是Spring框架中一个功能强大的批处理框架,旨在帮助开发人员轻松处理大量数据的批量操作,比如数据的导入、导出、转换以及定期的数据清理等任务。它提供了一套完善且灵活的机制,使得原本复杂繁琐的数据批处理工作变得条理清晰、易于管理和扩展。接下来,我们将全方位深入探究SpringBatch,从其核心概念、架构组成,到具体的使用示例以及在不同场景下的应用优势等,带你充分领略它的魅力所
- 鸿蒙HarmonyOS应用开发 | 深入解析 HarmonyOS Next 中的仓颉语言
一键难忘
harmonyos华为仓颉语言鸿蒙HarmonyOS
鸿蒙HarmonyOS应用开发|深入解析HarmonyOSNext中的仓颉语言在HarmonyOSNext的开发中,仓颉语言作为一种强大的编程语言,为开发者带来了全新的开发体验。本文将深入探讨仓颉语言的特点,并通过代码实例展示其在HarmonyOSNext开发中的应用。一、仓颉语言简介仓颉语言是专为HarmonyOSNext设计的编程语言,它具有简洁、高效、易读易写等特点。仓颉语言借鉴了多种现代编
- 鸿蒙仓颉开发语言实战教程:页面跳转和传参
湖北穷逼首席代表
harmonyos开发语言华为
合集-仓颉教程(25)1.详解鸿蒙仓颉开发语言中的日志打印问题05-212.鸿蒙仓颉开发语言实战教程:实现商城应用首页05-223.鸿蒙仓颉开发语言实战教程:页面跳转和传参05-254.鸿蒙仓颉语言开发教程:页面和组件的生命周期05-285.鸿蒙仓颉语言开发实战教程:购物车页面06-036.鸿蒙仓颉语言开发实战教程:商城登录页06-047.鸿蒙仓颉语言开发实战教程:商城搜索页06-058.鸿蒙仓颉
- 鸿蒙仓颉语言开发实战教程:购物车页面
王家那谁
harmonyos华为
合集-仓颉教程(25)1.详解鸿蒙仓颉开发语言中的日志打印问题05-212.鸿蒙仓颉开发语言实战教程:实现商城应用首页05-223.鸿蒙仓颉开发语言实战教程:页面跳转和传参05-254.鸿蒙仓颉语言开发教程:页面和组件的生命周期05-285.鸿蒙仓颉语言开发实战教程:购物车页面06-036.鸿蒙仓颉语言开发实战教程:商城登录页06-047.鸿蒙仓颉语言开发实战教程:商城搜索页06-058.鸿蒙仓颉
- MySQL事务深度解析:原理、优化及最佳实践
木木丰
mysqlmysql数据库javawindows
MySQL中的事务(Transaction)是数据库操作的基本单位,它代表着一组逻辑上相互关联的操作,要么全部成功,要么全部失败。这种“要么全做,要么全不做”的特性确保了数据库的完整性和一致性。事务在MySQL中扮演着至关重要的角色,特别是在处理复杂业务逻辑和并发访问时。下面将详细探讨MySQL事务的概念、使用方法、注意事项以及在实际应用中的最佳实践。一、事务的概念事务是一个不可分割的工作逻辑单元
- 深入详解:决策树算法的概念、原理、实现与应用场景
猿享天开
算法决策树机器学习
深入详解:决策树算法的概念、原理、实现与应用场景决策树(DecisionTree)是机器学习中一种直观且广泛应用的监督学习算法,适用于分类和回归任务。其树形结构易于理解,特别适合初学者。本文将从概念、原理、实现到应用场景,全面讲解决策树,并通过流程图和可视化示例增强理解,通俗易懂,帮助小白快速掌握决策树算法相关知识。1.决策树的概念1.1什么是决策树?决策树通过一系列条件判断(决策节点)将输入数据
- 2024鸿蒙OS实战开发项目大全:从入门到精通(含101个实战案例)超详细的鸿蒙实战案例
人工智能_SYBH
harmonyos华为鸿蒙开发实战项目开发入门精通
订阅专栏可获取100个实战项目源码和教程!!!(需要哪个给哪个,订阅后发邮箱,无法全给)探索鸿蒙OS开发的世界,一个非同小可的旅程即将开始。在这篇目录博客中,我将带您一览一系列令人难以置信的实战开发项目,每一个都是对HarmonyOS应用开发者的绝佳启发和宝贵资源。从基础的UI组件到复杂的分布式场景,从ArkTS的细致教学到JS的灵活运用,这一百个项目涵盖了你需要知道的HarmonyOS实战技术和
- ArkTS与仓颉语言的深度解析(鸿蒙操作系统多设备)
爱学习的小齐哥哥
仓颉华为仓颉HarmonyOS5
一、引言随着物联网和智能设备的飞速发展,多设备协同开发成为当前软件开发领域的重要课题。鸿蒙操作系统作为面向全场景的分布式操作系统,为开发者提供了ArkTS和仓颉语言两种强大的开发工具,助力实现高效的多设备应用开发。本文将全面剖析这两种语言在鸿蒙多设备开发中的应用,探讨其优势、开发环境、实现一次开发多端部署的方法以及在不同设备上的性能表现和适配策略,并结合智能驾驶应用场景进行实例分析。二、ArkTS
- [学习] PID算法原理与实践(代码示例)
极客不孤独
学习算法c语言
PID算法原理与实践文章目录PID算法原理与实践一、PID算法原理1.1PID算法概述1.定义2.应用领域3.核心目标1.2基本原理1.3数学表达离散化实现(适用于数字控制)二、实践案例(C语言)1.电机转速控制2.温度控制系统3.时钟驯服系统三、常见问题与优化1.积分饱和(Windup)问题2.噪声干扰问题3.非线性系统适配问题四、扩展方向1.数字PID与模拟PID的差异2.变参数PID(如增益
- Go Lang Fiber介绍
技术的游戏
golang开发语言后端
利用GoLangFiber进行高性能Web开发在不断发展的Web开发世界中,选择合适的框架至关重要。速度、简洁性和强大的功能集是每个开发者都追求的品质。在使用Go构建Web应用时,“Fiber”作为一个强大且轻量级的框架在众多选择中脱颖而出。在这份全面的指南中,我们将介绍GoLangFiber,涵盖其安装和设置,指导您创建一个基本的Fiber应用,并帮助您了解构成与Fiber进行Web开发旅程基础
- Go插件性能优化:如何减少内存占用和提升加载速度
Golang编程笔记
golang性能优化网络ai
Go插件性能优化:如何减少内存占用和提升加载速度关键词:Go插件、性能优化、内存占用、加载速度、编译优化、动态链接、插件架构摘要:本文将深入探讨Go语言插件的性能优化策略,从内存管理和加载速度两个核心维度出发,详细分析插件系统的运行机制,并提供一系列实用的优化技巧和最佳实践。通过本文,您将学会如何诊断插件性能瓶颈,应用有效的优化手段,并构建高效可靠的Go插件系统。背景介绍目的和范围本文旨在为Go开
- Golang Fiber框架最佳实践:如何构建企业级应用
Golang编程笔记
Golang编程笔记Golang开发实战golang开发语言后端ai
GolangFiber框架最佳实践:如何构建企业级应用关键词:Golang、Fiber框架、企业级应用、最佳实践、Web开发摘要:本文聚焦于GolangFiber框架在企业级应用构建中的最佳实践。详细介绍了Fiber框架的背景、核心概念、算法原理、数学模型等基础知识,通过具体的代码案例展示了如何搭建开发环境、实现和解读源代码。同时探讨了Fiber框架在实际应用场景中的应用,推荐了相关的学习资源、开
- 【游戏技术分享 第41期】鸿蒙游戏调用queryProducts接口返回报错1001860001,系统内部错误
游戏技术分享
鸿蒙游戏-技术分享harmonyos游戏华为
关键词IAPkit,鸿蒙,商品查询问题描述游戏集成了鸿蒙应用内支付服务,商品已在AGC后台配置,调用queryProducts接口返回系统内部错误:问题分析使用hdchilog>D:\hilog.txt命令行抓取系统全量日志,搜索IAPNAPI看到错误描述“notsupportiap”:看描述是不支持iap服务,优先从以下几点排查:agc后台是否打开应用内支付开关和激活支付协议;测试使用的华为账号
- 【鸿蒙游戏技术分享 第40期】1001860003 无效的商品信息
关键词1001860003商品管理应用内支付问题描述在游戏测试过程中,遇到商品购买报错问题"code":1001860003,"message":"BusinessError1001860003:Invalidproductinformation."问题分析1.传入的商品ID或者商品类型有误2.在AppGalleryConnect上创建的商品未提交审核或未审核通过问题处理登录AppGalleryC
- 深入研究 Golang 领域的 Fiber 框架架构
Golang编程笔记
golang架构网络ai
深入研究Golang领域的Fiber框架架构关键词:Golang、Fiber框架、架构、高性能、Web开发摘要:本文将深入探讨Golang领域的Fiber框架架构。我们会先介绍背景知识,包括目的、预期读者等。接着用通俗易懂的方式解释核心概念,如Fiber框架的各个组成部分,以及它们之间的关系。然后详细阐述核心算法原理、数学模型,通过实际代码案例展示其应用。还会介绍Fiber框架的实际应用场景、推荐
- [Python]-基础篇1- 从零开始的Python入门指南
踏雪无痕老爷子
Pythonpython开发语言
无论你是尚未接触编程的新手,还是想从其他语言转向Python的开发者,这篇文章都是你的入门课。一、Python是什么?Python是一种解释型、高级、通用型编程语言,以简洁明了、简单易用着称。它可以应用于网站开发、自动化脚本、数据分析、人工智能、系统操作等多种场景。二、如何安装Python步骤:访问Python官方网站选择目前最新的Python3.x版本下载Windows用户请务必勾选“AddPy
- RAG应用的评估(一)
AI老炮
AIGCai机器学习人工智能语言模型
前言上篇文档主要是对Advanced-RAG的定义、策略和适用场景做了一个细致的分析,那么当我们准备将一个基于大模型的RAG应用投入生产时,如何去判断这个RAG是否合理呢?下面有一些问题是需要提前考并应付的:LLM输出的不确定性会带来一定的不可预知性。一个RAG应用在投入生产之前需要科学的测试以衡量这种不可预知性。在LLM应用上线后的持续维护中,需要科学、快速、可复用的手段来衡量其改进效果,比如回
- HarmonyOS从入门到精通:WebView开发
逻极
harmonyos华为鸿蒙webviewUI前端实战
引言WebView是现代移动应用中不可或缺的组件,它使应用能够显示Web内容,实现混合开发。本文将详细介绍鸿蒙系统中WebView的开发技术,包括基本使用、性能优化和最佳实践。WebView基础知识1.WebView类型鸿蒙系统支持多种WebView实现:系统WebView自定义WebViewWeb组件2.WebView权限配置在开发WebView应用前,需要在配置文件中添加相关权限:{"modu
- Linux I/O 文件操作详解:从系统调用到实际工程应用
平凡灵感码头
linux学习linux运维服务器
一、写在前面在Linux或任何类Unix操作系统中,文件是一切的核心——无论是硬盘上的文本文件,还是串口设备、GPIO寄存器、甚至网络接口,几乎都被抽象为“文件”。理解Linux下的I/O文件操作机制,不仅是嵌入式开发的基础,也是进行系统编程与底层控制的关键。二、I/O的本质:一切皆文件Linux将外设抽象成文件的方式,统一了对各种资源的操作模型。你可以用open打开串口设备/dev/ttyS0,
- Python爬虫实战:全方位爬取知乎学习板块问答数据
Python爬虫项目
2025年爬虫实战项目python爬虫学习开发语言scrapy游戏
1.项目背景与爬取目标知乎是中国最大的知识问答社区,聚集了大量高质量的学习资源和经验分享。爬取知乎“学习”板块的问答数据,可以为学习资料整理、舆情分析、推荐系统开发等提供数据支持。本项目目标:爬取“学习”话题下的热门问答列表抓取每个问答的标题、作者、回答内容、点赞数、评论数等详细信息实现动态加载内容的抓取,包含图片和富文本避免被反爬机制限制,保证数据采集稳定结合数据分析,为后续应用打基础2.知乎“
- 人脸识别算法赋能园区无人超市安防升级
智驱力人工智能
算法人工智能边缘计算人脸识别智慧园区智慧工地智慧煤矿
人脸识别算法赋能园区无人超市安防升级正文在园区无人超市的运营管理中,传统安防手段依赖人工巡检或基础监控设备,存在响应滞后、误报率高、环境适应性差等问题。本文从技术背景、实现路径、功能优势及应用场景四个维度,阐述如何通过人脸识别检测、人员入侵算法及疲劳检测算法的协同应用,构建高效、精准的智能安防体系。一、技术背景:视觉分析算法的核心支撑人脸识别算法基于深度学习的卷积神经网络(CNN)模型,通过提取面
- 世赛背景下,中职物联网应用与服务赛项实训解决方案
武汉唯众智创
物联网世赛物联网应用与服务世界职业院校技能大赛技能大赛物联网应用
一、世赛背景与物联网应用赛项概述1.1世赛发展历程及对中职教育的影响世界技能大赛(WorldSkillsCompetition,简称世赛)自1950年创立以来,已经成为全球范围内展示职业技能水平的重要赛事。截至2024年,世赛已成功举办46届,参赛国家和地区数量不断增加,从最初的20多个发展到如今的80多个,参赛选手超过1000名。世赛涵盖了从传统制造业到现代信息技术等众多领域,其中物联网应用与服
- Memfault 简介及在Nordic nRF91 系列 DK的应用
1:Memfault是一个云平台,它允许您和您的团队持续监控设备、调试固件问题,并将OTA更新部署到您的设备群,从而以软件的速度交付硬件产品。Memfault以嵌入式优先:支持运行在任何实时操作系统(RTOS)或Android、Linux等操作系统上的嵌入式系统和设备它适用于任何设备:从功能强大的SoC一直到功能受限的MCU,Memfault都能适配您设备的可用闪存、RAM和带宽我们的SDK是专为
- OPC/MQTT工业通信软件OPLink
牛宝柱
OPLink是上海泗博自主研发的基于OPC数据采集及转发,OPC数据到MQTT通信的产品。它是基于上海泗博多年的OPC应用经验和工业通信产品的开发背景,推出的OPC/MQTT工业通信软件。软件设计简洁、实用、稳定。同时,OPLink还具备与KepwareLinkMaster相似的数据转发功能,可实现PLC设备间的自主数据通信。功能升级实时性增强:针对复杂的工业自动化环境,OPLink优化了数据传输
- GitHub Actions与AWS OIDC实现安全的ECR/ECS自动化部署
ivwdcwso
运维与云原生githubaws安全ecrecsoldcCI/CD
引言在现代云原生应用开发中,实现安全、高效的CI/CD流程至关重要。本文将详细介绍如何利用GitHubActions和AWSOIDC(OpenIDConnect)构建一个无需长期凭证的安全部署管道,将容器化应用自动部署到AmazonECR和ECS服务。架构概述整个解决方案的架构包含三个主要部分:GitHub端:代码仓库和GitHubActions工作流AWS端:OIDC身份验证、ECR容器仓库和E
- ArkTS 开发学习路径全攻略:从入门到实战
码农乐园
学习
随着HarmonyOS的持续演进,ArkTS(ArkTypeScript)已成为鸿蒙系统的主力开发语言。特别是HarmonyOSNEXT推行纯鸿蒙化后,ArkTS成为构建鸿蒙原生应用的唯一选择。本文将为你梳理一套系统化的学习路径,从语法基础到实战项目,再到系统能力调用与分布式开发,一步步带你成为合格的鸿蒙开发者。第一阶段:ArkTS语言和HarmonyOS基础入门学习目标:掌握ArkTS基础语法;
- AWS Lambda与RDS连接优化之旅
t0_54manong
编程问题解决手册aws云计算个人开发
在云计算的时代,AWSLambda与RDS的结合为开发者提供了高效且灵活的解决方案。然而,在实际应用中,我们常常会遇到一些性能瓶颈。本文将通过一个真实案例,探讨如何优化AWSLambda与RDS之间的连接,以提高API的响应速度。背景介绍最近,我们在AWS上部署了一个使用Dotnet6开发的API,它通过APIGateway暴露给外部,并连接到同VPC内的MySQLAuroraRDS数据库。部署前
- 前端用MQTT协议通信的场景和好处
CreatorRay
前端网络面试前端MQTT网络协议物联网
上家公司中前端项目有用MQTT协议和硬件通信的场景,虽然很早就听说过MQTT协议,但是这是第一次在前端项目里基于MQTT协议做网络通信。当时没了解太多,工作中只做好了代码层面的工作,并没有深入了解MQTT协议的好处和适合的应用场景。在前端项目中,应该99%的情况都会基于HTTP和WebSocket来进行网络通信,使用MQTT在前端里确实比较小众。目前可能只会在物联网项目中,需要跟硬件通信的前提下,
- 关于旗正规则引擎规则中的上传和下载问题
何必如此
文件下载压缩jsp文件上传
文件的上传下载都是数据流的输入输出,大致流程都是一样的。
一、文件打包下载
1.文件写入压缩包
string mainPath="D:\upload\"; 下载路径
string tmpfileName=jar.zip; &n
- 【Spark九十九】Spark Streaming的batch interval时间内的数据流转源码分析
bit1129
Stream
以如下代码为例(SocketInputDStream):
Spark Streaming从Socket读取数据的代码是在SocketReceiver的receive方法中,撇开异常情况不谈(Receiver有重连机制,restart方法,默认情况下在Receiver挂了之后,间隔两秒钟重新建立Socket连接),读取到的数据通过调用store(textRead)方法进行存储。数据
- spark master web ui 端口8080被占用解决方法
daizj
8080端口占用sparkmaster web ui
spark master web ui 默认端口为8080,当系统有其它程序也在使用该接口时,启动master时也不会报错,spark自己会改用其它端口,自动端口号加1,但为了可以控制到指定的端口,我们可以自行设置,修改方法:
1、cd SPARK_HOME/sbin
2、vi start-master.sh
3、定位到下面部分
- oracle_执行计划_谓词信息和数据获取
周凡杨
oracle执行计划
oracle_执行计划_谓词信息和数据获取(上)
一:简要说明
在查看执行计划的信息中,经常会看到两个谓词filter和access,它们的区别是什么,理解了这两个词对我们解读Oracle的执行计划信息会有所帮助。
简单说,执行计划如果显示是access,就表示这个谓词条件的值将会影响数据的访问路径(表还是索引),而filter表示谓词条件的值并不会影响数据访问路径,只起到
- spring中datasource配置
g21121
dataSource
datasource配置有很多种,我介绍的一种是采用c3p0的,它的百科地址是:
http://baike.baidu.com/view/920062.htm
<!-- spring加载资源文件 -->
<bean name="propertiesConfig"
class="org.springframework.b
- web报表工具FineReport使用中遇到的常见报错及解决办法(三)
老A不折腾
finereportFAQ报表软件
这里写点抛砖引玉,希望大家能把自己整理的问题及解决方法晾出来,Mark一下,利人利己。
出现问题先搜一下文档上有没有,再看看度娘有没有,再看看论坛有没有。有报错要看日志。下面简单罗列下常见的问题,大多文档上都有提到的。
1、repeated column width is largerthan paper width:
这个看这段话应该是很好理解的。比如做的模板页面宽度只能放
- mysql 用户管理
墙头上一根草
linuxmysqluser
1.新建用户 //登录MYSQL@>mysql -u root -p@>密码//创建用户mysql> insert into mysql.user(Host,User,Password) values(‘localhost’,'jeecn’,password(‘jeecn’));//刷新系统权限表mysql>flush privileges;这样就创建了一个名为:
- 关于使用Spring导致c3p0数据库死锁问题
aijuans
springSpring 入门Spring 实例Spring3Spring 教程
这个问题我实在是为整个 springsource 的员工蒙羞
如果大家使用 spring 控制事务,使用 Open Session In View 模式,
com.mchange.v2.resourcepool.TimeoutException: A client timed out while waiting to acquire a resource from com.mchange.
- 百度词库联想
annan211
百度
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=UTF-8">
<title>RunJS</title&g
- int数据与byte之间的相互转换实现代码
百合不是茶
位移int转bytebyte转int基本数据类型的实现
在BMP文件和文件压缩时需要用到的int与byte转换,现将理解的贴出来;
主要是要理解;位移等概念 http://baihe747.iteye.com/blog/2078029
int转byte;
byte转int;
/**
* 字节转成int,int转成字节
* @author Administrator
*
- 简单模拟实现数据库连接池
bijian1013
javathreadjava多线程简单模拟实现数据库连接池
简单模拟实现数据库连接池
实例1:
package com.bijian.thread;
public class DB {
//private static final int MAX_COUNT = 10;
private static final DB instance = new DB();
private int count = 0;
private i
- 一种基于Weblogic容器的鉴权设计
bijian1013
javaweblogic
服务器对请求的鉴权可以在请求头中加Authorization之类的key,将用户名、密码保存到此key对应的value中,当然对于用户名、密码这种高机密的信息,应该对其进行加砂加密等,最简单的方法如下:
String vuser_id = "weblogic";
String vuse
- 【RPC框架Hessian二】Hessian 对象序列化和反序列化
bit1129
hessian
任何一个对象从一个JVM传输到另一个JVM,都要经过序列化为二进制数据(或者字符串等其他格式,比如JSON),然后在反序列化为Java对象,这最后都是通过二进制的数据在不同的JVM之间传输(一般是通过Socket和二进制的数据传输),本文定义一个比较符合工作中。
1. 定义三个POJO
Person类
package com.tom.hes
- 【Hadoop十四】Hadoop提供的脚本的功能
bit1129
hadoop
1. hadoop-daemon.sh
1.1 启动HDFS
./hadoop-daemon.sh start namenode
./hadoop-daemon.sh start datanode
通过这种逐步启动的方式,比start-all.sh方式少了一个SecondaryNameNode进程,这不影响Hadoop的使用,其实在 Hadoop2.0中,SecondaryNa
- 中国互联网走在“灰度”上
ronin47
管理 灰度
中国互联网走在“灰度”上(转)
文/孕峰
第一次听说灰度这个词,是任正非说新型管理者所需要的素质。第二次听说是来自马化腾。似乎其他人包括马云也用不同的语言说过类似的意思。
灰度这个词所包含的意义和视野是广远的。要理解这个词,可能同样要用“灰度”的心态。灰度的反面,是规规矩矩,清清楚楚,泾渭分明,严谨条理,是决不妥协,不转弯,认死理。黑白分明不是灰度,像彩虹那样
- java-51-输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
bylijinnan
java
public class PrintMatrixClockwisely {
/**
* Q51.输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
例如:如果输入如下矩阵:
1 2 3 4
5 6 7 8
9
- mongoDB 用户管理
开窍的石头
mongoDB用户管理
1:添加用户
第一次设置用户需要进入admin数据库下设置超级用户(use admin)
db.addUsr({user:'useName',pwd:'111111',roles:[readWrite,dbAdmin]});
第一个参数用户的名字
第二个参数
- [游戏与生活]玩暗黑破坏神3的一些问题
comsci
生活
暗黑破坏神3是有史以来最让人激动的游戏。。。。但是有几个问题需要我们注意
玩这个游戏的时间,每天不要超过一个小时,且每次玩游戏最好在白天
结束游戏之后,最好在太阳下面来晒一下身上的暗黑气息,让自己恢复人的生气
&nb
- java 二维数组如何存入数据库
cuiyadll
java
using System;
using System.Linq;
using System.Text;
using System.Windows.Forms;
using System.Xml;
using System.Xml.Serialization;
using System.IO;
namespace WindowsFormsApplication1
{
- 本地事务和全局事务Local Transaction and Global Transaction(JTA)
darrenzhu
javaspringlocalglobaltransaction
Configuring Spring and JTA without full Java EE
http://spring.io/blog/2011/08/15/configuring-spring-and-jta-without-full-java-ee/
Spring doc -Transaction Management
http://docs.spring.io/spri
- Linux命令之alias - 设置命令的别名,让 Linux 命令更简练
dcj3sjt126com
linuxalias
用途说明
设置命令的别名。在linux系统中如果命令太长又不符合用户的习惯,那么我们可以为它指定一个别名。虽然可以为命令建立“链接”解决长文件名的问 题,但对于带命令行参数的命令,链接就无能为力了。而指定别名则可以解决此类所有问题【1】。常用别名来简化ssh登录【见示例三】,使长命令变短,使常 用的长命令行变短,强制执行命令时询问等。
常用参数
格式:alias
格式:ali
- yii2 restful web服务[格式响应]
dcj3sjt126com
PHPyii2
响应格式
当处理一个 RESTful API 请求时, 一个应用程序通常需要如下步骤 来处理响应格式:
确定可能影响响应格式的各种因素, 例如媒介类型, 语言, 版本, 等等。 这个过程也被称为 content negotiation。
资源对象转换为数组, 如在 Resources 部分中所描述的。 通过 [[yii\rest\Serializer]]
- MongoDB索引调优(2)——[十]
eksliang
mongodbMongoDB索引优化
转载请出自出处:http://eksliang.iteye.com/blog/2178555 一、概述
上一篇文档中也说明了,MongoDB的索引几乎与关系型数据库的索引一模一样,优化关系型数据库的技巧通用适合MongoDB,所有这里只讲MongoDB需要注意的地方 二、索引内嵌文档
可以在嵌套文档的键上建立索引,方式与正常
- 当滑动到顶部和底部时,实现Item的分离效果的ListView
gundumw100
android
拉动ListView,Item之间的间距会变大,释放后恢复原样;
package cn.tangdada.tangbang.widget;
import android.annotation.TargetApi;
import android.content.Context;
import android.content.res.TypedArray;
import andr
- 程序员用HTML5制作的爱心树表白动画
ini
JavaScriptjqueryWebhtml5css
体验效果:http://keleyi.com/keleyi/phtml/html5/31.htmHTML代码如下:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml"><head><meta charset="UTF-8" >
<ti
- 预装windows 8 系统GPT模式的ThinkPad T440改装64位 windows 7旗舰版
kakajw
ThinkPad预装改装windows 7windows 8
该教程具有普遍参考性,特别适用于联想的机器,其他品牌机器的处理过程也大同小异。
该教程是个人多次尝试和总结的结果,实用性强,推荐给需要的人!
缘由
小弟最近入手笔记本ThinkPad T440,但是特别不能习惯笔记本出厂预装的Windows 8系统,而且厂商自作聪明地预装了一堆没用的应用软件,消耗不少的系统资源(本本的内存为4G,系统启动完成时,物理内存占用比
- Nginx学习笔记
mcj8089
nginx
一、安装nginx 1、在nginx官方网站下载一个包,下载地址是:
http://nginx.org/download/nginx-1.4.2.tar.gz
2、WinSCP(ftp上传工
- mongodb 聚合查询每天论坛链接点击次数
qiaolevip
每天进步一点点学习永无止境mongodb纵观千象
/* 18 */
{
"_id" : ObjectId("5596414cbe4d73a327e50274"),
"msgType" : "text",
"sendTime" : ISODate("2015-07-03T08:01:16.000Z"
- java术语(PO/POJO/VO/BO/DAO/DTO)
Luob.
DAOPOJODTOpoVO BO
PO(persistant object) 持久对象
在o/r 映射的时候出现的概念,如果没有o/r映射,就没有这个概念存在了.通常对应数据模型(数据库),本身还有部分业务逻辑的处理.可以看成是与数据库中的表相映射的java对象.最简单的PO就是对应数据库中某个表中的一条记录,多个记录可以用PO的集合.PO中应该不包含任何对数据库的操作.
VO(value object) 值对象
通
- 算法复杂度
Wuaner
Algorithm
Time Complexity & Big-O:
http://stackoverflow.com/questions/487258/plain-english-explanation-of-big-o
http://bigocheatsheet.com/
http://www.sitepoint.com/time-complexity-algorithms/
![]() 。但在很多情况下,这个假设总是可以认为近似地成立。但是,像在
。但在很多情况下,这个假设总是可以认为近似地成立。但是,像在![]() 所指出的,仍然有许多实际问题,经过残差分析后,我们不能认为这些假设是合适的,它们的误差方差可能不相等,也可能彼此相关。这时,误差向量的协方差阵
所指出的,仍然有许多实际问题,经过残差分析后,我们不能认为这些假设是合适的,它们的误差方差可能不相等,也可能彼此相关。这时,误差向量的协方差阵![]() ,这里
,这里![]() 为一个正定阵,当然
为一个正定阵,当然![]() 往往包含有位置参数。为简单计,在这一节的讨论中,我们假定
往往包含有位置参数。为简单计,在这一节的讨论中,我们假定![]() 是完全已知的。我们要讨论的回归模型具有如下形式:
是完全已知的。我们要讨论的回归模型具有如下形式:![]()
![]() 是正定阵,于是存在n*n的正交阵P使其对角化:
是正定阵,于是存在n*n的正交阵P使其对角化:![]() ,这里
,这里![]()
![]() 是
是![]() 的特征值。记
的特征值。记![]() 。则
。则![]() ,称
,称![]() 是
是![]() 的平方根阵。用
的平方根阵。用![]() 左乘
左乘![]() ,记
,记![]() 。因为
。因为![]()
![]()
![]() 的最小二乘估计为
的最小二乘估计为![]()
![]() 为
为![]() 的广义最小二乘估计,也有一些作者称
的广义最小二乘估计,也有一些作者称![]() 为
为![]() 的
的![]() 估计,下面的定理概括了这个估计得统计性质。
估计,下面的定理概括了这个估计得统计性质。 ![]() ,有
,有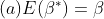
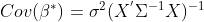
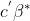 为
为 的唯一最小方差无偏估计
的唯一最小方差无偏估计![]()
![]() 设
设![]() 是
是![]() 的任一线性无偏估计,对于模型(3.6.2),我们有
的任一线性无偏估计,对于模型(3.6.2),我们有![]()
![]() 是
是![]() 的最小二乘估计,而
的最小二乘估计,而![]() 是
是![]() 的一个无偏估计,由定理3.2.2知,
的一个无偏估计,由定理3.2.2知,![]() ,并且等号成立当且仅当
,并且等号成立当且仅当![]() ,定理证毕。
,定理证毕。![]() 定理。它表明,在一般线性回归模型(3.6.1)中,广义最小二乘估计
定理。它表明,在一般线性回归模型(3.6.1)中,广义最小二乘估计![]() 是最优的。但是,如果我们把
是最优的。但是,如果我们把![]() 表达式中的
表达式中的![]() 换成单位阵
换成单位阵![]() ,则得到
,则得到![]() 。称为简单最最小二乘估计,常常简称为最小二乘估计。容易证明,对于模型(3.6.1),
。称为简单最最小二乘估计,常常简称为最小二乘估计。容易证明,对于模型(3.6.1),![]() ,即
,即![]() 仍是
仍是![]() 的无偏估计。但这时对任意线性函数
的无偏估计。但这时对任意线性函数![]() ,
,![]() 只是
只是![]() 的一个无偏估计,它未必是最优的。我们称
的一个无偏估计,它未必是最优的。我们称![]() 和
和![]() 分别为
分别为![]() 的广义最小二乘估计和(简单)最小二乘估计。根据定理3.6.1(c),对一切P*1向量c有
的广义最小二乘估计和(简单)最小二乘估计。根据定理3.6.1(c),对一切P*1向量c有![]() ,这就是说对于一般线性回归模型(3.6.1),广义最小二乘估计总是优于最小二乘估计。
,这就是说对于一般线性回归模型(3.6.1),广义最小二乘估计总是优于最小二乘估计。![]() 彼此相等。记
彼此相等。记![]() 分别为设计矩阵X的n个行向量,则容易推出,这时
分别为设计矩阵X的n个行向量,则容易推出,这时![]() 的广义最小二乘估计具有如下形式
的广义最小二乘估计具有如下形式![]() 和
和![]() 的“加权和”,而所用的权都是
的“加权和”,而所用的权都是![]() 。因此文献中常常把(3.6.4)定义的
。因此文献中常常把(3.6.4)定义的![]() 称为加权最小二乘估计。这里讲的是
称为加权最小二乘估计。这里讲的是![]() 皆已知的情况。在实际应用中,
皆已知的情况。在实际应用中,![]() 往往是未知的,这时我们可以设法求得他们的估计
往往是未知的,这时我们可以设法求得他们的估计![]() 去代替。
去代替。![]() 的形式,但这往往是十分困难的。一般我们总是从假设
的形式,但这往往是十分困难的。一般我们总是从假设![]() 入手,求得简单最小二乘估计,然后通过残差分析,对误差方差提供一些信息。另一种做法是,从问题本身的专业角度或其它方面,对误差向量提出一些特殊结构,这时误差协方差阵就具有特殊形式。
入手,求得简单最小二乘估计,然后通过残差分析,对误差方差提供一些信息。另一种做法是,从问题本身的专业角度或其它方面,对误差向量提出一些特殊结构,这时误差协方差阵就具有特殊形式。