函数与极限

1 函数与极限

1.1 映射与函数 

        从高中开始就不断学习函数，不在赘述。一个自变量只能对应一个因变量。

1.2  数列的极限

        割圆术引出极限的应用，用正多边形逼近圆的面积。

        数列极限的定义 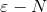： 语言描述： 

        定义法求极限通常根据  来求出N，若N可求，则极限存在，如下例：

                                                                        

        收敛数列的性质

                               定理1: 唯一性：数列收敛，极限存在则唯一。

                                        证明思路：反证法 

                                                

                               定理2: 有界性： 数列收敛，则有界。

                            注意： 无界一定不收敛，有界不一定收敛 。举例：1，-1，1，-1...

                    定理3：保号性：数列极限是a，a>0，则存在N，当n>N时，>0;

                            着直觉上是好理解的。推论 ：若数列某一项后>0,则极限为正。

                    定理4：某数列收敛与A，则其子列也收敛与A。

                            应用：两个子数列收敛与两个值，则该数列发散。一个发散的数列也有可能有收敛的子数列。

1.3  函数的极限

            极限的定义：分为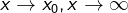两种情况。

                                   语言描述：

                                 ：

                                     .

                                 ： 

                                           

                                  单侧极限：     右极限，左极限同理。在上述的定义中，极限的定义包括左极限，右极限。

                                   注意：函数在存在的充分必要条件是 左极限右极限存在且相等。

                  函数极限的性质：与数列极限的性质类似

        1.4  无穷小与无穷大

                      无穷小：

                                定义：极限为0，简单粗暴一点。

                      无穷大：极限不存在都明白  不过∞ 包含+∞和-∞。

         1.5  极限运算法则

有限个无穷小的和是无穷小

有界函数和无穷小的乘积是无穷小 

有限个无穷小的乘积是无穷小

极限的加减乘除运算，包括先求极限在求幂次运算。

极限的复合运算 

这些问题都不大 概念不多 在于计算。

 

        1.6 极限存在准则 两个重要极限

首先 应该记住    

                夹逼准则：简单的说，三个数列  或者三个函数 g(x)

                                 则f(x)和的极限也为a。

                是这个准则下推出的。

                 采用单位圆的办法直观的推出。

                单调有界数列必有极限：这直观上是好理解的。（但是函数有极限不一定单调）

                    应用：

                      将用二项式定理展开可以看出 展开 将会比多一项，所以是单调递增的。同时也可以看出是有界的

二项式定理 

                   另外：柯西极限存在准则（极限存在的充分必要条件）：在数轴上一切具有足够大的点中，任意两点的举例小于(任意小)。

         1.7无穷小的比较

               两个无穷小之比的极限的各种情况，体现了不同无穷小趋于0的快慢。

        1.8 函数的连续性与间断点

                        连续性定义：简单的说就是这样。

                        左连续与右连续：函数左（右）极限等于函数值。

                         函数间断点：不连续点

                         第一类间断点：左极限和右极限都存在

可去间断点（左极限右极限相等不等于函数值）跳跃间断点（左右极限不相等）

                      第二类间断点：不是第一类的间断点：无穷间断点（顾名思义，极限不存在）特别的，有一种振荡间断点如下

                                                                      

         1.9 连续函数的运算与初等函数的连续性

                         1 连续函数的和差积商：一句话，都是连续的。只要保证作商时分母不为0。

                         2 反函数与复合函数的连续性：值得注意的是，反函数不仅连续性与原函数一样，单调性也一样。

                         3 函数符号f与lim运算可以交换顺序。

                         4 基本初等函数在其定义域内都是连续的。

           1.10 闭区间上联系函数的性质

                          1 有界性与最大值最小值定理：闭区间上连续函数必定有最大值最小值。

                                    好像这是显而易见的。两个条件都要满足。

                          2  零点定理

                                     函数在闭区间[a,b]上连续，且f(a)与f(b)之积异号，则（a,b）之间至少有一点，.

                                             这个定理从高中就在用。

                           3 介质定理

                                      书上的话我就不粘过来了，用自己的话说：f连续,f(m)=A,f(n)=B,介于mn之间的自变量对应的函数值肯定介于AB                                   之间。

                            4 一致连续性（在数学物理方法中会用到）

                                       这个概念很陌生：贴出定义    

                                                                  

                                          简单的说，一直连续表示只要两个自变量非常接近，函数值就可以到指定的接近程度 。

                                          注意，一致连续性定理：闭区间上一致连续，则连续。反过来不满足条件。

                                         举例理解：                                             

      

               

 

 

                         

 

                         

                                   

                                 

                                      

                               

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                 

---