常见聚类算法总结

目录

 

• 一.关于聚类
  • 什么是聚类：
  • 什么不是聚类：
  • 聚类的种类：
  • 数据间的相似度度量：
  • 簇间相似度度量：
  • 评估不同聚类方案的优劣：
  • 聚类方法的分类：
  • 聚类算法之外的处理方法：
• 二.划分式聚类方法
  • k-means：
• 三.基于密度的聚类：
  • DBSCAN 算法：
• 四.层次聚类：
  • 凝聚式聚类：
  • 分裂式聚类：
  • 治愈算法（CURE（Clustering Using Representative））：
  • 稀疏化邻近图：
  • 变色龙算法：
• 五.基于网格的聚类：
  • 子空间聚类：
• 六.基于模型的聚类
  • GMM:

---

回到顶部

一.关于聚类

什么是聚类：

聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

什么不是聚类：

● 监督分类 – 有类标签信息（通常就叫做分类）

● 简单分割 – 按姓氏的字母顺序将学生分为不同的注册组

● 查询结果 – 分组是外部规范的结果

● 图形分区 – 一些相互关联和协同作用，但领域并不相同

聚类的种类：

按照聚类方式：

 

按照排他性：在排他性聚类中，点只能属于一个聚类；在非排他性聚类中，点可能属于多个聚类，可以表示多个类或"边界"点。

按照模糊性：在模糊聚类中，一个点属于每个权重在 0 到 1 之间的聚类，权重必须总和为 1，概率聚类具有相似的特点。非模糊聚类中，每个点有唯一的预测类别

按照簇的组织方式：

基于中心的集群：簇是一组对象，使得簇中的对象比任何其他簇的中心更接近 （更相似）簇的“中心”，簇的中心通常是质心，即簇中所有点的平均值，或者是中心点，即簇中最具“代表性”的点

 

数据间的相似度度量：

闵可夫斯基距离就是Lp范数（p为正整数），而曼哈顿距离、欧式距离、切比雪夫距离分别对应

簇间相似度度量：

1）最小值：

 

2）最大值：

 

3）组平均：

 

4）质心距离

5）Ward 方法：基于SSE的增加（在层次聚类中越小合并效果越好）

 

不太容易受到噪音和异常值的影响，偏向球状星团

评估不同聚类方案的优劣：

最常见的度量是平方误差总和 (SSE，Sum of Square Error)，每个点距离自己所在簇的代表点（均值点）的距离之和，减少 SSE 的一种简单方法是增加 K，集群的数量

另一种方法：方差比率

 

N，图中的总点数

聚类方法的分类：

类别	包括的主要算法
划分方法	K-Means算法（均值）、K-medoids算法（中心点）、K-modes算法（众数）、k-prototypes算法、CLARANS（基于选择），K-Means++，bi-KMeans
层次分析	BIRCH算法（平衡迭代规约）、CURE算法（点聚类）、CHAMELEON（动态模型）,Agglomerative(凝聚式）,Divisive(分裂式)
基于密度	DBSCAN（基于高密度连接区域）、DENCLUE（密度分布函数）、OPTICS（对象排序识别）
基于网格	STING（统计信息网络）、CLIOUE（聚类高维空间）、WAVE-CLUSTER（小波变换）
基于模型	统计学方法（比如GMM）、神经网络（比如SOM（Self Organized Maps））
其他方法	量子聚类，核聚类，谱聚类

聚类算法之外的处理方法：

 

回到顶部

二.划分式聚类方法

k-means：

算法流程：

1.选择K点作为初始质心

2.重复直到质心不变

（1）通过将所有点指定给最近的质心形成K簇

（2）重新计算每个簇的质心

初始质心通常是随机选择的，产生的集群因一次运行而异。大多数收敛发生在前几次迭代中，因为通常将停止条件更改为“直到相对较少的点更改集群”

K值的选择：

 

对 k = 1,2,4,8,... 运行 k-means 算法，找到两个值 v 和 2v，它们之间的平均直径几乎没有减少，证明的 k 值位于 v/2 和 v 之间，然后在这之间使用二分搜索

处理K-means产生的空簇：选择对 SSE 贡献最大的点；从具有最高 SSE 的集群中选择一个点。并入空簇，这样下一轮空簇的中心就会移到选的点去

举例：

 

更新一轮后

 

增量更新中心的 K-means：在基本的 K-means 算法中，在所有点都分配给一个质心后更新质心

另一种方法是在分配一个点后更新质心（增量方法）

 – 每个分配更新零个或两个质心

– 更高代价

– 引入顺序依赖

– 永远不会得到一个空集群

– 可以使用“权重”来改变影响

bi-k-means算法：

初始只有一个cluster包含所有样本点；

repeat:

    从待分裂的clusters中选择一个进行二元分裂，所选的cluster应使得SSE最小（可以每一个都分裂，选SSE的最小那个）；

until 有k个cluster

k-means++算法：

k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似，改变的地方只有初始质心的选取，该部分的算法流程如下

 

K-means 的局限性：当集群尺寸或密度不同时，集群为非球形形状，数据包含异常值时，K-means 可能会有问题。一种解决方案是使用大量集群，找到集群的部分，最后结合在一起（提升k值后再使用人工方法）

 

 

回到顶部

三.基于密度的聚类：

基于密度的聚类定位由低密度区域彼此分隔的高密度区域。

 

DBSCAN 算法：

核心点：在半径 Eps 内具有超过指定数量的点 (MinPts)

边界点：点在半径 Eps 内少于 MinPts 个点，但在核心点的邻域（半径EPS的圈内）内

噪声点：既不是核心点也不是边界点的任何点

 

 

相距 Eps 之内的任意两个核心点都在同一个簇中，任何在核心点半径 Eps 内的边界点都与核心点放在同一个簇中，丢弃所有噪声点（DBSCAN是部分聚类方法，并非所有点都被聚类）

DBSCAN 实际上需要 O(n2) 时间，只要允许聚类结果的轻微不准确，运行时间就可以显着降低到 O(n)

想法是对于集群中的点，它们的第k最近邻距离大致相同；噪声点在更远的距离处具有第k最近邻距离；因此，绘制每个点到其第k最近邻距离的排序距离

 

由图：3000个点里2800个第4近邻在10以内，因此可以设置EPS=10，MinPts=4

回到顶部

四.层次聚类：

 

凝聚式聚类：

 

类似与凝聚式聚类的方法可以作为kmeans的质心初始化步骤

 

非欧空间不能选质心的问题：因为非欧空间无法求平均，可以用以下方法代替

 

可以选以上值最小的点作为集群的中心

分裂式聚类：

 

 

治愈算法（CURE（Clustering Using Representative））：

不是通过质心来表示集群，而是使用一组代表点。

 

CURE 能够更好地处理任意形状和大小的集群。向中心收缩代表点有助于避免噪声和异常值问题。

 

 

合并集群的同时，剔除孤立点

 

cure的特点：使用了采样减少计算量；使用多个点代表集群,可以匹配那些非球形的场景,而且收缩因子的使用可以减少噪音对聚类的影响

 

稀疏化邻近图：

（从图的角度理解聚类）

 

 

 

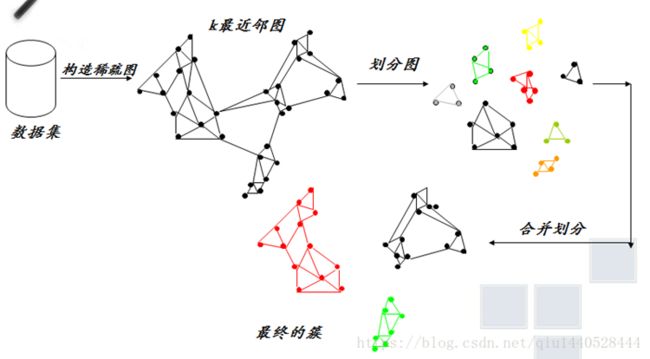
变色龙算法：

当前合并方案的局限性：层次聚类算法中现有的合并方案本质上是静态的

变色龙可以适应数据集特征寻找自然聚类，使用动态模型来衡量集群之间的相似性和互连性。

 

1. k-最近邻图Gk的构造（第一阶段）

Gk图中的每个点，表示数据集中的一个数据点。对于数据集中的每一个数据点找出它的所有k-最近邻对象，然后分别在它们之间加带权边。

如何找k-最近邻对象呢？？即找离该对象最近的k个对象点，

（定义：若点ai到另一个点bi的距离值是所有数据点到bi的距离值中k个最小值之一，则称ai是bi的k-最近邻对象。）

若一个数据点是另一个数据点的k-最近邻对象之一，则在这两点之间加一条带权边，边的权值表示这两个数据点之间的相似度，即距离越大边权值越小，则近似度越小。

2.划分图（第二阶段）

所做的一件关键的事情就是形成小簇集，由零星的几个数据点连成小簇，官方的作法是用hMetic算法根据最小化截断的边的权重和来分割k-最近邻图，然后我网上找了一些资料，没有确切的hMetic算法，借鉴了网上其他人的一些办法，于是用了一个很简单的思路，就是给定一个点，把他离他最近的k个点连接起来，就算是最小簇了。事实证明，效果也不会太差，最近的点的换一个意思就是与其最大权重的边，采用距离的倒数最为权重的大小。因为后面的计算，用到的会是权重而不是距离

3.

首先是2个略复杂的公式：

相对互连性RI

 

相对近似性RC

 

Ci,Cj表示的是i,j聚簇内的数据点的个数，EC(Ci)表示的Ci聚簇内的边的权重和，EC(Ci,Cj)表示的是连接2个聚簇的边的权重和。

那么合并的过程如下：

1、给定度量函数如下minMetric,

2、访问每个簇，计算他与邻近的每个簇的RC和RI，通过度量函数公式计算出值tempMetric。

3、找到最大的tempMetric,如果最大的tempMetric超过阈值minMetric，将簇与此值对应的簇合并

4、如果找到的最大的tempMetric没有超过阈值，则表明此聚簇已合并完成，移除聚簇列表，加入到结果聚簇中。

5、递归步骤2，直到待合并聚簇列表最终大小为空。

回到顶部

五.基于网格的聚类：

定义一组网格单元，将对象分配给单元格并计算每个单元格的密度，消除密度低于指定阈值 t 的细胞，从连续的密集细胞组形成簇。

网格单元的密度是单元中的点数除以单元的体积

 

 

子空间聚类：

去掉几个属性维度进行聚类

CLIQUE 算法：基于网格和先验的方法（如果一批点在第k维密集，那它们在k-1维也密集）

1. 找到每个属性对应的一维空间中的所有密集区间

2. K = 2 ，重复直到没有候选密集 k 维单元格

        从密集 (k – 1) 维单元格生成所有候选密集 k 维单元格

        消除密度小于阈值的细胞

        K = K + 1

3. 通过对所有连续的密集单元进行联合来查找簇。

回到顶部

六.基于模型的聚类

GMM: