直线一级倒立摆数学建模与控制仿真

学习目标：

1.推导直线型一级倒立摆的数学建模公式，得到状态空间表达式和传递函数，并分析系统的稳定性
2.采用控制算法将系统从不稳定调整到稳定状态，并用matlab和simulink仿真实现

---

学习内容：

1.建立直线型一级倒立摆的数学模型

（参考(完整版)直线一级倒立摆建模 - 百度文库 https://wenku.baidu.com/view/ca36bbba152ded630b1c59eef8c75fbfc67d9413.html）

倒立摆系统的控制问题一直是控制领域中的一个经典问题，控制的目标是通过在小车底部施加一个力u（控制量），使小车停留在预定的位置，且不超过已预先设定好的垂直偏离角度范围。一级倒立摆系统是一个不稳定的系统，需要建立其数学模型并采用控制算法调控到稳定状态。因为其为非线性问题，处理起来较为困难，因此计算过程中需要将其线性化处理。

基本参数：
小车质量M；摆杆质量m；杆长2L；转角$\theta$；小车与地面之间的摩擦系数$\mu$；重力加速度$g$
在研究过程中，应忽略空气摩擦等，而后可将倒立摆系统进行抽象化，认为其由小车和匀质刚性杆两部分组成并对这两部分进行如图所示的受力分析:

1.1.牛顿第二定理

小车X方向：$$F-Fx-f=M\ddot{x}\text{\hspace{1em}(1)}$$
摆杆X方向：$$Fx=m\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}(x-Lsin\theta )=m\frac{\mathrm{d}}{\mathrm{d}t}(\dot{x}-Lcos\theta \dot{\theta })=m\ddot{x}+mLsin\theta {\dot{\theta }}^2-mLcos\theta \ddot{\theta }\text{\hspace{1em}(2)}$$

摆杆Y方向：$$mg-Fy=m\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}(Lcos\theta )=m\frac{\mathrm{d}}{\mathrm{d}t}(-Lsin\theta \dot{\theta })=-mLcos\theta {\dot{\theta }}^2-mLsin\theta \ddot{\theta }\text{\hspace{1em}(3)}$$

摆杆力矩平衡：$$I\ddot{\theta }=FyLsin\theta +FxLcos\theta \text{\hspace{1em}(4)}$$

由于控制的目的是保持倒立摆直立，此处假设摆杆转角较小，则可以得到如下假设$sin\theta =\theta$,$cos\theta =1$ 。

式(2)(3)(4)变为
$$\begin{array}{c}Fx=m\ddot{x}+mL\theta {\dot{\theta }}^2-mL\ddot{\theta }\\ Fy=mg+mL{\dot{\theta }}^2+mL\theta \ddot{\theta }\\ I\ddot{\theta }=FxL+FyL\theta \end{array}$$

以上方程都是非线性方程，为求得解析解，需做线性化处理，有${\theta }^2=0、\dot{\theta }=0、{\dot{\theta }}^2=0$。设置摩擦力为$f=\mu \dot{x}$。设置输入控制量为u，则系统的平衡控制方程为
(2)带入(1)，(2)(3)带入(4)
$$\{\begin{array}{c}(M+m)\ddot{x}+\mu \dot{x}-mL\ddot{\theta }=u\\ (I+m{L}^2)\ddot{\theta }-mL\ddot{x}-mgL\theta =0\end{array}\text{\hspace{1em}(5)}$$

$$\begin{array}{c}\ddot{\theta }=-\frac{\mu mL}{(M+m)I+Mm{L}^2}\dot{x}+\frac{(M+m)mgL}{(M+m)I+Mm{L}^2}\theta +\frac{mL}{(M+m)I+Mm{L}^2}u\\ \ddot{x}=-\frac{\mu (I+m{L}^2)}{(M+m)I+Mm{L}^2}\dot{x}+\frac{m^{2}g{L}^2}{(M+m)I+Mm{L}^2}\theta +\frac{I+m{L}^2}{(M+m)I+Mm{L}^2}u\end{array}\text{\hspace{1em}(6)}$$

状态方程：
$$\{\begin{array}{c}\dot{X}=AX+BU\\ Y=CX+DU\end{array}$$

$$X=\left[\begin{array}{cccc}x& \dot{x}& \theta & \dot{\theta }\end{array}\right]$$

状态空间表达式：
$$\left[\begin{array}{c}\dot{x}\\ \ddot{x}\\ \dot{\theta }\\ \ddot{\theta }\end{array}\right]=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{\mu (I+m{L}^2)}{(M+m)I+Mm{L}^2}& \frac{m^{2}g{L}^2}{(M+m)I+Mm{L}^2}& 0\\ 0& 0& 0& 1\\ 0& -\frac{\mu mL}{(M+m)I+Mm{L}^2}& \frac{(M+m)mgL}{(M+m)I+Mm{L}^2}& 0\end{array}\right].\left[\begin{array}{c}x\\ \dot{x}\\ \theta \\ \dot{\theta }\end{array}\right]+\left[\begin{array}{c}0\\ \frac{I+m{L}^2}{(M+m)I+Mm{L}^2}\\ 0\\ \frac{mL}{(M+m)I+Mm{L}^2}\end{array}\right].u\text{\hspace{1em}(7)}$$

$$Y=\left[\begin{array}{c}x\\ \theta \end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right].\left[\begin{array}{c}x\\ \dot{x}\\ \theta \\ \dot{\theta }\end{array}\right]+\left[\begin{array}{c}0\\ 0\end{array}\right].u\text{\hspace{1em}(8)}$$
式中，$x$是小车的位移；$\dot{x}$是小车的速度；$\theta$是摆杆的角度；$\dot{\theta }$是摆杆的角速度；u是输入；Y是输出。

1.2.拉格朗日法

从能量的角度出发建立系统的运动方程，即系统的动能、势能以及外力。定义第二类拉格朗日方程为：
$$\begin{array}{c}L=T-V\\ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\frac{\partial L}{\partial {\dot{q}}_i}-\frac{\partial L}{\partial q_i}=W_i(i=1,...,k)\end{array}\text{\hspace{1em}(9)}$$

其中，$T$是系统的动能，$V$是系统的势能，$W_i$对应于广义坐标$q_i$的非有势力的广义力。（有势力是指作用在物体的力所做功仅与力作用点的起始位置和终了位置有关，而与其作用点经过的路径无关的力。）

动能：
$$\begin{array}{c}{T}_c=\frac{1}{2}M{\dot{x}}^2\\ T_b=\frac{1}{2}I{\dot{\theta }}^2+\frac{1}{2}m\left\{{\left[\frac{\mathrm{d}}{\mathrm{d}t}(x-Lsin\theta )\right]}^2+{\left[\frac{\mathrm{d}}{\mathrm{d}t}(Lcos\theta )\right]}^2\right\}\\ =\frac{1}{2}I{\dot{\theta }}^2+\frac{1}{2}m({\dot{x}}^2-2Lcos\theta \dot{\theta }\dot{x}+L^2{\dot{\theta }}^2)\end{array}\text{\hspace{1em}(10)}$$

势能
$$\begin{array}{c}{V}_c=0\\ V_b=mgLcos\theta \end{array}\text{\hspace{1em}(11)}$$

外力
$$\begin{array}{c}{W}_c=F-f\\ W_b=0\end{array}\text{\hspace{1em}(12)}$$

总动能、势能、外力
$$\begin{array}{c}T=T_c+T_b=\frac{1}{2}M{\dot{x}}^2+\frac{1}{2}I{\dot{\theta }}^2+\frac{1}{2}m({\dot{x}}^2-2Lcos\theta \dot{\theta }\dot{x}+L^2{\dot{\theta }}^2)\\ V=V_c+V_b=mgLcos\theta \\ W=W_c+W_b=F-f\end{array}\text{\hspace{1em}(13)}$$

结合式(9)计算lagrange方程求解
$$\begin{array}{c}L=T-V=\frac{1}{2}M{\dot{x}}^2+\frac{1}{2}I{\dot{\theta }}^2+\frac{1}{2}m({\dot{x}}^2-2Lcos\theta \dot{\theta }\dot{x}+L^2{\dot{\theta }}^2)-mgLcos\theta \\ =\frac{1}{2}(M+m){\dot{x}}^2+\frac{1}{2}(I+m{L}^2){\dot{\theta }}^2-mLcos\theta \dot{\theta }\dot{x}-mgLcos\theta \end{array}\text{\hspace{1em}(14)}$$

对$x$求导
$$\begin{array}{c}\frac{\partial L}{\partial \dot{x}}=(M+m)\dot{x}-mLcos\theta \dot{\theta }\\ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\frac{\partial L}{\partial \dot{x}}=(M+m)\ddot{x}+mLsin\theta {\dot{\theta }}^2-mLcos\theta \ddot{\theta }\\ \frac{\partial L}{\partial x}=0\\ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\frac{\partial L}{\partial \dot{x}}-\frac{\partial L}{\partial x}=(M+m)\ddot{x}+mLsin\theta {\dot{\theta }}^2-mLcos\theta \ddot{\theta }=F-f\end{array}\text{\hspace{1em}(15)}$$

对$\theta$求导
$$\begin{array}{c}\frac{\partial L}{\partial \dot{\theta }}=(I+m{L}^2)\dot{\theta }-mLcos\theta \dot{x}\\ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\frac{\partial L}{\partial \dot{\theta }}=(I+m{L}^2)\ddot{\theta }+mLsin\theta \dot{\theta }\dot{x}-mLcos\theta \ddot{x}\\ \frac{\partial L}{\partial \theta }=mLsin\theta \dot{\theta }\dot{x}+mgLsin\theta \\ \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\frac{\partial L}{\partial \dot{\theta }}-\frac{\partial L}{\partial \theta }=(I+m{L}^2)\ddot{\theta }+mLsin\theta \dot{\theta }\dot{x}-mLcos\theta \ddot{x}-mLsin\theta \dot{\theta }\dot{x}-mgLsin\theta =0\end{array}\text{\hspace{1em}(16)}$$

控制方程
$$\{\begin{array}{c}(M+m)\ddot{x}+mLsin\theta {\dot{\theta }}^2-mLcos\theta \ddot{\theta }=F-f\\ (I+m{L}^2)\ddot{\theta }+mLsin\theta \dot{\theta }\dot{x}-mLcos\theta \ddot{x}-mLsin\theta \dot{\theta }\dot{x}-mgLsin\theta =0\end{array}\text{\hspace{1em}(17)}$$

假设$sin\theta =\theta$，$cos\theta =1$，${\dot{\theta }}^2=0$，$\theta \dot{\theta }=0$
$$\{\begin{array}{c}(M+m)\ddot{x}-mL\ddot{\theta }+\mu \dot{x}=u\\ (I+m{L}^2)\ddot{\theta }-mL\ddot{x}-mgL\theta =0\end{array}\text{\hspace{1em}(18)}$$

可以发现该式与牛顿第二定理计算得到的结果(5)是一致的，说明两种方法都可以得到正确的动力学方程式。
最后对式(18)进行拉普拉斯变换：
$$\{\begin{array}{c}(M+m)X(s)s^2-mL\Theta (s)s^2+\mu X(s)s=U(s)\\ (I+m{L}^2)\Theta (s)s^2-mLX(s)s^2-mgL\Theta (s)=0\end{array}\text{\hspace{1em}(18)}$$

可以得到摆杆转角与输入力的开环传递函数：
$$\begin{array}{c}{G}_{rod}(s)=\frac{\Theta (s)}{U(s)}=\frac{mL{s}^2}{[(M+m)I+Mm{I}^2]s^4+\mu (I+m{L}^2)s^3-(M+m)mgL{s}^2-\mu mgLs}\end{array}\text{\hspace{1em}(19)}$$

小车位移与输入力的开环传递函数：
$$\begin{array}{c}{G}_{car}(s)=\frac{X(s)}{U(s)}=\frac{(I+m{L}^2)s^2-mgL}{[(M+m)I+Mm{L}^2]s^4+\mu (I+m{L}^2)s^3-(M+m)mgL{s}^2-\mu mgLs}\end{array}\text{\hspace{1em}(20)}$$

2.稳定性、能控性和能观性分析

2.1.稳定性

若控制系统在初始条件和扰动作用下 ，其瞬态响应随时间的推移而逐渐衰减并趋于原点（平衡工作点），则称该系统是稳定的。反之‚如果控制系统受到扰动作用后，其瞬态响应随时间的推移而发散，输出呈持续振荡过程‚或者输出无限制地偏离平衡状态，则称该系统是不稳定的。

李雅普诺夫稳定性判据阶线性时不变连续系统$\dot{X}=AX+BU$的平衡状态$x_e=0$渐近稳定的充要条件是矩阵$A$的所有特征值均具有负实部，即系统的极点都要位于负半平面。

2.2.能控性

线性连续定常系统$\dot{X}=AX+BU$，如果存在一个分段连续的输入$u(t)$‚能在有限的时间区间$[t_0,t_f]$内‚使系统由某一初始状态‚$x(t_0)$转移到指定的任意终端状态$x(y_f)$，‚则称此状态是能控的。若系统的所有状态都是能控的，‚则称此系统是状态完全能控的‚或简称系统是能控的。

可控性判别矩阵：由$A,B$构成的可控性判别矩阵满秩。
$rank(Q_c)=n$，其中$Q_c=\left[\begin{array}{ccc}B& AB& A^{2}B\cdots A^{n-1}B\end{array}\right]$，$n$是系统的维数。

2.3.能观性

对于输出方程$Y=CX$，存在一有限时间$[t_0,t_f]$，使得在期间测量得到的$y(t)$，能唯一地确定系统的初始状态‚$x(t_0)$，‚则称此系统是可观测的。若系统的每一个状态都是可观测的，则称系统是状态完全可观测的，简称可观测的。

其判别条件为：由$A,C$构成的可观测性判别矩阵满秩。
$rank(Q_0)=n$，其中$Q_0=\left[\begin{array}{ccc}C& CA& C{A}^2\cdots C{A}^{n-1}\end{array}\right]$，$n$是系统的维数。

2.4.倒立摆系统状态分析

各参数给定为：

小车质量	M = 0.5 kg	摆杆质量	m = 0.5 kg
地面摩擦系数	$\mu$ = 0.1	小车惯性矩	I = 0.006
重力加速度	g = 9.8	小车长度	L = 0.3 m

带入参数可以求得开环传递函数为
$$\begin{array}{c}{G}_{rod}(s)=\frac{-0.15s^2}{-0.0285s^4-0.0051s^3+1.47s^2+0.147s}\\ G_{car}(s)=\frac{-0.051s^2+1.47}{-0.0285s^4-0.0051s^3+1.47s^2+0.147s}\end{array}$$

这里求极点的方法可以直接用matlab的函数tf2zp(num,den)，num和den对应传递函数和分子和分母系数。或是用solve函数求解分母的跟。计算得到系统极点：[-7.22，-0.1，0，7.14]，有两个极点位于右半平面，系统不稳定。

状态方程：
$$\begin{array}{c}A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -0.1789& 7.7368& 0\\ 0& 0& 0& 1\\ 0& -0.5263& 51.5789& 0\end{array}\right],B=\left[\begin{array}{c}0\\ 1.7895\\ 0\\ 5.2632\end{array}\right]\end{array}$$

系统的特征方程$det(\lambda I-A)=0$，求解得到特征根同样为[-7.22，-0.1，0，7.14]，系统不稳定。
能控性和能观性判据
$$\begin{array}{c}rank\left[\begin{array}{ccc}B& AB& A^{2}B\cdots A^{n-1}B\end{array}\right]=4\\ rank\left[\begin{array}{ccc}C& CA& C{A}^2\cdots C{A}^{n-1}\end{array}\right]=4\end{array}$$

所以直线一级倒立摆系统是能控的和能观测的。

由传递函数建立系统开环模型
输入为阶跃函数
$$e(t)=\{\begin{array}{c}0,t<0\\ 1,t>0\end{array}$$
拉普拉斯变换
$$U(s)={\int }_0^{\infty }e(t)e^{-st}\mathrm{d}\mathrm{t}={\int }_0^{\infty }{\mathrm{e}}^{-\mathrm{s}\mathrm{t}}\mathrm{d}\mathrm{t}=-\frac{{\mathrm{e}}^{-\mathrm{s}\mathrm{t}}}{\mathrm{s}}{|}_0^{\infty }=\frac{1}{\mathrm{s}}$$

输出
$$\Theta (s)=G(s)U(s)=\frac{-0.15s^2}{s(s+7.22)(s+0.1)(s-7.14)}$$
逆拉普拉斯变换
$$\begin{gathered} \theta (t)=L^{-1}[\Theta (s)]=L^{-1}[\frac{-0.15s^2}{s(s+7.22)(s+0.1)(s-7.14)}] \\ =L^{-1}[\frac{0.0103}{s+7.22}+\frac{-0.0106}{s+0.1}+\frac{0.0003}{s-7.14}] \\ =0.0103e^{-7.22t}-0.0106e^{-0.1t}+0.0003e^{7.14t} \end{gathered}$$
利用matlab编写以上函数，带入时间t=0:0.001:10就可以得到响应的曲线如下（此处也可以直接用matlab自带的函数impulse计算单位脉冲响应）

simulink的仿真模型如下图，这里输入是阶跃函数，模型以传递函数的形式给出

simulin仿真结果如下图，基本趋势和matlab的结果一致。

以上响应的结果都可以看出该开环模型的输出是明显发散的，说明模型不稳定，需要采用控制算法对其进行调控。

3.极点配置法

经典控制理论中，闭环传递函数的极点影响着系统运动的模态，同时极点的分布也影响着运动的瞬态性能，所以理想的办法是根据预期的性能设定相应的指标，求解极点的分布。利用根轨迹校正法，在开环系统中增设零点使整个根轨迹向左移动，从而增加系统的相对稳定性，减少系统的调节时间。

而在现代控制理论中，改变极点的分布称之为极点配置，可以通过选择反馈增益矩阵，将闭环系统的极点恰好配置在根平面上所期望的位置，以获得所希望的动态性能。将系统由不稳定变为稳定的过程也称之为“镇定”。

线性定常系统状态空间模型为：
$$\{\begin{array}{c}\dot{X}=AX+BU\\ Y=CX+DU\end{array}$$

若将状态作为反馈变量形成负反馈，可记$U=-KX$。其中$K$为状态反馈增益矩阵。得到状态反馈后的系统状态空间模型：
$$\begin{array}{c}\dot{X}=(A-BK)X\end{array}$$

系统特征式为$det(sI-A+BK)={\alpha }_n(s-{\lambda }_1^{\ast })(s-{\lambda }_2^{\ast })\cdots (s-{\lambda }_n^{\ast })$。其中， ${\lambda }_i^{\ast }$为期望的闭环极点。通过将由预期的极点计算得到的反馈矩阵作用到系统上，就可以将闭环系统调整为稳定的系统。

极点配置法的关键就在于期望极点的位置选取。对于一个$n$维系统，就需要给定$n$个实极点。要考虑极点对于系统的主导影响作用以及系统零点分布的状况，同时还需考虑系统抗干扰的能力。

求解反馈矩阵$K$的过程：
(1）给定的线性定常系统和一组期望的闭环极点$p_{need}=[{\lambda }_1,{\lambda }_2,...,{\lambda }_n]$，计算得到反馈矩阵的步骤如下：
(2）检验系统的能控性。如果系统是能控的，则继续第二步。
$$\begin{array}{c}rank(Q_c)=n\\ Q_c=\left[\begin{array}{ccc}B& AB& A^{2}B\cdots A^{n-1}B\end{array}\right]\end{array}$$

单输入系统的能控标准型
$$\{\begin{array}{c}\dot{X}=AX+BU\\ Y=CX\end{array}$$

构造一能满足条件的可逆变换矩阵$T_1$如下所示：
$$\begin{array}{c}{T}_1=\left(A^{n-1}B,A^{n-2}B,\dots ,AB,B\right)\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ a_{n-1}& 1& 0& 0& 0\\ ⋮& ⋮& \ddots & 0& 0\\ a_2& a_3& \dots & 1& 0\\ a_1& a_2& \dots & a_{n-1}& 1\end{array}\right)\end{array}$$

则可得到能控标准型下的系统变量坐标 $X=T_1\bar{X}$，$\dot{X}=T_1\dot{\bar{X}}$。
$$\begin{array}{c}\dot{\bar{X}}=T_1^{-1}A{T}_1\bar{X}+T_1^{-1}BU=\bar{A}\bar{X}+\bar{B}U\end{array}$$

其中
$$\begin{array}{c}\bar{A}=T_1^{-1}A{T}_1=\left[\begin{array}{cccc}0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& 1\\ -a_0& -a_1& \cdots & -a_{n-1}\end{array}\right]\\ \bar{B}=T_1^{-1}BU={\left[\begin{array}{cccc}0& \cdots & 0& 1\end{array}\right]}^T\end{array}$$

(3）系统矩阵$\bar{A}$的特征多项式
$$\begin{array}{c}\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I-\bar{A})={\lambda }^n+a_{n-1}{\lambda }^{n-1}+...+a_1\lambda +a_0\end{array}$$

确实系数$a_0，a_1，...，a_{n-1}$的值。
(4）利用给定的期望闭环极点计算期望的闭环特征多项式：
$$\begin{array}{c}(\lambda -{\lambda }_1)(\lambda -{\lambda }_2)...(\lambda -{\lambda }_n)={\lambda }^n+b_{n-1}{\lambda }^{n-1}+...+b_1\lambda +b_0\end{array}$$

确实系数$b_0，b_1，...，b_{n-1}$的值。
$$\begin{array}{c}\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I-(\bar{A}-\bar{B}K))\\ =\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I-(\left[\begin{array}{cccc}0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\\ -a_0& -a_1& \cdots & -a_{n-1}\end{array}\right]-\left[\begin{array}{c}0\\ ⋮\\ 0\\ 1\end{array}\right].\left[\begin{array}{cccc}{k}_1& \cdots & k_{n-1}& k_n\end{array}\right]))\\ =\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I-(\left[\begin{array}{cccc}0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\\ -a_0& -a_1& \cdots & -a_{n-1}\end{array}\right]-\left[\begin{array}{cccc}0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 0\\ k_1& k_2& \cdots & k_n\end{array}\right]))\\ =\mathrm{d}\mathrm{e}\mathrm{t}(\lambda I-(\left[\begin{array}{cccc}0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\\ -a_0-k_1& -a_1-k_2& \cdots & -a_{n-1}{k}_n\end{array}\right]))\\ ={\lambda }^n+(a_{n-1}+k_n){\lambda }^{n-1}+...+(a_1+k_{n-1})\lambda +(a_0+k_1)\end{array}$$

(5）确定极点配置状态反馈增益矩阵：
由
$$\begin{array}{c}{\lambda }^n+b_{n-1}{\lambda }^{n-1}+...+b_1\lambda +b_0=\\ {\lambda }^n+(a_{n-1}+k_n){\lambda }^{n-1}+...+(a_1+k_{n-1})\lambda +(a_0+k_1)\end{array}$$

得到$k_i=b_{i-1}-a_{i-1}，i=1:n$。进而求得反馈矩阵$K$如下：
$$\begin{array}{c}\mathbf{K}=\left[\begin{array}{lllll}{b}_0-a_0& b_1-a_1& \cdots & b_{n-2}-a_{n-2}& b_{n-1}-a_{n-1}\end{array}\right]\end{array}$$

#matlab代码

clear;clc;close all;
%% 基本参数
M = 0.5;%%小车质量
m = 0.5;%%倒立摆的质量
miu = 0.1;%%地面摩擦系数
I = 0.006;%%惯性矩
L = 0.3;%%长度
g = 9.8;%%加速度
%% 状态方程矩阵
P = (M+m)*I+M*m*L^2;%%状态方程的分母
A = [0 1 0 0;
    0 -miu*(m*L^2+I)/P m^2*g*L^2/P 0;
    0 0 0 1;
    0 -miu*m*L/P (M+m)*m*g*L/P 0];
B = [0;(I+m*L^2)/P;0;m*L/P];
C = [1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
D = [0;0;0;0];
%% 极点配置法
p_ex = eig(A)';%%%A矩阵特征值求解,系统极点
p_need = [-10,-7,-1.901,-1.9];%%极点配置,将系统极点调到复平面，将得到稳定的系统
K1 = place(A,B,p_need);%%AB为系统的状态空间矩阵，向量P中是期望的闭环极点位置，返回值是增益向量。
A1 = A-B*K1;%%极点配置之后的矩阵
p_new = eig(A-B*K1)';%%极点逆向求解，极点配置之后的系统极点（验证极点配置成功与否）
t = 0:0.01:4;
x0 = [0;0;0.2;0];%%初始值
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%零输入响应
sys_ex = ss(A,B,C,D);%%创建连续的状态空间模型
y_ex = initial(sys_ex,x0,t);%%零输入响应,sys为传递函数模型，x0为初始状态，t为指定的响应时间。
sys_new = ss(A-B*K1,B,C,D);%%创建连续的状态空间模型
y_new = initial(sys_new,x0,t);%%零输入响应,sys为传递函数模型，x0为初始状态，t为指定的响应时间。

figure('name','零输入响应 极点配置法')
subplot(211)
plot(t,y_ex(:,1)),hold on
plot(t,y_ex(:,2)),hold on
plot(t,y_ex(:,3)),hold on
plot(t,y_ex(:,4)),hold on
xlabel('t(s)')
ylabel('响应')
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');
title('极点配置前')

subplot(212)
plot(t,y_new(:,1)),hold on
plot(t,y_new(:,2)),hold on
plot(t,y_new(:,3)),hold on
plot(t,y_new(:,4)),hold on
xlabel('t(s)')
ylabel('响应')
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');
title('极点配置后')

%%%%%%%%%simulink 零输入响应
[t_sim,y_sim] = sim('pendulum_initial_simulink.mdl');
figure('name','simulink 控制后系统零输入响应')
plot(t_sim,y_sim(:,1)),hold on
plot(t_sim,y_sim(:,2)),hold on
plot(t_sim,y_sim(:,3)),hold on
plot(t_sim,y_sim(:,4)),hold on
xlabel('t(s)')
ylabel('响应')
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%阶跃响应
y_ex_step = step(A,B,C,D);%%%step计算一个系统的阶跃响应
y_new_step = step(A1,B,C,D);%%%step计算一个系统的阶跃响应

figure('name','阶跃响应 极点配置法')
subplot(211)
plot(y_ex_step(:,1)),hold on
plot(y_ex_step(:,2)),hold on
plot(y_ex_step(:,3)),hold on
plot(y_ex_step(:,4)),hold on
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');
title('极点配置前')

subplot(212)
plot(y_new_step(:,1)),hold on
plot(y_new_step(:,2)),hold on
plot(y_new_step(:,3)),hold on
plot(y_new_step(:,4)),hold on
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');
title('极点配置后')

%%%%%%%%%simulink 阶跃响应
[t_sim,y_sim] = sim('pendulum_step_simulink.mdl');
figure('name','simulink系统阶跃响应')
plot(t_sim,y_sim(:,1)),hold on
plot(t_sim,y_sim(:,2)),hold on
plot(t_sim,y_sim(:,3)),hold on
plot(t_sim,y_sim(:,4)),hold on
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');

零输入条件计算得到的系统响应曲线，初始扰动给摆杆一角度$0.2$rad，上图为极点配置前的4个自由度响应曲线，明显发散，下图为极点配置之后的结果图，4条曲线基本都趋于稳定，且随着时间增加趋于零。系统大约在3s左右趋于稳定。
结合simulink仿真验证该结果：

给一阶跃扰动，初始状态都设置为0，极点配置之后的结果如下所示：

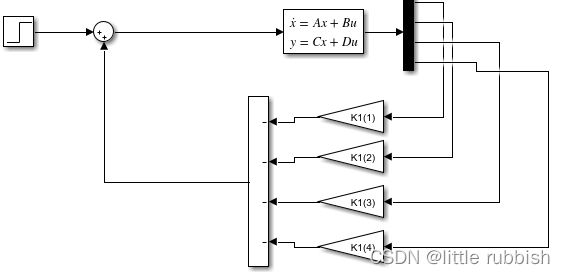
可以看到，matlab仿真结果和simulink的结果曲线完全一致，说明建立的模型是正确的。但是也能发现当前极点配置法得到的系统响应曲线超调量过大，原因在于极点配置法是对系统控制量$X$乘以一个反馈系数$K$，类似于比例控制，将使稳定系统产生较大的超调量，且没办法消除。因此后续分许需要考虑结合其他控制方法进行调控。后续仅分析零输入响应。

期望极点 [-10,-7,-19.01,-1.9]

期望极点 [-100,-7,-19.01,-19]

以上两图发现，期望系统极点越小，系统响应速度越快，达到稳定的时间越短，但是系统的超调量会也会快速增大。

4.LQR控制

4.1.基本原理

最优控制，其本质就是让系统以某种最小的代价来运行，当这个代价被定义为二次泛函且系统是线性时，这个问题就称为线性二次问题，设计的控制器（即问题的解）可以称为LQR（Linear Quadratic Regulator）线性二次调节器。LQR通过取全状态反馈，将不同状态加权和得到最优控制量。
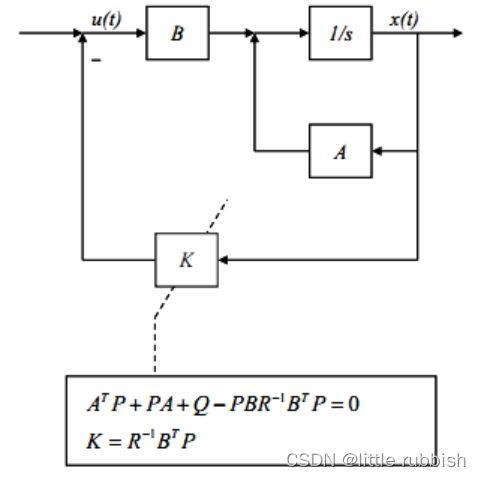
LQR控制结构原理框图：（参考https://blog.csdn.net/ChenGuiGan/article/details/116483597）

LQR控制器设计步骤：
1.根据我们想要的期望状态，初步设计好$Q$（状态权重矩阵），$R$（控制权重矩阵），以及目标方程$J$。
一方面我们希望系统达到稳定状态，及偏差最小，状态量$X$最小; 另一方面我们希望控制量$U$较小，即付出较小的代价达到我们的目的。最优控制目标方程：
$$\begin{array}{c}J=\mathrm{m}\mathrm{i}\mathrm{n}{\int }_0^{\infty }\left(X^{T}QX+U^{T}RU\right)dt=\mathrm{m}\mathrm{i}\mathrm{n}{\int }_0^{\infty }\left(X^T(Q+K^{T}RK)X\right)dt\end{array}$$

其中$U=-KX$，$Q$为半正定对称阵，$R$为正定对称阵（一般都取对角阵）。且系统完全能控，完全能观，控制量$u$不受约束。因为状态量$X$和控制量$U$中取值有正有负，所以需要平方和最小，在矩阵中没有平方，因此这里目标函数采用了转置乘以本身的做法模拟矩阵的平方 。其实我们可以把$X^{T}AX$看作是$a{x}^2$的多维扩展表达式，这里我们需要$Q$为半正定，就是希望$Q$能起到$a\ge 0$的效果，同样$R$为正定矩阵也是希望矩阵$R$能够起到$a>0$的效果。

$Q$为我们提前标定的对角矩阵，标定值对应状态量$X$各个参数的权重，也可以为非对角矩阵，考虑不同参数之间的相互关系。同样的$R$也为对应控制量$U$的对角矩阵，也可以考虑相互关系。

$Q$选取较大的值，为了目标函数$J$较小，状态量$X$也应该较小，也就是意味着闭环系统的矩阵$(A-BK)$的特征值处于S平面左边更远的地方，这样状态就以更快的速度衰减到0；加大$R$的值，会使得对应的控制量$U$减小，控制器执行更少的动作，意味着系统的状态衰减将变慢。所以要综合看具体的实际应用场景来调节，鱼和熊掌不可兼得。建议在不同场景下采用不同的参数。

2.由目标方程$J$推导Riccati方程求解矩阵$P$。
为了找到$K$，先假设存在一个常量矩阵$P$使得：
$$\begin{array}{c}\frac{d}{dt}(X^{T}PX)=-X^T(Q+K^{T}RK)X\\ J=-{\int }_0^{\infty }\frac{d}{dt}(X^{T}PX)dt=X^T(0)PX(0)\end{array}$$

这里假设了闭环系统是稳定的，所以$t$趋于$\infty$时，$X(t)$趋于0。
上面微分方程展开可以得到
$$\begin{array}{c}\frac{d}{dt}(X^{T}PX)=-X^T(Q+K^{T}RK)X\\ {\dot{X}}^{T}PX+X^{T}P\dot{X}=-X^{T}QX-X^T{K}^{T}RKX\\ {\dot{X}}^{T}PX+X^{T}P\dot{X}+X^{T}QX+X^T{K}^{T}RKX=0\end{array}$$

将$\dot{X}=(A-BK)X=A_{t}X$带入上式可以得到
$$\begin{array}{c}{X}^T{A}_t^{T}PX+X^{T}P{A}_{t}X+X^{T}QX+X^T{K}^{T}RKX=0\\ X^T(A_t^{T}P+P{A}_t+Q+K^{T}RK)X=0\end{array}$$

这个式子要成立的话，括号里面的项必须等于0。
$$\begin{array}{c}{A}_t^{T}P+P{A}_t+Q+K^{T}RK=0\\ (A-BK{)}^{T}P+P(A-BK)+Q+K^{T}RK=0\\ A^{T}P+PA+Q+K^{T}RK-K^T{B}^{T}P-PBK=0\end{array}$$

这是一个关于$K$的二次型等式，当然这个二次型是我们不愿看到的，因为计算复杂。现在只要这个等式成立，我们何必不选择$K$使得两个二次项正好约掉了呢？这样既符合了要求，又简化了计算。取$K=R^{-1}{B}^{T}P$，带入上式就可以得到：
$$\begin{array}{c}{A}^{T}P+PA+Q+(R^{-1}{B}^{T}P{)}^{T}R(R^{-1}{B}^{T}P)-(R^{-1}{B}^{T}P{)}^T{B}^{T}P-PB{R}^{-1}{B}^{T}P=0\\ A^{T}P+PA+Q+P^{T}B{R}^{-1}R{R}^{-1}{B}^{T}P-P^{T}B{R}^{-1}{B}^{T}P-PB{R}^{-1}{B}^{T}P=0\\ A^{T}P+PA+Q+P^{T}B{R}^{-1}(R{R}^{-1}-1)B^{T}P-PB{R}^{-1}{B}^{T}P=0\\ A^{T}P+PA+Q-PB{R}^{-1}{B}^{T}P=0\end{array}$$

可以发现$K$的二次项没有了，可$K$的取值和$P$有关，而$P$是我们假设的一个量，$P$只要使得的上式成立就行了。而上式在现代控制理论中极其重要，它就是有名的Riccati 方程。
$$\begin{array}{c}{A}^{T}P+PA+Q-PB{R}^{-1}{B}^{T}P=0\end{array}$$

注意到该式中$A、B、Q、R$都是已知的，求解上式就可以得到$P$矩阵的表达式。
3.当求解得到$P$矩阵后，由公式取$K=R^{-1}{B}^{T}P$计算得到反馈矩阵$K$的表达式，进而就可以进行LQR的反馈控制$U=-KX$。

4.2.与全状态反馈极点配置（Pole placement）方法的异同

在控制结构上两者是完全相同的，都是通过将全状态加权后反馈得到控制量，完成控制任务。不同点是极点配置设计方法是通过状态反馈，将被控对象的特征极点配置到理想平面的理想位置，如果有参考稳态误差，加上一个比例调节项来消除，从而达到想要的控制效果。从状态空间方程的角度来看，原来的被控对象状态矩阵是A阵，特征值和特征向量已经确定，通过全状态反馈后，被控对象成为A-BK，调节K可以达到调节系统的目的。补充一点，极点配置法的前提是系统能控能观测。

LQR在结构上是一样的，但是整个设计的思路是完全不同的，LQR通过构造了误差状态量和控制量的二次型性能代价函数，通过调节惩罚的力度来达到想要的控制效果，相对来说LQR方法调节起来更加直观，设计师对于状态量误差的容惩罚度（Q）还是对于执行器的付出的惩罚度（R）决定了最终的设计的最优控制量。

%% LQR控制（和极点配置法类似）
Q=[100 0 0 0;%%小车位置的误差代价
    0 2 0 0;%%小车速度的误差代价
    0 0 3 0;%%摆杆转角的误差代价
    0 0 0 1];%%摆杆转角速度的误差代价   %%一般是对角阵
R=0.01;%%输入误差代价，减小时超调量增大，但是系统会更快趋于0
K=lqr(A,B,Q,R);
sys=ss(A-B*K,B,C,D);%经过状态量反馈后的新状态矩阵
y_LQR = initial(sys,x0,t);

figure('name','LQR控制 系统零输入响应')
set(gcf,'Position',[100 100 400 150]);%%x轴长度，y轴长度，图像长度，图像高度
plot(t,y_LQR(:,1)),hold on
plot(t,y_LQR(:,2)),hold on
plot(t,y_LQR(:,3)),hold on
plot(t,y_LQR(:,4)),hold on
set(gca,'Position',[0.1 0.23 0.88 0.74]);%%x轴长度，y轴长度，图像长度，图像高度
xlabel('t/s');
ylabel('响应');
gca1 = legend('X car','V car','\theta rod','\alpha rod');
set(gca1,'location','best');

Q=[1 0 0 0;0 2 0 0;0 0 3 0;0 0 0 1];R=0.01；

Q=[100 0 0 0;0 2 0 0;0 0 3 0;0 0 0 1];R=0.01；

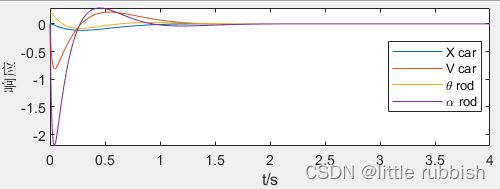
增大$Q$，为获得较小的目标函数，观测量将更小，系统更快的达到稳定状态。
Q=[1 0 0 0;0 2 0 0;0 0 3 0;0 0 0 1];R=1；

增大$R$，为获得较小的目标函数，控制量将更小，控制器变化缓慢，系统响应不容易出现超调的现象，但是达到稳定状态的速度也更慢。

---

总结：

此文档为本人初步采用一级倒立摆学习控制和simulink时的记录，仅用于个人学习。文档中含有大量网上摘抄的内容，少部分注释了来源，如有冒犯请谅解。
本文中仅采用了极点配置法和LQR来对倒立摆的稳定进行控制，两种方法仅在获取反馈矩阵的途径上有所不同，本质上都是给系统的观测量加一个比例反馈系数以调控其稳定性，在计算过程中发现由于仅有比例控制带来的超调量过大的问题尤其明显，因此后续还希望学习更多的控制方法以克服该问题。另外极点配置法需要给定预期的极点位置，LQR需要先给定观测量和控制量的权重矩阵$Q、R$，这两个矩阵的选取也需要根据一定的经验以及具体问题具体分析。