【吴恩达深度学习笔记】1.3 浅层神经网络Shallow neural networks
第一门课 神经网络和深度学习(Neural Networks and Deep Learning)
3.1神经网络概述(Neural Network Overview)
感觉这块没啥好记的
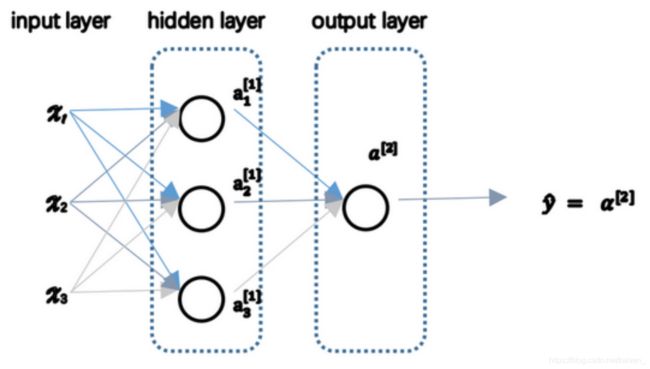
3.2 神经网络的表示(Neural Network Representation)
神经网络包括
- 输入层(input layer):包含输入特征 x 1 , x 2 , . . . x_1,x_2,... x1,x2,...
- 隐藏层(hidden layer):训练数据
- 输出层(output layer):产生预测值 y 1 , y 2 , . . . y_1,y_2,... y1,y2,...
将输入层的激活值记为 a [ 0 ] a^{[0]} a[0],隐藏层的激活值记为 a [ 1 ] a^{[1]} a[1],第一个结点记为 a 1 [ 1 ] a^{[1]}_{1} a1[1],第二个结点记为 a 2 [ 1 ] a^{[1]}_{2} a2[1],以此类推,输出层的 y ^ \hat y y^取 a [ 2 ] a^{[2]} a[2]。
3.3 计算一个神经网络的输出(Computing a Neural Network’s output)
给定一个只有一个隐藏层的两层神经网络结构, x x x表示输入特征, a a a表示每个神经元的输出, W W W表示特征的权重,上标表示神经网络的层数(隐藏层为1),小标表示该层的第几个神经元。
神经网络的计算

隐藏层节点单元的计算:
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z^{[1]}_1=w^{[1]T}_1x+b^{[1]}_1,a^{[1]}_1=\sigma(z^{[1]}_1) z1[1]=w1[1]Tx+b1[1],a1[1]=σ(z1[1])
z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 2 [ 1 ] = σ ( z 2 [ 1 ] ) z^{[1]}_2=w^{[1]T}_2x+b^{[1]}_2,a^{[1]}_2=\sigma(z^{[1]}_2) z2[1]=w2[1]Tx+b2[1],a2[1]=σ(z2[1])
z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 1 ] , a 3 [ 1 ] = σ ( z 3 [ 1 ] ) z^{[1]}_3=w^{[1]T}_3x+b^{[1]}_3,a^{[1]}_3=\sigma(z^{[1]}_3) z3[1]=w3[1]Tx+b3[1],a3[1]=σ(z3[1])
z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 4 [ 1 ] = σ ( z 4 [ 1 ] ) z^{[1]}_4=w^{[1]T}_4x+b^{[1]}_4,a^{[1]}_4=\sigma(z^{[1]}_4) z4[1]=w4[1]Tx+b4[1],a4[1]=σ(z4[1])
向量化计算
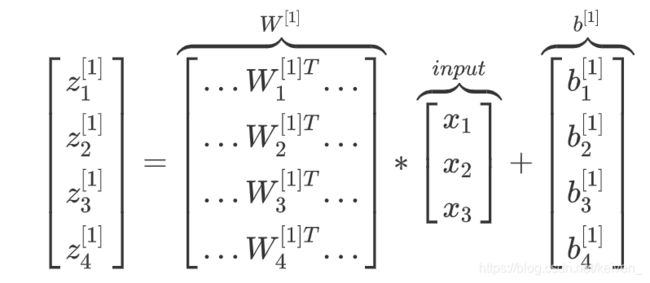
z [ n ] = w [ n ] x + b [ n ] z^{[n]}=w^{[n]}x+b^{[n]} z[n]=w[n]x+b[n]
其中 w w w是一个4X3的矩阵
3.4 多样本向量化(Vectorizing across multiple examples)
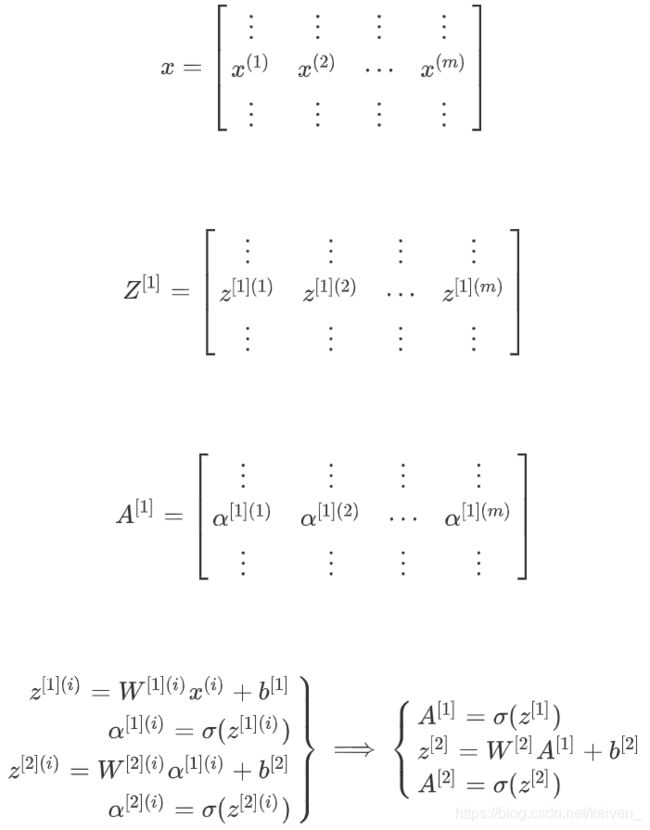
a [ 2 ] ( i ) a^{[2](i)} a[2](i)中 [ 2 ] [2] [2]指神经网络的第二层, ( 2 ) (2) (2)指第 i i i个训练样本。
对于矩阵 A , Z , X A,Z,X A,Z,X,水平方向上代表了各个训练样本,竖直方向上对应不同的输入特征,即不同的索引对应于不同的隐藏单元。
3.5 向量化实现的解释(Justification for vectorized implementation)
对单个样本的计算 z [ 1 ] ( i ) = W [ 1 ] x [ i ] + b [ 1 ] z^{[1](i)}=W^{[1]}x^{[i]}+b^{[1]} z[1](i)=W[1]x[i]+b[1],当有不同的训练样本时,将其堆到矩阵 X X X的各列中。
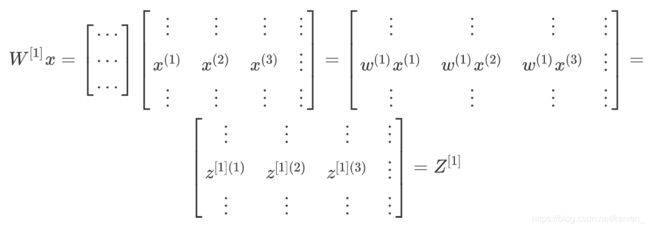
3.6 激活函数(Activation functions)
在神经网络的前向传播中的 a [ 1 ] = σ ( z [ 1 ] ) a^{[1]}=\sigma (z^{[1]}) a[1]=σ(z[1])使用到了sigmoid函数,sigmoid函数在这里被称为激活函数: a = σ ( z ) = 1 1 + e − z a=\sigma (z)=\frac{1}{1+e^{-z}} a=σ(z)=1+e−z1
通常情况下我们使用不同的非线性函数 g ( z ) g(z) g(z),tanh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。
a = t a n h ( z ) = e z − e − z e z + e − z a=tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} a=tanh(z)=ez+e−zez−e−z
tanh函数的值域在-1到1之间,数据的平均值接近0而不是0.5,这会使下一层的学习更加简单。sigmoid函数和tanh函数共同的缺点:在z特别大或特别小时导数的梯度或者函数的斜率接近于0,导致降低梯度下降的速度降低。
在机器学习中有一个很流行的函数:修正线性单元函数(ReLu),在z是正数时导数恒等于1,在z是负数时,导数恒等于0。
a = R e L u ( z ) = m a x ( 0 , z ) a=ReLu(z)=max(0,z) a=ReLu(z)=max(0,z)
激活函数选择的经验法则:
- 若输出是0、1值(二分类问题),则输出层选择sigmoid函数,其余所有单元选择ReLu函数
- 若隐藏层不确定使用哪个激活函数,通常选择ReLu函数
还有另一版本的ReLu函数Leaky ReLu,当z是负值时函数值不为0,而是微微倾斜,这个函数的激活效果优于ReLu,尽管使用不多。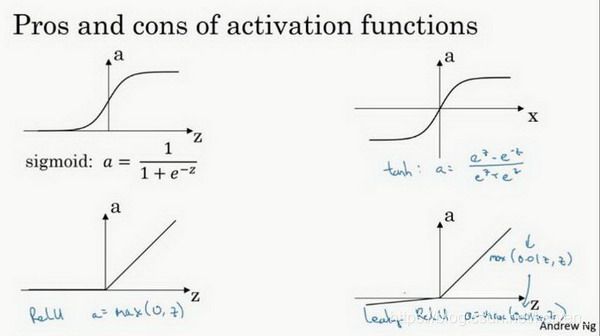
3.7 为什么需要非线性激活函数?(Why need a nonlinear activation function?)
如果你是用线性激活函数或者叫恒等激励函数,那么神经网络只是把输入线性组合再输出。不能在隐藏层用线性激活函数,可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数,唯一可以用线性激活函数的通常就是输出层。
3.8 激活函数的导数(Derivatives of activation functions)
1.Sigmoid activation function
d d z g ( z ) = d d z g ( 1 1 + e − z ) = 1 1 + e − z ( 1 − 1 1 + e − z ) = g ( z ) ( 1 − g ( z ) ) \frac{d}{dz}g(z)=\frac{d}{dz}g(\frac{1}{1+e^{-z}})=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})=g(z)(1-g(z)) dzdg(z)=dzdg(1+e−z1)=1+e−z1(1−1+e−z1)=g(z)(1−g(z))
当 z = ± 10 z=±10 z=±10时, g ( z ) ′ ≈ 0 g(z)'≈0 g(z)′≈0
当 z = 0 z=0 z=0时, g ( z ) ′ = 1 4 g(z)'=\frac{1}{4} g(z)′=41
在神经网络中, a = g ( z ) , g ( z ) ′ = a ( 1 − a ) a=g(z),g(z)'=a(1-a) a=g(z),g(z)′=a(1−a)
2.Tanh activation function
d d z g ( z ) = d d z g ( e z − e − z e z + e − z ) = 1 − ( t a n h ( z ) ) 2 \frac{d}{dz}g(z)=\frac{d}{dz}g(\frac{e^z-e^{-z}}{e^z+e^{-z}})=1-(tanh(z))^2 dzdg(z)=dzdg(ez+e−zez−e−z)=1−(tanh(z))2
当 z = ± 10 z=±10 z=±10时, g ( z ) ′ ≈ 0 g(z)'≈0 g(z)′≈0
当 z = 0 z=0 z=0时, g ( z ) ′ = 0 g(z)'=0 g(z)′=0
在神经网络中, a = g ( z ) , g ( z ) ′ = 1 − a 2 a=g(z),g(z)'=1-a^2 a=g(z),g(z)′=1−a2
3.Rectified linear unit(ReLu)
g ( z ) = m a x ( 0 , z ) g(z)=max(0,z) g(z)=max(0,z)
g ( z ) ′ = { 0 i f z < 0 1 i f z > 0 u n d e f i n e d i f z = 0 g(z)'=\left\{\begin{matrix} 0 & if\space z<0\\ 1 & if\space z>0\\ undefined & if\space z=0 \end{matrix}\right. g(z)′=⎩⎨⎧01undefinedif z<0if z>0if z=0
通常在 z = 0 z=0 z=0时给定其导数1,0;当然 z = 0 z=0 z=0的情况很少。
4.Leaky Rectified linear unit(Leaky ReLu)
g ( z ) = m a x ( 0.01 z , z ) g(z)=max(0.01z,z) g(z)=max(0.01z,z)
g ( z ) ′ = { 0.01 i f z < 0 1 i f z > 0 u n d e f i n e d i f z = 0 g(z)'=\left\{\begin{matrix} 0.01 & if\space z<0\\ 1 & if\space z>0\\ undefined & if\space z=0 \end{matrix}\right. g(z)′=⎩⎨⎧0.011undefinedif z<0if z>0if z=0
通常在 z = 0 z=0 z=0时给定其导数1,0.01;当然 z = 0 z=0 z=0的情况很少。
3.9 神经网络的梯度下降(Gradient descent for neural networks)
给定一单层神经网络,包括参数 W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1], W [ 2 ] W^{[2]} W[2], b 2 ] b^{2]} b2], n x n_x nx代表输入特征的个数, n [ 1 ] n^{[1]} n[1]表示隐藏层单元个数, n [ 2 ] n^{[2]} n[2]表示输出层单元个数。
矩阵 W [ 1 ] W^{[1]} W[1]维度为 ( n [ 1 ] , n [ 0 ] ) (n^{[1]},n^{[0]}) (n[1],n[0]),矩阵 b [ 1 ] b^{[1]} b[1]维度为 ( n [ 1 ] , 1 ) (n^{[1]},1) (n[1],1),矩阵 W [ 2 ] W^{[2]} W[2]维度为 ( n [ 2 ] , n [ 1 ] ) (n^{[2]},n^{[1]}) (n[2],n[1]),矩阵 b [ 2 ] b^{[2]} b[2]维度为 ( n [ 2 ] , 1 ) (n^{[2]},1) (n[2],1)。 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]的维度均为 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m)。
训练参数需要做梯度下降,在训练神经网络时,要随机初始化参数,而不是初始化为全零。
forword propagation:
z [ 1 ] = W [ 1 ] x + b [ 1 ] a [ 1 ] = σ ( z [ 1 ] ) z^{[1]}=W^{[1]}x+b^{[1]}\space \space \space a^{[1]}=\sigma(z^{[1]}) z[1]=W[1]x+b[1] a[1]=σ(z[1])
z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] a [ 2 ] = g [ 2 ] ( z [ 2 ] ) = σ ( z [ 2 ] ) z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\space \space \space a^{[2]}=g^{[2]}(z^{[2]})=\sigma(z^{[2]}) z[2]=W[2]a[1]+b[2] a[2]=g[2](z[2])=σ(z[2])
back propagation:
d z [ 2 ] = A [ 2 ] − Y , Y = [ y [ 1 ] y [ 2 ] . . . y [ m ] ] dz^{[2]}=A^{[2]}-Y,Y=[y^{[1]}\space y^{[2]}\space ...\space y^{[m]}] dz[2]=A[2]−Y,Y=[y[1] y[2] ... y[m]]
d W [ 2 ] = 1 m d z [ 2 ] A [ 1 ] T dW^{[2]}=\frac{1}{m}dz^{[2]}A^{[1]T} dW[2]=m1dz[2]A[1]T
d b [ 2 ] = 1 m n p . s u m ( d z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[2]}=\frac{1}{m}np.sum(dz^{[2]},axis=1,keepdims=True) db[2]=m1np.sum(dz[2],axis=1,keepdims=True)
d z [ 1 ] = W [ 2 ] T d z [ 2 ] ∗ g [ 1 ] ′ ( z [ 1 ] ) dz^{[1]}=W^{[2]T}dz^{[2]}*g^{[1]'}(z^{[1]}) dz[1]=W[2]Tdz[2]∗g[1]′(z[1])
d W [ 1 ] = 1 m d z [ 1 ] x T dW^{[1]}=\frac{1}{m}dz^{[1]}x^{T} dW[1]=m1dz[1]xT
d b [ 1 ] = 1 m n p . s u m ( d z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) db^{[1]}=\frac{1}{m}np.sum(dz^{[1]},axis=1,keepdims=True) db[1]=m1np.sum(dz[1],axis=1,keepdims=True)
其中axis=1在python中表示水平相加求和,keepdims确保矩阵 d b [ 2 ] db^{[2]} db[2]这个向量输出的维度为 ( n , 1 ) (n,1) (n,1)这样的标准形式。
3.10(选修)直观理解反向传播(Backpropagation intuition)
3.11 随机初始化(Random Initialization)
如果在神经网络中将权重或者参数初始化为0,那么梯度下降将不起作用。
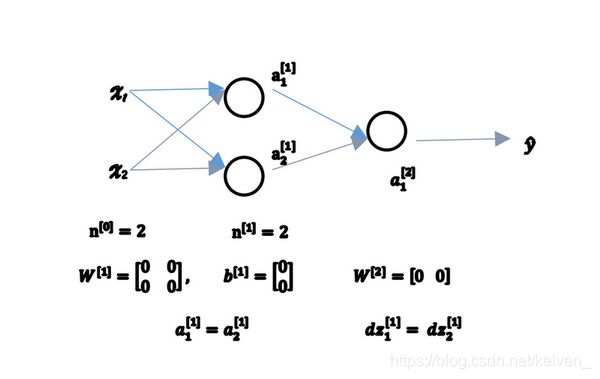
实际中应该把 W [ 1 ] W^{[1]} W[1]设为np.random.randn(2,2)(生成高斯分布),通常再乘一个很小的数,如0.01,这样把它初始化为很小的随机数。 b b b没有对称问题,可以将其初始化为0。只要随机初始化 W W W就有不同的隐含单元计算不同的东西,就不会存在symmetry breaking problem,相似的 W [ 2 ] W^{[2]} W[2]也是如此。
W [ 1 ] = n p . r a n d o m . r a n d n ( 2 , 2 ) ∗ 0.01 , b [ 1 ] = n p . z e r o s ( ( 2 , 1 ) ) W^{[1]}=np.random.randn(2,2)*0.01,b^{[1]}=np.zeros((2,1)) W[1]=np.random.randn(2,2)∗0.01,b[1]=np.zeros((2,1))
W [ 2 ] = n p . r a n d o m . r a n d n ( 2 , 2 ) ∗ 0.01 , b [ 2 ] = 0 W^{[2]}=np.random.randn(2,2)*0.01,b^{[2]}=0 W[2]=np.random.randn(2,2)∗0.01,b[2]=0
乘0.01而不是100或者1000是因为如果使用sigmoid/tanh为激活函数,初始化值很大的时候 z z z会很大或者很小,梯度下降会很慢,学习速度就会很慢。
错题笔记
Logistic Regression doesn’t have a hidden layer. If you initialize the weights to zeros, the first example x fed in the logistic regression will output zero but the derivatives of the Logistic Regression depend on the input x (because there’s no hidden layer) which is not zero. So at the second iteration, the weights values follow x’s distribution and are different from each other if x is not a constant vector.
Logistic回归没有隐藏层。 如果将权重初始化为零,则Logistic回归中的第一个示例x将输出零,但Logistic回归的导数取决于不是零的输入x(因为没有隐藏层)。 因此,在第二次迭代中,如果x不是常量向量,则权值遵循x的分布并且彼此不同。
