abaqus 不收敛问题
背景介绍
有限元分析的过程主要包括复杂模型建立、网格划分、材料赋予、边界条件设立以及外载荷添加等,在完成有限元模拟前处理过程后提交任务进行计算,有的时候会出现不收敛问题,常常让人很头大,这个时候应该如何来解决呢?
解决办法
不收敛的种类:(1)提交任务后第一步就开始就出现不收敛问题,一般情况下是有限元模拟前处理过程中存在部分问题,这种不收敛性比较好解决,可能的原因有:边界条件问题(约束不足、接触属性定义相关问题等)以及材料参数设置问题(在材料属性以及相关参数定义时单位没有统一,引起初始荷载过大等问题);(2)随着载荷步增量的不断增加,在中途出现不收敛问题,这一部分就需要根据已有的计算结果和模型进行判断,根据以往的相关经验,采用有限元方法模拟试件断裂、材料软化、屈曲以及颈缩等问题时容易出现此种不收敛问题,一般情况下,单元网格划分方法、单元选择以及材料相关参数选用都对收敛性具有影响,有的时候需要引入相应的阻尼使得模型收敛,具体方法见下文;(3)随着加载的进行,局部出现畸变单元引起计算终止,通常需要网格重划分获得更好的网格质量、调整网格类型或采用其他大变形计算方法(ALE、CEL、SPH等)进行控制。
阻尼的添加方式主要由:(1)单元引入阻尼;(2)分析歩引入阻尼。
1、inp文件添加载荷步阻尼:
-
*Static, stabilize=0.0002, allsdtol=0.05, continue=NO
-
*Static, stabilize, factor=0.0002, allsdtol=0, continue=NO
-
*Static, stabilize, allsdtol=0.05, continue=YES
2、inp文件添加单元阻尼:
- *Solid Section, elset=Set-1, controls=EC-1, material=Material-1*Section Controls, name=EC-1, VISCOSITY=0.011., 1., 1.
机理分析
在涉及不收敛问题时,有的时候要了解非线性有限元(ABAQUS)的求解过程,为深入了解不收敛的本质提供基础:
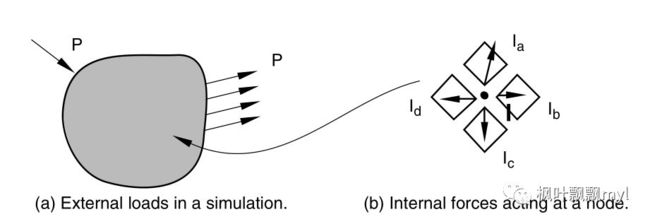
1、有限元何时算收敛:For the body to be in equilibrium, the net force acting at every node must be zero. Therefore, the basic statement of equilibrium is that the internal forces, I, and the external forces, P, must balance each other:
P-I=0
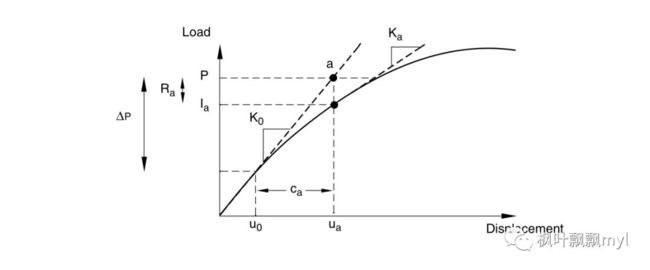
In a nonlinear problem Ra will never be exactly zero, so Abaqus/Standard compares it to a tolerance value, If Ra=P-Ia is less than this force residual tolerance at all nodes, Abaqus/Standard accepts the solution as being in equilibrium. By default, this tolerance value is set to 0.5% of an average force in the structure, averaged over time.
However, before Abaqus/Standard accepts the solution, it also checks that the last displacement correction, is small relative to the total incremental displacement, If is greater than a fraction (1% by default) of the incremental displacement, Abaqus/Standard performs another iteration. Both convergence checks must be satisfied before a solution is said to have converged for that time increment.
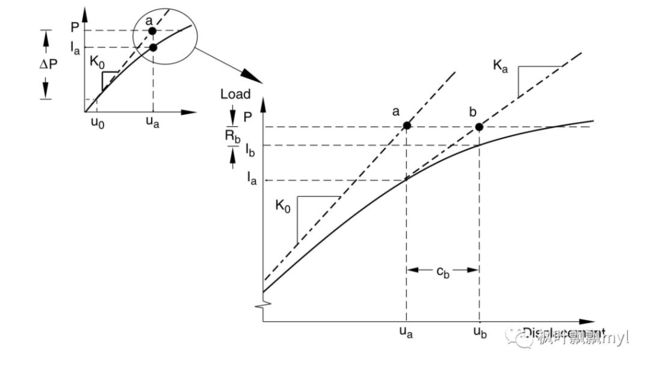
If the solution from an iteration is not converged, Abaqus/Standard performs another iteration to try to bring the internal and external forces into balance. First, Abaqus/Standard forms the new stiffness, Kafor the structure based on the updated configuration, ua, This stiffness, together with the residual, Ra determines another displacement correction, cb, that brings the system closer to equilibrium.
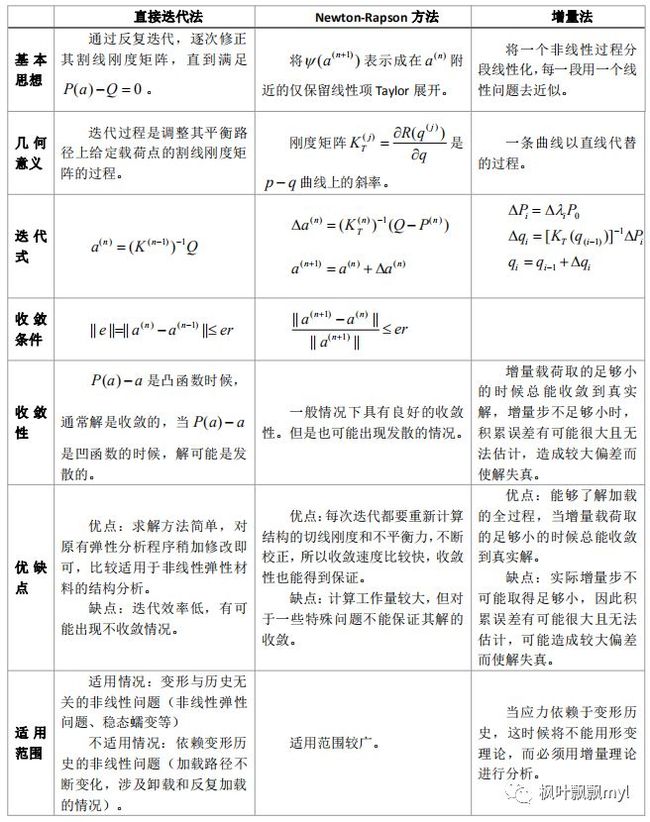
附:非线性方程的求解方法