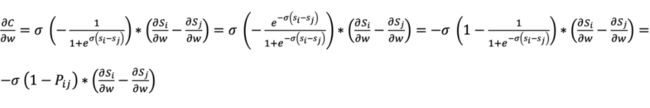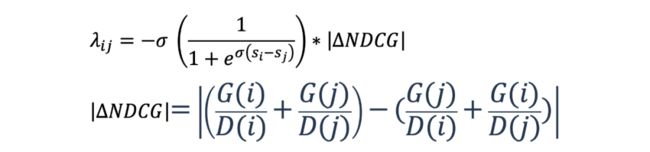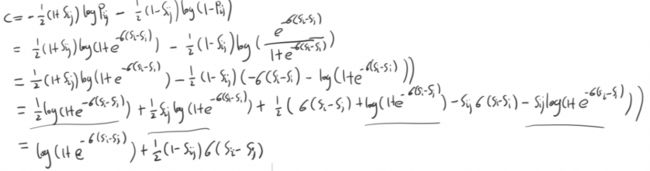排序学习（LTR）经典算法：RankNet、LambdaRank和LambdaMart

©PaperWeekly 原创 · 作者 | yancy

单位 | 字节跳动

研究方向 | 推荐系统

背景

在许多场景中我们都需要模型学习到排序的能力，比如网页搜索场景下我们需要根据搜索词和文档的相关度做排序，把更相关的文章排到前面，此时文章的相关度就是要排序的目标。又比如在视频推荐场景下，粗排的目标往往是学习精排，把精排认为更好的文章送入精排打分，此时视频的精排打分就是要排序的目标。Learn to Rank（LTR）要做的就是输入一批候选（上文中的网页或者视频），算法能够给出一种排序，使得这种排序最优秀。本文介绍 LTR 中经典的三种算法：RankNet、LambdaRank、LambdaMart，并介绍他们的关联。

评价指标

我们如何评价模型给出的顺序好还是坏呢？业界最常用的指标为 NDCG，大名鼎鼎的 Softrank、LambdaMart 都是以 NDCG 为准描述论文，在实践中 NDCG 也是最为常用的指标，下面对其进行介绍。

首先我们那需要先计算 DCG，我们有 T 个需要排序的候选，其中 表示算法给出的第 i 个位置的 label，比如搜索场景中文章相关性分为五个档次：非常相关、相关、中性、不相关、非常不相关，那对应的 label 分别就是 5，4，3，2，1。对应推荐粗排场景，可以直接使用精排的打分作为 label。分母则对位置做折算，越靠前的位置越重要。这个也比较符合直觉，我们搜索之后得到结果也是会更关注靠前的网页是否能快速满足我们的兴趣，如果前面几个结果相关性较差，我们更容易认为算法的表现不尽人意。如果没有这个分母的位置折算的话，不管算法如何排序，得到的反馈都是一样的。可以看出如果算法把分数更高的候选排的越靠前，DCG 也就越高。

DCG 计算出来的分数是一个考虑位置折算的累积收益，绝对值大小 的量纲有直接的关系，我们很难通过 DCG 的绝对值来判断算法的效果，不具备直观性，因此引出 NDCG：我们按照 label 倒排，得到最优的排序，计算这个排序下的 DCG，这就是我们算法能达到的最优上限 maxDCG，用 DCG/maxDCG 就得到了最终的 NDCG 指标，所以 NDCG 是一个介于 0-1 之间的值，值越大算法效果越好。

RankNet

从上面的计算公式可以看出 NDCG 是不可直接求导的，因为其中涉及到排序这种算子，这个本身就是不连续不可求导的，也就是论文中经常提到的 LTR 任务是 Non-Smooth 的原因。RankNet 解决排序的思路其实是把一个 list 排序的问题转化成 list 中两两比较的问题，举个例子来说比如你想买房子，给你一堆房源你很可能挑花眼，很难给出正确的排序。但是只给你两个做比较，你就可以从价格、面积、朝向这些维度进行比较，比较容易得出孰优孰略的结论，如果你具备了两两比较的能力，那用这个能力给出整体的排序就水到渠成了。

所以 RankNet 的训练数据不是输入一个一个的 list，而是输入一个一个的 pair，比如文章（i , j）。我们也知道 i 和 j 的 label。

模型对两个候选给出的打分为 。我们建模的目标是一个概率，即模型认为候选 i 比候选 j 更相关的概率：

这里注意 只是一个超参常数，并不是 sigmoid 函数，论文中使用了这种 notation，本文也进行了保留。其实实践中基本都是设置为 1。既然是要最大化概率，那用我们在二分类领域最熟悉的交叉熵损失：

其中 的意义为如果 i 的 label 比 j 大（i 比 j 更相关）则为 1，认为是正例。如果 i 的 label 比 j 小为 -1，认为是负例。如果打平则为 0。这里的 或者 就是模型输出的 logit，可以是神经网络不过 sigmoid 输出的最后一层 logit，也可以是简单的 LR 的输出，没有任何模型上的限制。RankNet 只是在 loss 层做了修改，可以适配 pointwise 中的所有模型结构。模型通过上述方式训练完成后，只需要在预测的时候得到每个文档的 logit ，按照这个得分倒排即可。

这里既然提到了 pointwise，可以稍微拓展讲一下 pointwise 算法。继续拿上文提到的网页搜索举例子，pointwise 的思路就是不需要标注一次搜索后网页的相关性，而是根据用户的行为决定正负例。如果一个网页曝光后点击就是正例，否则为负例。一般模型特征会加入 query 类和网页类以及 context 特征。

最后模型输出的是一个网页会不会被点击的概率，评价指标往往是 auc、F1 这种不考虑 list 顺序的指标。按照这个概率倒排作为排序的标准。从这里可以看出 pointwise 模型并不会考虑一次搜索结果后各网页之间的关系，并不是从全局的排序关系来考虑问题的，因此得到的排序结果也可能不是最优的。而 pair-wise 和 list-wise 算法则会建模 list 各元素的相关关系。

RankNet的加速

看到这里很多读者已经发现了 rankNet 的复杂度极其高，比如需要排序的 list 有 3 个候选的时候，我们就需要两两拆分成 6 个 pair 来训练。但其实我们可以做优化，首先我们可以利用 pair loss 的对称性减少一半的计算量。观察我们的 loss：

这里就是简单的推导和合并同类项，详细的过程参考附录。对于一个 pair(i,j)，我们假设 i 的相关性比 j 更强，也就是 ，这时候产生的 loss：。

如果我们把这个 pair 反过来，也就是（j,i），这时 。产生的 loss：

所以 pair 调换顺序产生的 loss 是完全一样的，因此我们只需要考虑 i 比 j 更相关的 pair 即可，接下来我们对模型参数求导：

首先基于公式（1）求导：

观察上述两个公式，易得：

假设模型内部用到的参数为 w，则利用链式法则和公式（2）（3）得到：

我们把

402 Payment Required

这一项定义为 ，则有

再结合上面提到的 pair loss 对称性，我们定义一个 pair 集合：I:{i,j}，其中 ，我们只需要计算 I 集合的 loss，则：

其中 这里 的数学表达比较绕，其实说白了就是针对一个文档 i，找出所有 label 比 i 小的文章 j，然后把这些 全部加起来。然后找到所有 label 比 i 大的文章 j，然后把这些 也全部加起来，两部分和一减变得到了 。你可能觉得这个推导非常难，其实举个只有三个文档的例子你就懂了：

加入三篇文章 1，2，3 的 label 依次减少。记得我们前面提到的 pair loss 对称性，我们只需要关注 i 比 j  label 更高的 pair 即可。则 I = {(1,2),(1,3),(2,3)}，带入公式（5）有：

这里文章 1 得分最高，所以碰到谁都可以欺负，因此 都是正的。文章 2 能欺负文章 3，但是欺负不了 1，因此 符号是正的， 符号是负的。文章 3 最弱，碰到谁都是负号。

写到这里可能有同学会问，我们大费周折得到这样的合并有什么好处的，我来告诉你好处大大的，因为合并之后每个 都只要计算一次，如果不合并的话 是不是要 bp 两次，但是现在只需要 bp 一次，和 point-wise 的复杂度是一模一样的。多出来的计算量只是在 fp 的时候计算 。

LambdaRank

基于公式（4）并利用 pair loss 对称性，我们对 w 的梯度做一定的变形：

这里可以看出来 和 肯定是异号的，当优化器想让 C 减少的时候， 肯定是增加的，同时 是同等程度的减少，并且增加或者减少的幅度和 相关，如果 越小， 增加的更多。 越小表示模型认为候选 i 比 j 差的概率更高，注意我们约定 pair 是 i 肯定是比 j 更相关的，那说明模型错误的更多，这个时候把 i 和 j 分的更开是很符合我们的直觉的。

这里我们看出 表明了模型把 ij 分开的动力有多大，因为 rankNet 仅考虑 pair 的顺序，并不考虑 i 或者 j 处在的位置，比如针对 NDCG 指标，校准第一二位置的乱序以及倒数一二位置的乱序得到的 NDCG gain 是完全不同的，但是 RankNet 无法感知到这两个 pair 重要性的不同。所以 LambdaRank 对 加入了一个启发式的权重：

表示交换 ij 位置之后对于 NDCG 的影响，表示的是当把 j 换到 i 之后 NDCG 能增加多少。 即 DCG 的分子部分：。 即 DCG 的分母部分：。如果 越大表示这个 pair 校准后对 NDCG 的影响越大，因此增加梯度，更加拉开 ij 的差距。Paper 也证明了这样的权重是可以直接优化 NDCG 的。如果你用的是其他指标，也直接把对应指标的变化放在这里就可以直接对指标进行优化。

最后再提一句：LambdaMart 其实就是 lambdaRank 的 gbdt 树版本。至此 RankNet 和 LambdaRank 已经介绍完毕，可以看出这里还是用 pairwise 的思路来解决 listwise 的问题。欢迎对这两个算法感兴趣的同学在文章下面留言，大家一起进行讨论。后续我会继续分享 softRank，直接使用概率论的思路把排序变成一个可求导的问题，思路非常巧妙。如果大家对一些算法特别感兴趣也可以留言，我抽时间进行研读后来和大家进行讨论。如果本文对您有帮助，希望能不吝点赞、评论和分享，这是对我的最大帮助！

附录

损失函数的推导：

参考文献

[1]Burges, Christopher JC. "From ranknet to lambdarank to lambdamart: An overview." Learning 11, no. 23-581 (2010): 81.

[2]C.J.C. Burges, R. Ragno and Q.V. Le. Learning to Rank with Non-Smooth Cost Functions. Advances in Neural Information Processing Systems, 2006.

特别鸣谢

感谢 TCCI 天桥脑科学研究院对于 PaperWeekly 的支持。TCCI 关注大脑探知、大脑功能和大脑健康。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

 投稿通道：

• 投稿邮箱：[email protected] 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·