【深度学习】生成模型:VAE(自编码器)模型解析
目录
- 1 前言
- 2 VAE模型
-
- 2.1 VAE模型推导
- 2.2 重参化技巧
- 3 QA
-
- 3.1 生成体现在什么地方
- 3.2 AE和VAE的区别
- 4 另一种角度理解VAE
- 5 总结
- 不足
- 6 参考文献
1 前言
本文为自己自学内容的记录,其中多有借鉴别人博客的地方,一并在参考文献中给出链接,其中大部分截图来自李宏毅深度学习PPT课件。其中内容有理解不到位的地方,各位大佬在评论区给出修改意见,感恩。
本文前置知识高斯混合模型和EM算法,如果不了解这两种算法直接看VAE模型会有理解上的障碍。
2 VAE模型
2.1 VAE模型推导
VAE模型的初始化推导和EM算法的推导有相似之处,不同的是在VAE模型中隐变量 Z Z Z是一个连续的无穷维而不是跟高斯分布一样为有限的离散变量,所以在VAE的参数估计中用到了神经网络。
VAE是一个深度生成模型,其最终目的是生成出概率分布 P ( x ) P(x) P(x), x x x即输入数据。在VAE中,通过高斯混合模型(Gaussian Mixture Model)来生成 P ( x ) P(x) P(x),也就是说 P ( x ) P(x) P(x)是由一系列高斯分布叠加而成的,每一个高斯分布都有它自己的参数 μ \mu μ 和 σ \sigma σ。

为此假设隐变量 z z z服从 z ∼ N ( 0 , I ) \mathrm{z} \sim \mathrm{N}(0, \mathrm{I}) z∼N(0,I)(注意 z z z是一个向量,生成自一个高斯分布),并且找一个映射关系将向量 z z z映射成这一系列高斯分布的参数向量 μ ( z ) \mu(z) μ(z)和 σ ( z ) \sigma (z) σ(z)。有了这一系列高斯分布的参数,就可以得到叠加后的 P ( x ) P(x) P(x)的形式,即 x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) \mathrm{x} \mid \mathrm{z} \sim \mathrm{N}(\mu(\mathrm{z}), \sigma(\mathrm{z})) x∣z∼N(μ(z),σ(z))(这里的“形式”仅是对某一个向量 z z z所得到的)这里可以结合高斯混合模型理解,也可以结合参考文献【2】中的例子理解,总之就是假设隐变量 Z Z Z服从某一种分布,而观察到的样本 X X X属于 Z Z Z的某一个分布的概率。
那么要找的这个映射关系 P ( x ∣ z ) P(x|z) P(x∣z)如何获得?这里就需要用到神经网络,那么为什么不用极大似然估计,因为在VAE模型中隐变量数量假设是高维无限的,没有办法用积分去做,所以用神经网络去拟合(神经网络可以拟合任意函数)。如下图所示:
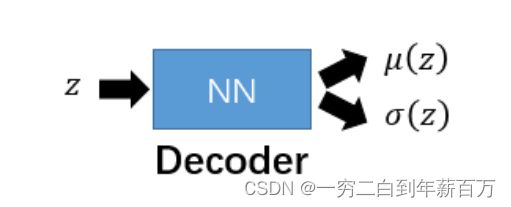
输入向量 z z z,得到参数向量 μ ( z ) \mu (z) μ(z)和 σ ( z ) \sigma (z) σ(z)。这个映射关系是要在训练过程中更新NN权重得到的。这部分作用相当于最终的解码器(decoder)。
对于某一个向量 z z z我们知道了如何找到 P ( x ) P(x) P(x),那么对连续变量 z z z依据全概率公式有:
P ( x ) = ∫ z P ( z ) P ( x ∣ z ) d z \mathrm{P}(\mathrm{x})=\int_{\mathrm{z}} \mathrm{P}(\mathrm{z}) \mathrm{P}(\mathrm{x} \mid \mathrm{z}) \mathrm{dz} P(x)=∫zP(z)P(x∣z)dz
但是很难直接计算积分部分,因为我们很难穷举出所有的向量 z z z用于计算积分。又因为 P ( x ) P(x) P(x) 难以计算,那么真实的后验概率 P ( z ∣ x ) = P ( z ) P ( x ∣ z ) / P ( x ) P(z∣x)=P(z)P(x∣z)/P(x) P(z∣x)=P(z)P(x∣z)/P(x) 同样是不容易计算的,这也就是为什么下文要引入 q ( z ∣ x ) q(z|x) q(z∣x)来近似真实后验概率 P ( z ∣ x ) P(z|x) P(z∣x)。
因此我们用极大似然估计来估计 P ( x ) P(x) P(x),有似然函数 L L L:
L = ∑ x log P ( x ) \mathrm{L}=\sum_{\mathrm{x}} \log \mathrm{P}(\mathrm{x}) L=x∑logP(x)
这里额外引入一个分布 q ( z ∣ x ) q(z|x) q(z∣x), z ∣ x ∼ N ( μ ′ ( x ) , σ ′ ( x ) ) z|x \sim N\big(\mu^\prime(x), \sigma^\prime(x)\big) z∣x∼N(μ′(x),σ′(x)),这个分布表示形式如下:

这个分布同样是用一个神经网络来完成,向量 z z z根据NN输出的参数向量 μ ′ ( x ) \mu '(x) μ′(x) 和 σ ′ ( x ) \sigma '(x) σ′(x) 运算得到,这部分作用相当于编码器(encoder)。
注意:这里为什么需要引入额外的分布 q ( z ∣ x ) q(z|x) q(z∣x),跟EM算法的求解过程做对比,在EM算法中 q ( z ) q(z) q(z)是可以取到 P ( z ∣ x ) P(z|x) P(z∣x),从而令散度等于零不断的抬升下界进行极大似然估计,但是在VAE中由于 P ( z ∣ x ) P(z|x) P(z∣x)是很难求的所以引入一个变量q(x)对其进行近似。
接下来进行公式的推导,由于在EM算法中已经推导出了ELBO+KL的形式,这里就直接拿来用:
log P ( x ∣ θ ) = ∫ Z q ( z ∣ x ) log P ( x , z ∣ θ ) q ( z ∣ x ) d z + D K L ( q ( z ∣ x ) ∥ P ( z ∣ x , θ ) ) \log P(\mathrm{x} \mid \theta)=\int_{Z} q(\mathrm{z}|\mathrm{x}) \log \frac{P(\mathrm{x}, \mathrm{z} \mid \theta)}{q(\mathrm{z}|\mathrm{x})} d \mathrm{z}+D_{K L}(q(\mathrm{z}|\mathrm{x}) \| P(\mathrm{z} \mid \mathrm{x}, \theta)) logP(x∣θ)=∫Zq(z∣x)logq(z∣x)P(x,z∣θ)dz+DKL(q(z∣x)∥P(z∣x,θ))
根据KL divergence的性质 D K L ( q ( z ∣ x ) ∥ P ( z ∣ x , θ ) ) ≥ 0 D_{K L}(q(\mathrm{z}|\mathrm{x}) \| P(\mathrm{z} \mid \mathrm{x}, \theta)) \geq 0 DKL(q(z∣x)∥P(z∣x,θ))≥0 当且仅当 q ( z ∣ x ) = P ( z ∣ x , θ ) q(\mathrm{z}|\mathrm{x})=P(\mathrm{z} \mid \mathrm{x}, \theta) q(z∣x)=P(z∣x,θ)取等号,因此有
log P ( x ∣ θ ) ≥ ∫ z q ( z ∣ x ) log P ( x , z ∣ θ ) q ( z ∣ x ) d z \log P(\mathrm{x} \mid \theta) \geq \int_{z} q(\mathrm{z}|\mathrm{x}) \log \frac{P(\mathrm{x}, \mathrm{z} \mid \theta)}{q(\mathrm{z}|\mathrm{x})} d \mathrm{z} logP(x∣θ)≥∫zq(z∣x)logq(z∣x)P(x,z∣θ)dz
因此便得到了 log P ( X ∣ θ ) \log P(X \mid \theta) logP(X∣θ)的一个下界称为Evidence Lower Bound (ELBO),简称 L b L_b Lb。最大化 L b L_b Lb 就等价于最大化似然函数 L L L。那么接下来具体看 L b L_b Lb :
L b = ∫ z q ( z ∣ x ) log P ( z , x ) q ( z ∣ x ) d z = ∫ z q ( z ∣ x ) log ( P ( z ) q ( z ∣ x ) ⋅ P ( x ∣ z ) ) d z = ∫ z q ( z ∣ x ) log P ( z ) q ( z ∣ x ) d z + ∫ z q ( z ∣ x ) log P ( x ∣ z ) d z = − D K L ( q ( z ∣ x ) ∥ P ( z ) ) + ∫ z q ( z ∣ x ) log P ( x ∣ z ) d z = − D K L ( q ( z ∣ x ) ∥ P ( z ) ) + E q ( z ∣ x ) [ log P ( x ∣ z ) ] \begin{aligned} \mathrm{L}_{\mathrm{b}} &=\int_{z} \mathrm{q}(\mathrm{z} \mid \mathrm{x}) \log \frac{\mathrm{P}(\mathrm{z}, \mathrm{x})}{\mathrm{q}(\mathrm{z} \mid \mathrm{x})} \mathrm{dz} \\ &=\int_{\mathrm{z}} \mathrm{q}(\mathrm{z} \mid \mathrm{x}) \log \left(\frac{\mathrm{P}(\mathrm{z})}{\mathrm{q}(\mathrm{z} \mid \mathrm{x})} \cdot \mathrm{P}(\mathrm{x} \mid \mathrm{z})\right) \mathrm{dz} \\ &=\int_{\mathrm{z}} \mathrm{q}(\mathrm{z} \mid \mathrm{x}) \log \frac{\mathrm{P}(\mathrm{z})}{\mathrm{q}(\mathrm{z} \mid \mathrm{x})} \mathrm{dz}+\int_{\mathrm{z}} \mathrm{q}(\mathrm{z} \mid \mathrm{x}) \log \mathrm{P}(\mathrm{x} \mid \mathrm{z}) \mathrm{dz} \\ &=-\mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z}))+\int_{\mathrm{z}} \mathrm{q}(\mathrm{z} \mid \mathrm{x}) \log \mathrm{P}(\mathrm{x} \mid \mathrm{z}) \mathrm{dz} \\ &=-\mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z}))+\mathrm{E}_{\mathrm{q}(\mathrm{z} \mid \mathrm{x})}[\log \mathrm{P}(\mathrm{x} \mid \mathrm{z})] \end{aligned} Lb=∫zq(z∣x)logq(z∣x)P(z,x)dz=∫zq(z∣x)log(q(z∣x)P(z)⋅P(x∣z))dz=∫zq(z∣x)logq(z∣x)P(z)dz+∫zq(z∣x)logP(x∣z)dz=−DKL(q(z∣x)∥P(z))+∫zq(z∣x)logP(x∣z)dz=−DKL(q(z∣x)∥P(z))+Eq(z∣x)[logP(x∣z)]
推导到这一步就会发现这种形式的公式是看VAE相关论文经常给出的形式。同时到了这一步也可以看出,最大化似然函数 L L L就是最大化 L b L_b Lb,也即最小化 − D K L ( q ( z ∣ x ) ∥ P ( z ) ) -\mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z})) −DKL(q(z∣x)∥P(z))和最大化 E q ( z ∣ x ) [ log P ( x ∣ z ) ] \mathrm{E}_{\mathrm{q}(\mathrm{z} \mid \mathrm{x})}[\log \mathrm{P}(\mathrm{x} \mid \mathrm{z})] Eq(z∣x)[logP(x∣z)]。
- 最小化 − D K L ( q ( z ∣ x ) ∥ P ( z ) ) -\mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z})) −DKL(q(z∣x)∥P(z)),使后验分布近似值 q ( z ∣ x ) q(z|x) q(z∣x)接近先验分布 P ( z ) P(z) P(z)。也就是说通过 q ( z ∣ x ) q(z|x) q(z∣x)生成的编码 z z z不能太离谱,要与某个分布相当才行,这里是对中间编码生成起了限制作用。当 q ( z ∣ x ) q(z|x) q(z∣x)和 P ( z ) P(z) P(z)都是高斯分布时,推导式有(参考文献【4】中Appendix B):
D K L ( q ( z ∣ x ) ∥ P ( z ) ) = − 1 2 ∑ j J ( 1 + log ( σ j ) 2 − ( μ j ) 2 − ( σ j ) 2 ) \mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z}))=-\frac{1}{2} \sum_{\mathrm{j}}^{\mathrm{J}}\left(1+\log \left(\sigma_{\mathrm{j}}\right)^{2}-\left(\mu_{\mathrm{j}}\right)^{2}-\left(\sigma_{\mathrm{j}}\right)^{2}\right) DKL(q(z∣x)∥P(z))=−21j∑J(1+log(σj)2−(μj)2−(σj)2)
其中 J J J表示向量 z z z的总维度数, σ j \sigma_j σj和 μ j \mu_j μj表示 q ( z ∣ x ) q(z|x) q(z∣x)输出的参数向量 σ \sigma σ和 μ \mu μ的第 j j j个元素。(这里的 σ \sigma σ和 μ \mu μ等于前文中 μ ′ ( x ) \mu '(x) μ′(x)和 σ ′ ( x ) \sigma '(x) σ′(x). - 最大化 E q ( z ∣ x ) [ log P ( x ∣ z ) ] \mathrm{E}_{\mathrm{q}(\mathrm{z} \mid \mathrm{x})}[\log \mathrm{P}(\mathrm{x} \mid \mathrm{z})] Eq(z∣x)[logP(x∣z)],即在给定编码器输出 q ( z ∣ x ) q(z|x) q(z∣x)下解码器输出 P ( x ∣ z ) P(x|z) P(x∣z)越大越好。这部分也就相当于最小化Reconstruction Error(重建损失)
由此我们可以得出VAE的原理图:
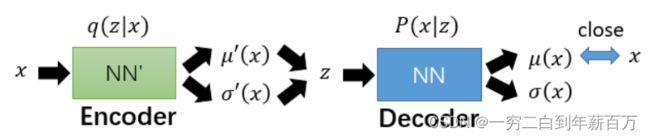
通常忽略掉decoder输出的 σ ( x ) \sigma(x) σ(x)一项,仅要求 μ ( x ) \mu(x) μ(x)与 x x x越接近越好。
对某一输入数据 x x x来说,VAE的损失函数即( L b L_b Lb取负号):
min Loss V A E = D K L ( q ( z ∣ x ) ∥ P ( z ) ) − E q ( z ∣ x ) [ log P ( x ∣ z ) ] \min \operatorname{Loss}_{\mathrm{V} \mathrm{AE}}=\mathrm{D}_{\mathrm{KL}}(\mathrm{q}(\mathrm{z} \mid \mathrm{x}) \| \mathrm{P}(\mathrm{z}))-\mathrm{E}_{\mathrm{q}(\mathrm{z} \mid \mathrm{x})}[\log \mathrm{P}(\mathrm{x} \mid \mathrm{z})] minLossVAE=DKL(q(z∣x)∥P(z))−Eq(z∣x)[logP(x∣z)]
2.2 重参化技巧
在前面VAE的介绍中样本经过Encoder生成了隐变量的一个分布 z ∼ q ( z ∣ x ) \mathrm{z} \sim \mathrm{q}(\mathrm{z} \mid \mathrm{x}) z∼q(z∣x),然后从这个分布中采样 z z z进行Decoder,注意“采样”这个操作是不可微的,因此不能做反向传播,所以用reparameterization trick来解决这个问题,示意图如下:

将上图左图原来的采样操作通过reparameterization trick变换为右图的形式。
我们引入一个外部向量 ϵ ∼ N ( 0 , I ) ϵ∼N(0,I) ϵ∼N(0,I),通过 z = μ + σ ⊙ ϵ z = μ + σ ⊙ ϵ z=μ+σ⊙ϵ计算编码 z z z ( ⊙ \odot ⊙表示element-wise乘法, ϵ \epsilon ϵ的每一维都服从标准高斯分布即 ϵ i ∼ \epsilon_i \sim ϵi∼ N(0,1),由此loss的梯度可以通过 μ \mu μ和 σ \sigma σ分支传递到encoder model处( ϵ \epsilon ϵ并不需要梯度信息来更新)。
这里利用了这样一个事实[3]:考虑单变量高斯分布,假设 z ∼ p ( z ∣ x ) = N ( μ , σ 2 ) z∼p(z∣x)=N(μ,σ 2 ) z∼p(z∣x)=N(μ,σ2),从中采样一个 z z z,就相当于先从 N ( 0 , 1 ) N(0,1) N(0,1)中采样一个 ϵ \epsilon ϵ,再令 z = μ + σ ⊙ ϵ z=\mu + \sigma \odot \epsilon z=μ+σ⊙ϵ
3 QA
3.1 生成体现在什么地方
3.2 AE和VAE的区别
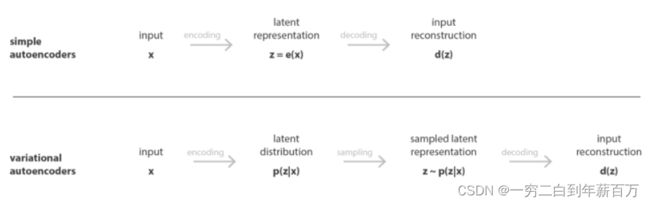
将把 x x x表示为输入数据,把 z z z表示为潜在变量(编码表示)。在普通的自编码器中,编码器将输入 x x x转换为潜在变量 z z z,而解码器将 z z z转换为重构的输出。而在可变自编码器中,编码器将 x x x转换为潜在变量 p ( z ∣ x ) p(z|x) p(z∣x)的概率分布,然后对潜在变量 z z z随机采样,再由解码器解码成重构输出。自编码器(确定性)和可变自编码器(概率性)的区别。
4 另一种角度理解VAE
5 总结
其实那么多数学公式推导,我自己都有点晕,但是本质上就是用自编码器去产生很多高斯分布,去拟合样本的分布,然后某个x对应的高斯分布里采样z,然后复原成x,跟GAN区别就是这个是完全去模仿分布,只能生成数据中已有的图片,很难创造新的图片,最多也就是插值图片了。
也可以理解成图片的特征向量z采样于某种高斯分布,我们要把他给找出来,我们希望这个分布贴近标准正太分布,然后通过编码器生成对应均值和方差,然后采样z,希望z又能复原图片,这样就找到了这个z背后的高斯分布。这个高斯分布的均值就是最大概率生成特征z,可以复原图片,当然均值旁边采样出来的z可能可以复原的不是很像,但是也是在数据集里的,如果有2个图片的特征分布都在这个点有所重合的话,可能就是2个图片中间的插值图片了。
不足
VAE在产生新数据的时候是基于已有数据来做的,或者说是对已有数据进行某种组合而得到新数据的,它并不能生成或创造出新数据。另一方面是VAE产生的图像比较模糊。
而大名鼎鼎的GAN利用对抗学习的方式,既能生成新数据,也能产生较清晰的图像。后续的更是出现了很多种变形。
6 参考文献
[1]【深度学习】VAE(Variational Auto-Encoder)原理
[2]【干货】深入理解变分自编码器
[3]变分自编码器VAE:原来是这么一回事 | 附开源代码
[4]Auto-encoding variational bayes
[5]【机器学习】白板推导系列(三十二) ~ 变分自编码器(VAE)
[6]PyTorch实现VAE
[7]使用(VAE)生成建模,理解可变自动编码器背后的数学原理