读书笔记《Outlier Analysis》 第五章 高维数据中的异常检测:子空间方法
1.基本介绍
现实世界中,很多数据的维度非常高,许多传统的异常检测方法在高维数据中无法有效工作。这也叫维度灾难/维度诅咒/维度惩罚。
在高维空间中,当进行全维分析时,数据变得稀疏,真正的异常值被多个不相关维数的噪声效应所掩盖。
维度灾难的一个主要原因是在高维情况下,难以定义一个点的相关局部性。例如,在高维空间中,所有点对几乎是等距的。这种现象被称为数据稀疏或距离集中。而异常值是定义为稀疏区域中的数据点,这导致了一种鉴别性差的情况,即所有数据点都位于几乎相同的稀疏区域中,具有全维度。
1.1 局部相关维度
局部相关维度:一个物体可能有几个被测量的量,这个物体的显著异常行为可能只反映在这些量的一小部分中。
也即,一小部分的测量的数据中可能可以找到异常值,因为数据维度不高,但是当来自测量的数据以全维度表示时,异常数据点将在几乎所有数据视图中显式为正常。即大量正常测量的噪声变化将掩盖异常值。
因此,异常值通常嵌入到局部相关的子空间中。
因此,探索低维子空间以获得感兴趣的偏差是有意义的。这种方法过滤掉了大量维数的加性效应,并导致了更健壮的异常值。
1.2 投影异常值检测 / 子空间异常值检测
在缺少属性值的数据集中,这种低维投影也经常可以被识别。这对于许多实际问题是有用的。因为很多情况下,特征提取是一个困难的过程,并且通常存在不完整的特征描述。
例如,在机身故障检测中,可能只应用了一个测试子集,因此只有一个维度子集的值可以用于异常分析。
这种模型称为投影异常值检测,或叫做子空间异常检测。
1.3 相关子空间的识别
相关子空间的识别是一个非常具有挑战性的问题。 这是因为高维数据的可能投影数与数据的维数呈指数关系。 一种有效的离群点检测方法需要对数据点和维数进行综合搜索,以揭示最相关的离群点。 这是因为不同的维度子集可能与不同的异常值相关。
一般来说,为每个数据点选择一个单一的相关子空间会导致不可预测的结果,因此,将来自多个子空间的结果组合起来是很重要的。换句话说,子空间的异常检测本质上是一个以集合为中心的问题。
1.4 识别子空间的几类常用方法
基于稀有性:
这些方法视图从底层分布的稀有性来发现子空间。这里的主要挑战是计算,因为在高维中,稀有子空间的数量远远大于密集子空间的数量。
无偏:
在这些方法中,子空间是以无偏的方式采样的,并且分数被组合在采样的子空间上。
当子空间从原始属性集采样时,该方法称为特征袋。
在任意定向的子空间被采用的情况下,该方法被称为旋转袋或旋转子空间采样。
虽然这些方法很简单,但是通常工作的很好。
基于聚合的方法:
在这些方法中,聚合统计 (如数据的全局或局部子集的聚类统计、方差统计或非均匀统计) 用于量化子空间的相关性。
与基于稀有的统计不同,这些方法量化了全局或局部参考集的统计属性,而不是试图直接识别很少填充的子空间。
由于这类方法仅提供弱提示(且易于出错)来标识相关子空间,因此采样多个子空间是至关重要的。
2.Axis-Parallel Subspaces轴-并行子空间(组合多个子空间采样)
2.1 基本介绍
在轴-平行子空间方法中,异常值是由轴-平行子空间定义的。在这些方法中,是在原始数据的特征子集中定义一个异常值。然后需要仔细量化这样才能比较各个子空间的得分。除此之外,还需要量化各种子空间在暴露异常值方面的有效性的方法。
轴-平行方法使用的方法有两个主要变化:
第一类方法:逐个点地检测,并确定其相关的外围子空间。这本质上是一种基于实例的方法。显然,计算上是昂贵的。但是该方法提供了细粒度的分析,也助于提供内涵知识(即解释一个点为什么是异常点)。
第二类方法:通过预先建立子空间模型来识别异常值。通过模型对每个点进行评分。在某些情况下,每个模型可能对应于单个子空间。分数通常是通过使用不同模型获的结果的集成分数来评分的。组合分数往往会增强分数的局部子空间特性,因为集成方法(集成学习)能够减少表示偏差。
这类方法如特征袋、旋转袋、子空间直方图和隔离森林。
在子空间分析中,基于集成的分析是很重要的。由于来自不同子空间的异常值分数可能有很大的不同,因此通常很难完全信任来自单个子空间的分数,组合多个子空间的结果分数是很重要的。
本章主要探讨的是利用组合多个子空间的优点的几种方法。
2.2 异常检测的遗传算法
子空间异常值是通过在低维空间中找到具有异常低密度的数据局部区域来识别的。
可以利用遗传算法来寻找这种局部子空间区域。然后,异常值由它们在这些区域的成员组成来定义。
2.2.1 定义异常低维投影
为了识别异常的低维投影,重要的是要提供适当的统计数据来定义异常的低维投影。
异常的低维投影是指数据密度特别低于平均值的投影。
可以使用基于网格的方法来识别稀疏填充的局部子空间区域。
2.2.2 定义子空间搜索的遗传算子
由于指数计算的复杂性,对所有子空间进行详尽的搜索是不切实际的。 因此,需要一种选择性搜索方法,它将大部分子空间修剪。 这个问题的本质是,在满足稀疏条件的基于网格的子空间上没有向上或向下封闭的属性。 在频繁的模式挖掘等其他问题中,这些属性经常被利用。 然而,与频繁的模式挖掘不同,在频繁的模式挖掘中,人们正在寻找频率较高的模式,寻找维度的稀疏子集的问题具有在干草堆中找到针头的味道。
(选择————交叉————变异)
2.3 寻找基于距离的外围子空间
书中一开始提到了HOS-Miner算法,这里有一篇论文《HOS-Miner: A System for Detecting Outlying Subspaces of High-dimensional Data》专门讲这个算法用于检测高维数据中的外围子空间,附上论文链接(https://eprints.usq.edu.au/5654/1/Zhang_Lou_Ling_Wang_VLDB%2704_AV.pdf)
数据X的外围子空间的定义:
For a given data point X , determine the set of subspaces such that the sum of its k -nearest neighbor distances in that subspace is at least δ .对于一个给定的数据点X,确定子空间的集合,使得它在该子空间中的K最近邻距离之和至少为δ。
随着维数的增加,子空间更有可能是外围的。
可以利用不同剪枝特性和遗传算法寻找外围子空间。
2.4 特征袋:一种子空间采样的视角
组合来自多个子空间的异常值的最简单的方法是使用特征袋,这是一种集成方法(集成学习:三个臭皮匠,赛过一个诸葛亮)。
集成的每个基本组件使用以下步骤:
第一步:随机从(d/2)到(d−1)中选择一个整数r。【注:(d/2)是向下取整】
第二步:从迭代t中的底层数据集随机选择r特征(不替换),以便在第t次迭代中创建r维数据集Dt。
第三步:将离群点检测算法Ot应用于数据集上,以便计算每个数据点的得分。
总结以下就是:在定义域内随机选择整数r,然后选择r个特征以创建数据集Dt,最后将异常检测算法运用在该数据集上,并计算每个数据点的得分。
原则上,在每次迭代中,可以使用不同的离群点检测算法,前提是在过程结束后将分数归一化为Z值(Z值计算:减去均值再除以标准差)。 规范化也是必要的,以解释不同的子空间样本包含不同数量的特征。 然而,有研究者也使用LOF算法(局部异常因子)进行所有迭代。
在过程结束时,组合来自不同算法的离群点分数有以下两种可能的方式之一:
广度优先方法:在这种方法中,算法的排序用于组合目的。 在所有不同的执行中,排名第一的异常值被排在第一位,其次是排名第二的异常值(删除重复),以此类推。 由于某一特定等级内的异常值之间的连接断裂,可能存在微小的变化。
累加和方法:汇总了不同算法执行的离群点分数。 排名靠前的离群点在此基础上被检测出来。 人们还可以将此过程视为等同于集成方法(集成学习)中的平均组合函数。
子空间采样可以对大量子空间进行采样,以提高鲁棒性。
使用集成方法可以降低表示的偏差。
2.5 投影聚类集合
Projected clustering methods defifine clusters as sets of points together with sets of dimensions in which these points cluster well.
1、【投影聚类方法将聚类定义为点的集合(一组点)和维度集合(一组维度),这些维度中的点可以很好地聚类。】
在第四章提到聚类和异常检测是互补关系。那是否也可以将投影或子空间聚类用于异常检测。
使用投影聚类算法的集合进行异常检测:
1.在数据集上使用像PROCLUS这样的随机投影聚类方法来创建一组投影集群。
2.根据每个点与它所属的簇的相似度,量化其离群值。 相关分数的示例包括大小、尺寸、到群集质心的(预计)距离或这些因素的组合。 正确的度量选择对所使用的特定聚类算法敏感。
了解这种基于聚类的方法的关键点是,虽然以集成为中心的方法对于成功至关重要,但是发现的异常值类型对底层聚类很敏感。 因此,局部敏感的聚类集成将使离群点局部敏感。 一个对子空间敏感的聚类集合将使离群值对子空间敏感,而对相关敏感的聚类集合将使离群值对相关性敏感。
2.6 线性时间的子空间直方图
具有散列的子空间直方图的线性时间,并称为RS-Hash。基本思想是在大小为s的数据样本上重复构建基于网格的直方图,并以集成为中心的方法组合分数。每个直方图都构建在数据的随机选择子空间上。子空间的维数和网格区域的大小特定于其集合分量的。在集成组件的测试阶段,根据网格区域中(来自训练样本的)点数的对数对数据中的所有N点进行评分。对多个大小为s的样本重复该方法。将针对特定点的分数在不同的集成组件上取平均值,以创建最终结果,该结果非常可靠。网格区域的尺寸和大小的变化由整数维数参数r和分数网格大小参数f∈(0,1)控制,它们在不同的集成分量中随机变化。
2.7 隔离森林
隔离森林也是用于聚类的极随机聚类森林(ERC-Fore st)的特例。
隔离森林是一组隔离树的集合组合。在隔离树种,使用轴-平行切割在随机选择的属性中的随机选择的分区点上对数据进行递归分区,以便将实例隔离到具有越来越少实例的节点中,直到将这些点隔离成包含一个实例的单例节点。在这种情况下,包含异常值的树枝的深度明显较小,因为这些数据点位于稀疏区域中。因此,将叶子到根的距离用作异常值。通过平均隔离森林的不同树中数据点的路径长度来执行最终组合步骤。
还有另一篇比较通俗易懂的博客基于孤立/隔离森林的异常检测。
2.8 选择高对比度的子空间(HiCS)
特征袋中讨论了随机样本子空间,如果许多维度是不相关的,那么至少有几个维度很可能包含在每个子空间样本中。同时,由于许多维度被丢弃,导致信息丢失。这些影响不利于方法的准确性。因此,是否有可能执行一个预处理,其中选择少数量的高对比度子空间。这种方法也被称为HiCS,因为它是选择高对比度的子空间。
高对比度子空间:当在子空间里可以明确的分辨出离群点和其他数据对象时,将赋予该子空间很高的对比度值。
2.9 子空间投影的局部选择
可以使用相关子空间投影的局部统计选择来识别异常值。换句话说,子空间投影的选择针对特定数据点进行了优化,因此给定数据点的位置在选择过程中至关重要。
2.10 基于距离的参考集
有一种基于距离的方法,用于在数据的低维投影钟寻找离群点。在这种方法中,不是试图在整个数据中找到异常低密度的局部子空间,而是针对每个数据点提供局部分析。对于每个数据点X,识别一个点S(X)的参考集。参考集S(X)被生成为最接近候选点的顶部k点,使用共享最近邻距离。
3 .广义子空间(即任意定向的子空间)
3.1 基本介绍
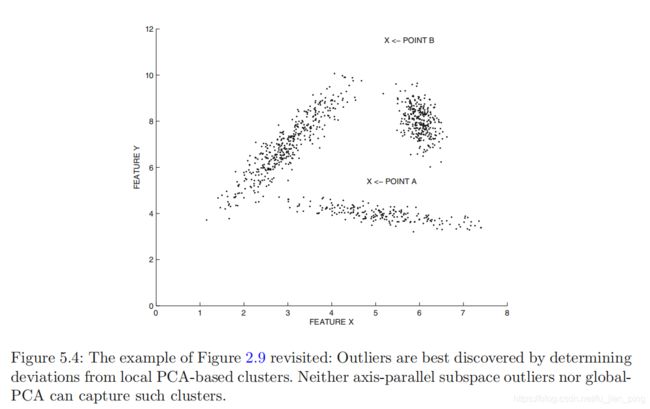
尽管轴平行方法对于在大多数实际设置中查找离群值有效,但在点沿数据的任意低维流形对齐的情况下,对查找离群值不是很有用。 例如,在下图图5.4的情况下,二维数据中没有一维特征可以找到离群值。 另一方面,可以找到局部的一维相关子空间,以便大多数数据沿着这些局部的一维子空间对齐,并且剩余的偏差可以分类为离群值。 尽管此特定数据集由于其维数较低而似乎相对容易检测到异常值,但是随着维数的增加,此问题可能会变得更具挑战性。
广义子空间算法是由以下两个思想来推广的:
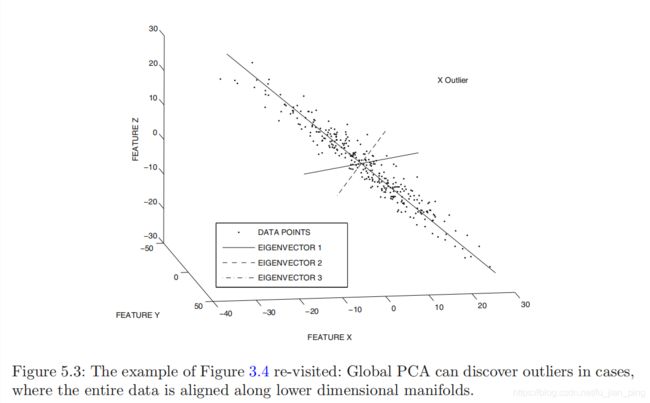
基于PCA的线性模型可以发现数据中的全局相关区域。例如,在上图5.3的情况下,可以通过确定这些全局相关方向来有效地识别异常值。然而,图5.4中没有这种全局相关方向。
当数据沿着低维的轴-平行子空间的簇自然对齐时,轴-平行子空间方法可以很好地发现异常值。但是,在图5.4中,其中的数据是沿任意相关方向对齐,这种情况下,轴-平行子空间方法无法有效工作。
广义子空间分析的目标是结合上面两种算法的思想。
即,发现异常值的同时还要确定任意定向子空间。
3.2 广义投影聚类方法
“广义”通俗来讲就是数据是任意定向的。在广义投影聚类方法中,聚类是在数据的任意对齐子空间中识别的,以确定除了集群之外的异常值。显然,异常值就是和集群不一致的数据。
使用该方法的主要目的是确定集群,在查找异常值方法不是特别高效。
该方法有时可能发现的是弱异常值,即噪声数据。
对于如何正确区分弱异常值(噪声数据)和强异常值(真正的异常),最简单的方法是计算每个候选离群点到每个聚类质心的局部马氏距离。
3.3 利用特定实例参考集
为了确定针对特定数据点的局部性进行优化的异常值,关键是确定针对正在评分的候选数据点X进行优化的局部子空间。
这种子空间的确定是不平凡的,因为通常不能从数据的局部聚集属性中推断出它,以检测罕见实例的行为。
最近提出了一种使用参考集在广义子空间中寻找异常值的方法。与较早的广义子空间聚类方法的主要区别在于,局部参考集特定于各个数据点,而聚类提供了一组固定的参考集,用于对所有点进行评分。这种灵活性的代价是,找到每个点特定参考集的运行时间为O(N),因此该方法需要O(N^2)时间进行评分。
3.4 旋转子空间采样(旋转袋)
旋转子空间采样是一种集成方法,它改善了特征袋。这种方法也成为旋转袋。
特征袋是为了发现轴-平行子空间中的异常值,旋转袋是为了发现广义子空间中的异常值。
因为旋转袋是一种集成方法,因此可以使用任何现成的异常检测算法(如LOF)作为基检测器。
旋转袋的基本思想:
旋转袋的基本思想是在低维空间中对随机旋转的子空间进行采样,并在这个低维空间中对每个点进行评分。各个子空间的分数可以组合起来。该方法使用维数为 r =2+ (√ d/2) 的子空间,这比特征袋中使用的子空间的典型维数低得多。这是因为旋转袋运行不同程度地从所有维度捕获信息。这也有助于获取多样性的子空间,从而提高整体得分的质量。
旋转袋算法流程:
1. 确定数据中随机旋转的轴系统
2.从旋转轴系统中采样r=2+(√ d/2) 方向。沿着r个方向投影数据。(r个随机旋转轴需要相互正交,就像在PCA中一样。)
3.在投影数据上运行基离群值检测器以及存储每个数据点的异常值分数。
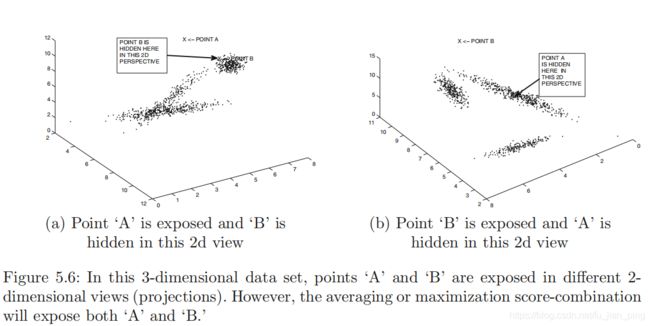
获取了每个点的不同预测的分数后,可以使用平均或最大值进行组合最后分数。
如上图5.6所示,通过综合两个试图,可以通过平均或最大值获取A和B的最后分数。
这个例子也说明集成方法如何克服单个检测器中的表示偏差,以便提高一个更通用的模型。这也是集成学习的内容。
3.5 非线性子空间
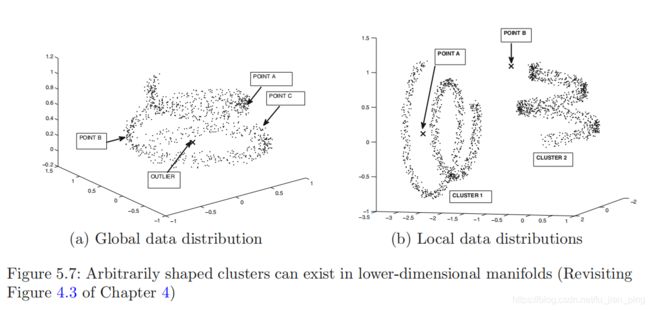
子空间异常检测最艰难的情况是数据流形存在于任意形状的低维子空间中。如下图5.7所示。
从上图可以看到,任意形状的簇可以存在于低维数据流形中。
面对上面这种情况,需要使用适当的局部非线性变换。这种提取是使用谱方法/谱嵌入(Spectral methods)实现的,也可以看作是一类特殊的核方法(其专门针对非线性的情况),它对发现任意形状的簇是比较有效的。
在这里,谱嵌入和K近邻检测器组合使用。
3.6 回归建模技术
可以使用回归模型进行子空间异常检测,方法是识别违反属性依赖性的点。
基本思想是将一个 d 维无监督异常检测问题分解为一组 d 回归建模问题。
我们可以使用现成的回归模型预测剩余的 (d-1) 个属性的每个属性。对于每个实例,汇总预测各种属性的评分误差以创建异常值分数。
4.子空间方法的探讨
高维异常检测分析的困难的主要原因是一些维数的局部噪声和无关性质的掩盖效应,这也往往表现为在距离上的集中。即在高维稀疏数据中,正常数据和异常数据的距离非常难判断。
目前在文献中主要研究是局部特征相关和距离集中这两个方面。
局部无关属性:
因此,通过使用全维距离度量,很难有效地确定异常值,因为噪声和无关维度的平均行为。此外,不可能先验地修剪特定的特征,因为不同的点可能显示不同类型的异常模式,每个模式使用不同的特征或视图 。
正是因为高维数据中全维特征选择的无效性,导致了局部特征选择或局部降维方法。
噪声和无关属性更有可能导致距离的集中。
异常值通常是由少量维度的行为来定义的。
有许多高维数据集,其中一个可以通过更简单的全维算法执行有效的孤立点检测。 特定算法在全维数据集上的有效性取决于应用场景和提取特征的方式。 如果在提取特征时考虑到特定的异常检测场景,那么全维算法可能会很好地工作。 尽管如此,子空间分析往往会发现异常值,而这些异常值不容易被其他全维算法发现。
事实上,子空间分析不应该被看作是一种独立的方法,而应该被看作是一种集成方法,以提高各种类型的基探测器的性能。
无论是开发一种用于高维孤立点检测的特定基础方法(如子空间直方图),还是将其封装在现有检测器(如特征和旋转套袋)上,将这一原理纳入孤立点检测中都有明显的好处。 此外,子空间分析提供了关于异常因果关系的有用见解;人们可以使用相关的局部子空间来提取对相关特征的特定组合的理解。
当异常值存在于少量局部相关维度时,子空间分析尤其有效。
在设计子空间方法时需要记住以下原则:
1、直接探索稀有区域是可能的,尽管由于组合爆炸,它在计算上具有挑战性
2、基于聚合的方法只提供有关子空间的弱提示。 这些方法的主要力量仅在于通过将来自不同子空间的结果组合在一起的中心设置。
3、集成的组成部分的设计应考虑到效率因素。 这是因为有效的组件能够实际使用更多的组件以获得更好的精度。
一个有趣的观察是,即使使用弱基探测器,组合它们往往会产生非常强的结果(三个臭皮匠,赛过诸葛亮)。 特征袋、子空间直方图和旋转袋等方法的成功是基于这一事实。 请注意,在每种情况下,底层基检测器不是特别强;但最终的离群点检测结果是非常有效的。 在高维孤立点检测和集成分析领域的最新进展是非常重要的。 尽管取得了这些进展,许多高维数据集仍然是孤立点分析的挑战。
5.总结
子空间方法用于异常检测的情况下,一个数据点的异常倾向被大量局部非信息维度的噪声效应稀释。 在这种情况下,通过搜索数据点明显偏离正常行为的子空间,可以显著地锐化异常分析过程。 最成功的方法为候选离群点识别多个相关子空间,然后将来自不同子空间的结果组合起来,以创建一个更健壮的基于集成的排序。