Tensorflow2学习笔记:房价预测
Tensorflow2学习笔记:房价预测
-
- 相关介绍
- 实验环境
- 实验步骤
-
- 导入相关库
- 获取数据
- 数据清洗
- 拆分训练数据集和测试数据集
- 数据检查
- 从标签中分离特征
- 数据规范化
- 模型
-
- 构建模型
- 检查模型
- 训练模型
- 进行预测
- 小结
- 参考文献
相关介绍
- Python是一种跨平台的计算机程序设计语言。是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。最初被设计用于编写自动化脚本(shell),随着版本的不断更新和语言新功能的添加,越多被用于独立的、大型项目的开发。
- TensorFlow 是一个端到端开源机器学习平台。它拥有一个全面而灵活的生态系统,其中包含各种工具、库和社区资源,可助力研究人员推动先进机器学习技术的发展,并使开发者能够轻松地构建和部署由机器学习提供支持的应用。
- Matplotlib是一个综合库,用于在Python中创建静态,动画和交互式可视化。
- Pandas是一个Python软件包,提供快速,灵活和可表达的数据结构,旨在使结构化(表格,多维,潜在异构)和时间序列数据的处理既简单又直观。
- Seaborn是基于matplotlib的图形可视化python包。它提供了一种高度交互式界面,便于用户能够做出各种有吸引力的统计图表。
- 房价预测是一个回归问题,本文通过以深圳房价数据集为例,旨在学习基本回归的思路!
实验环境
- Python 3.6.2
- Tensorflow-gpu 2.0.0
- Matplotlib 3.3.2
- Pandas 0.23.4
- Seaborn 0.11.0
实验步骤
导入相关库
import pathlib
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
获取数据
使用 pandas 导入数据集。
raw_dataset = pd.read_csv("shenzhen_house_price.csv")
dataset = raw_dataset.copy()
dataset.tail() # 查看末尾5行
| district | roomnum | hall | AREA | C_floor | floor_num | school | subway | per_price | |
|---|---|---|---|---|---|---|---|---|---|
| 18509 | longgang | 6 | 2 | 269.22 | middle | 10 | 1 | 1 | 9.2861 |
| 18510 | nanshan | 4 | 1 | 203.00 | low | 11 | 1 | 1 | 10.3448 |
| 18511 | pingshan | 3 | 2 | 88.08 | middle | 32 | 1 | 0 | 3.4060 |
| 18512 | longgang | 3 | 2 | 87.50 | middle | 33 | 1 | 1 | 6.6057 |
| 18513 | luohu | 3 | 2 | 69.30 | middle | 26 | 1 | 0 | 6.2771 |
数据清洗
# 统计每列nan值的个数
dataset.isna().sum()
district 0
roomnum 0
hall 0
AREA 0
C_floor 0
floor_num 0
school 0
subway 0
per_price 0
dtype: int64
# 序列特征映射
district_mapping = {'baoan': 0,
'dapengxinqu': 1,
'futian': 2,
'guangming': 3,
'longgang': 4,
'longhua': 5,
'luohu': 7,
'nanshan': 8,
'pingshan': 9,
'yantian': 10}
dataset['district']=dataset['district'].map(district_mapping)
C_floor_mapping = {'low': 0, 'middle': 1, 'high': 2}
dataset['C_floor']=dataset['C_floor'].map(C_floor_mapping)
dataset.tail() # 查看末尾5行
| district | roomnum | hall | AREA | C_floor | floor_num | school | subway | per_price | |
|---|---|---|---|---|---|---|---|---|---|
| 18509 | 4 | 6 | 2 | 269.22 | 1 | 10 | 1 | 1 | 9.2861 |
| 18510 | 8 | 4 | 1 | 203.00 | 0 | 11 | 1 | 1 | 10.3448 |
| 18511 | 9 | 3 | 2 | 88.08 | 1 | 32 | 1 | 0 | 3.4060 |
| 18512 | 4 | 3 | 2 | 87.50 | 1 | 33 | 1 | 1 | 6.6057 |
| 18513 | 7 | 3 | 2 | 69.30 | 1 | 26 | 1 | 0 | 6.2771 |
拆分训练数据集和测试数据集
将数据集拆分为一个训练数据集和一个测试数据集。最后将使用测试数据集对模型进行评估。
train_dataset = dataset.sample(frac=0.8,random_state=0) # frac=0.8,就是抽取其中80%
test_dataset = dataset.drop(train_dataset.index)
数据检查
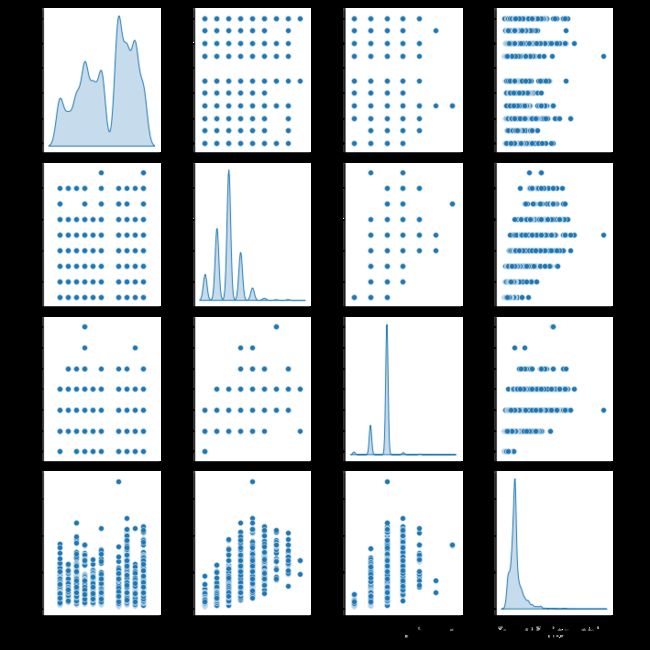
核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数,属于非参数检验方法之一
查看训练集中几对列的联合分布。
# 通过diag_kind='kde’显示双变量间的核密度并用其估计其特征
sns.pairplot(train_dataset[["district", "roomnum","hall","AREA"]], diag_kind="kde")
查看总体的数据统计
train_stats = train_dataset.describe()
train_stats.pop("per_price") # pop() 函数用于移除列表中的一个元素(默认最后一个元素),并且返回该元素的值
train_stats = train_stats.transpose() # 转置
train_stats
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| district | 14811.0 | 5.692526 | 3.015980 | 0.0 | 3.00 | 7.0 | 8.0 | 10.0 |
| roomnum | 14811.0 | 2.870299 | 1.047548 | 1.0 | 2.00 | 3.0 | 3.0 | 9.0 |
| hall | 14811.0 | 1.811356 | 0.487863 | 0.0 | 2.00 | 2.0 | 2.0 | 6.0 |
| AREA | 14811.0 | 95.052092 | 48.526370 | 15.0 | 70.52 | 88.0 | 103.2 | 697.2 |
| C_floor | 14811.0 | 1.022011 | 0.768946 | 0.0 | 0.00 | 1.0 | 2.0 | 2.0 |
| floor_num | 14811.0 | 27.519546 | 10.093864 | 1.0 | 23.00 | 31.0 | 33.0 | 90.0 |
| school | 14811.0 | 0.585241 | 0.492697 | 0.0 | 0.00 | 1.0 | 1.0 | 1.0 |
| subway | 14811.0 | 0.501722 | 0.500014 | 0.0 | 0.00 | 1.0 | 1.0 | 1.0 |
从标签中分离特征
将特征值从目标值或者"标签"中分离。 这个标签是你使用训练模型进行预测的值。
train_labels = train_dataset.pop('per_price')
test_labels = test_dataset.pop('per_price')
数据规范化
再次审视下上面的 train_stats 部分,并注意每个特征的范围有什么不同。
使用不同的尺度和范围对特征归一化是好的实践。尽管模型可能在没有特征归一化的情况下收敛,它会使得模型训练更加复杂,并会造成生成的模型依赖输入所使用的单位选择。
注意:尽管我们仅仅从训练集中有意生成这些统计数据,但是这些统计信息也会用于归一化的测试数据集。我们需要这样做,将测试数据集放入到与已经训练过的模型相同的分布中。
在此我们使用,零-均值规范化也称标准差标准化,经过处理的数据的均值为0,标准差为1。转化公式为:![]()
其中 μ \mu μ为原始数据的均值, σ \sigma σ为原始数据的标准差,是当前用得最多的数据标准化方式。
标准差分数可以回答这样一个问题:"给定数据距离其均值多少个标准差"的问题:
- 在均值之上的数据会得到一个正的标准化分数,反之会得到一个负的标准化分数。
# #归一化
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
模型
构建模型
这里,我们将会使用一个“顺序”模型,其中包含两个紧密相连的隐藏层,以及返回单个、连续值得输出层。模型的构建步骤包含于一个名叫 ‘build_model’ 的函数中,稍后我们将会创建第二个模型。 两个密集连接的隐藏层。
激活函数:
- 线性整流函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激活函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。
- 其图像如下:
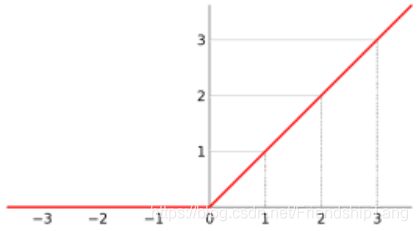
- 优势:
- 更加有效率的梯度下降以及反向传播,避免了梯度爆炸和梯度消失问题;
- 简化计算过程:没有了其他复杂激活函数中诸如指数函数的影响;同时活跃度-的分散性使得神经网络整体计算成本下降。
损失函数:
- 机器学习多数算法都需要最大化或最小化一个函数,即“目标函数”。一般把最小化的一类函数称为“损失函数”。
- 损失函数用于模型构建中,所以它用于指导模型的生成。
评估指标:
- 评估机器学习算法模型,有些问题中损失函数可以直接作为评价指标。
- 评估指标用于模型构建后,所以它用于评价模型性能。
在此回归问题中,均方误差(MSE)既用来指导模型构建,也用来在模型完成后评估模型性能
def build_model():
model = keras.Sequential([
layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
layers.Dense(64, activation='relu'),
layers.Dense(1)
])
optimizer = tf.keras.optimizers.RMSprop(0.001) # learning_rate=0.001
model.compile(loss='mse',# 损失函数
optimizer=optimizer, # 优化器
metrics=['mae', 'mse'] # 评估指标
)
return model
model = build_model()
检查模型
使用 .summary 方法来打印该模型的简单描述。
model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_9 (Dense) (None, 64) 576
_________________________________________________________________
dense_10 (Dense) (None, 64) 4160
_________________________________________________________________
dense_11 (Dense) (None, 1) 65
=================================================================
Total params: 4,801
Trainable params: 4,801
Non-trainable params: 0
_________________________________________________________________
试用下这个模型。从训练数据中批量获取‘10’条例子并对这些例子调用 model.predict
example_batch = normed_train_data[:10]
example_result = model.predict(example_batch)
example_result
array([[ 0.12918985],
[ 0.1756232 ],
[ 0.23027313],
[ 0.16373649],
[ 0.01900654],
[ 0.28642148],
[-0.26140502],
[ 0.15351082],
[ 0.19139563],
[ 0.23934828]], dtype=float32)
训练模型
对模型进行1000个周期的训练,并在 history 对象中记录训练和验证的准确性。
# 通过为每个完成的时期打印一个点来显示训练进度
class PrintDot(keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs):
if epoch % 100 == 0:
print('')
print('.', end='')
EPOCHS = 1000
# 训练模型
history = model.fit(
normed_train_data, # 训练数据
train_labels, # 训练标签
epochs=EPOCHS, # 训练周期
validation_split = 0.2, # 用作验证集的训练数据的比例。
verbose=0, # 日志显示模式。 0 = 安静模式, 1 = 进度条, 2 = 每轮一行。
callbacks=[PrintDot()] # 回调函数,用于在模型训练期间指定阶段被调用的函数
)
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
....................................................................................................
使用 history 对象中存储的统计信息可视化模型的训练进度。
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
| loss | mae | mse | val_loss | val_mae | val_mse | epoch | |
|---|---|---|---|---|---|---|---|
| 995 | 1.754809 | 0.881673 | 1.754809 | 3.012332 | 1.098387 | 3.012332 | 995 |
| 996 | 1.746673 | 0.877518 | 1.746674 | 3.533036 | 1.214398 | 3.533037 | 996 |
| 997 | 1.767880 | 0.884328 | 1.767881 | 3.020478 | 1.115132 | 3.020477 | 997 |
| 998 | 1.760693 | 0.885182 | 1.760694 | 3.260231 | 1.178415 | 3.260231 | 998 |
| 999 | 1.760055 | 0.888085 | 1.760056 | 3.035253 | 1.109489 | 3.035254 | 999 |
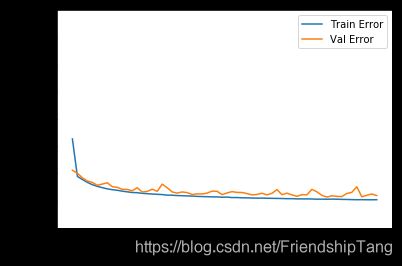
可视化训练误差和验证误差
def plot_history(history):
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Abs Error [per_price]')
plt.plot(hist['epoch'], hist['mae'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mae'],
label = 'Val Error')
plt.ylim([0,5])
plt.legend()
plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Mean Square Error [${(per\_price)}^2$]')
plt.plot(hist['epoch'], hist['mse'],
label='Train Error')
plt.plot(hist['epoch'], hist['val_mse'],
label = 'Val Error')
plt.ylim([0,20])
plt.legend()
plt.show()
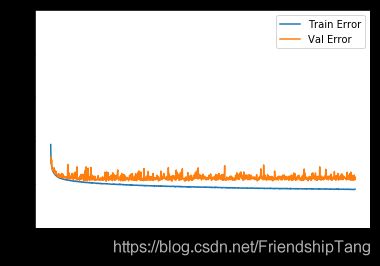
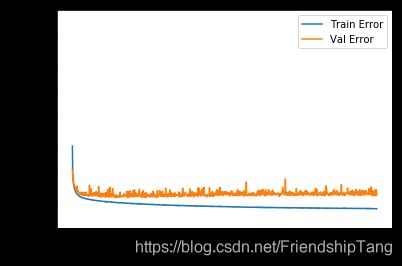
plot_history(history)
该图表显示在约10个 epochs 之后误差非但没有改进,反而出现恶化。
让我们更新 model.fit 调用,当验证值没有提高上是自动停止训练。
我们将使用一个 EarlyStopping callback 来测试每个 epoch 的训练条件。
如果经过一定数量的 epochs 后没有改进,则自动停止训练。
EarlyStopping是什么?
- EarlyStopping是Callbacks的一种,callbacks用于指定在每个epoch开始和结束的时候进行哪种特定操作。
- Callbacks中有一些设置好的接口,可以直接使用,如’acc’,’val_acc’,’loss’和’val_loss’等等。
- EarlyStopping则是用于提前停止训练的callbacks。
- 具体地,可以达到当训练集上的loss不在减小(即减小的程度小于某个阈值)的时候停止继续训练。
为什么要用EarlyStopping?
- 根本原因就是因为继续训练会导致测试集上的准确率下降。
- 那继续训练导致测试准确率下降的原因可能是:
- 过拟合
- 学习率过大导致不收敛
- 使用正则项的时候,Loss的减少可能不是因为准确率增加导致的,而是因为权重大小的降低。
当然使用EarlyStopping也可以加快学习的速度,提高调参效率。
model = build_model()
# patience 值用来检查改进 epochs 的数量
# patience:能够容忍多少个epoch内都没有改善。这个设置其实是在抖动和真正的准确率下降之间做权衡。
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', # 监控的数据接口,有'acc','val_acc','loss','val_loss'等等
patience=10)
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])
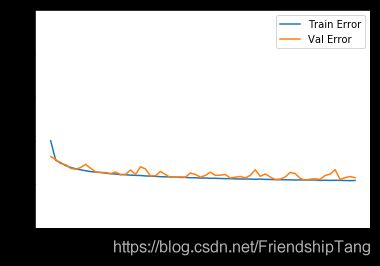
plot_history(history)
..............................................................
如图所示,验证集中的平均的误差通常在 +/- 1.0 pre_price左右。
通过使用 测试集 来泛化模型的效果如何,在训练模型时没有使用测试集。当我们在现实世界中使用这个模型时,我们可以期望它预测得有多好。
loss, mae, mse = model.evaluate(normed_test_data, test_labels, verbose=2)
print("Testing set Mean Abs Error: {:5.2f} per_price".format(mae))
3703/3703 - 0s - loss: 3.1772 - mae: 1.1967 - mse: 3.1772
Testing set Mean Abs Error: 1.20 per_price
进行预测
最后,使用测试集中的数据预测 per_price 值:
test_predictions = model.predict(normed_test_data).flatten()
plt.scatter(test_labels, test_predictions)
plt.xlabel('True Values [per_price]')
plt.ylabel('Predictions [per_price]')
plt.axis('equal') # x,y轴刻度等长
plt.axis('square') # 作图为正方形,并且x,y轴范围相同
plt.xlim([0,plt.xlim()[1]])
plt.ylim([0,plt.ylim()[1]])
_ = plt.plot([-100, 100], [-100, 100])
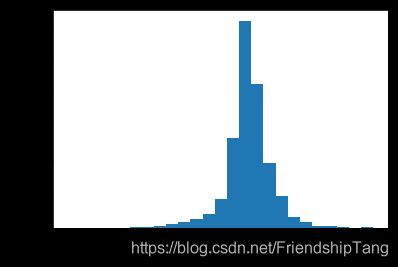
error = test_predictions - test_labels
plt.hist(error, bins = 25)
plt.xlabel("Prediction Error [per_price]")
_ = plt.ylabel("Count")
它不是完全的高斯分布,可能这是因为样本的数量很小所导致的。理论上,样本的数量足够大,即服从高斯分布(正态分布)。
小结
- 均方误差(MSE)是用于回归问题的常见损失函数。
- 用于回归的评估指标与分类不同。 常见的回归指标是平均绝对误差(MAE)和均方误差(MSE)。
- 当数字输入数据特征的值存在不同范围时,每个特征应独立缩放到相同范围,即归一化。
- 如果训练数据不多,一种方法是选择隐藏层较少的小网络,以避免过度拟合。
- 早期停止(EarlyStopping)是一种防止过度拟合的有效技术。
参考文献
[1]Tensorflow官方文档(https://tensorflow.google.cn/tutorials)