StyleGAN3 笔记
StyleGAN3
《Alias-Free Generative Adversarial Networks》
主页:https://nvlabs.github.io/stylegan3
论文:https://arxiv.org/abs/2106.12423
项目:https://github.com/NVlabs/stylegan3
从零带你入门stylegan~stylegan3的技术细节_Ericam_的博客-CSDN博客_stylegan
StyleGAN3论文解读
【论文解析】StyleGAN3 - Alias-Free Generative Adversarial Networks_门被核桃夹了还能补脑嘛的博客-CSDN博客_stylegan3论文
(哇很难受,他这个离散核的符号怎么都打不出来,他到底是怎么弄的啊,只能稍微拼了个替代品出来,不过看着还挺像的,无所谓了)
这篇完全就是突破性进展,解决了纹理粘连问题,这个问题真的广泛存在太久了。
但是很奇怪,即使是现在,也有好多新的论文仍然是基于StyleGAN2的,不知道为啥他们不用新的。
其实核心思路很简单,纹理粘连问题的根本原因是,卷积产生了额外的特殊分布的噪声,这些噪声分布与像素坐标高度相关,导致对后续层提供了额外的坐标信息,导致后续层产生了坐标依赖。
其实这种额外噪声我们都见过,棋盘格伪影就是其中一种表现形式。众所周知,这种周期性的噪声只要滤波就能去除,所以他们也是这么做的,他们给每一层之间都加滤波,保证每一层都不会产生对坐标信息的依赖(因为坐标信息已经被滤掉了)
当然了,padding和输入噪声图都会产生坐标信息,所以他们也想办法规避掉了。
padding是罪魁祸首完全可以理解,但是为什么说噪声图也会产生坐标信息?有可能是因为,虽然说是随机的,但是每个patch之间往往是不同的,这样经过几层处理之后就很有可能建立起像素坐标系。
也不对,我觉得只要做好滤波,并且平移和旋转时将所有噪声图跟着一起动,应该就完全不会有问题。(除非低分辨率的噪声图和高分辨率的噪声图无论怎么滤波都没法和谐的平移和旋转)
StyleGAN2为网络提供一个固定的初始噪声,我认为这就是人为提供一个坐标信息,希望能借此压制网络对额外噪声产生的依赖。不过显然这样不会比滤波的方案更好。
还发现一个很有意思的点, StyleGAN3-R 的结构,和 深度可分离卷积 其实非常像,都是1x1卷积配下采样卷积,而且下采样卷积也都没有通道间的通路,只不过 StyleGAN3-R 的下采样卷积核是不可训练的,只训练1x1卷积核。
纹理粘连
通过实验,认为这些问题出现的原因是:
- 使用图像边界参考(例如padding的使用实际上提示了图像的边界位置信息)
- 像素的噪声输入(本意是防止头发丝粘一起)
- 位置编码和混叠(加入一些额外的位置信息)。
如何消除这些不需要的辅助信息,从而防止网络去组合、使用这些错误信息呢?
-
针对边界问题,可以在稍大一点的图像边缘上进行操作。
-
针对像素的噪声输入,可以直接取消掉该操作。
-
而关于生成图像中的混叠,作者认为有两个可能的来源:
- 非理想上采样(如最近邻、双线性或 strided 卷积)产生的像素网格的微弱的印记。
- point-wise 的非线性激活,如 ReLU 或者 Swish。
网络会去放大哪怕是最轻微的混叠,并在多个尺度上进行组合,这就成为了固定在图像坐标中的那些混叠状网格的基础(解释了为何特征会依赖于坐标)。
而实验表明,在stylegan2时,当前的上采样滤波器在抑制混叠方面根本不够激进,而且需要具有超过100dB衰减的高质量滤波器。
而针对这个问题,stylegan3根据它们在连续域的影响,提出了一种解决点态非线性引起的混叠的理论,并对结果进行了适当的低通滤波。
他们表明,在解决了混叠问题后,基于 1*1 卷积的模型能产生一个强大的、具有旋转不变性的生成器
在足够压制混叠之后,网络的内部特征图会自然地浮现一种附着在表面的坐标系
相关工作
-
混叠似乎在深度学习中非常常见,是个老问题了
混叠产生的坐标网格,存在于深度学习[69, 59]中常用的所有滤波器,甚至是图像处理中使用的高质量滤波器。
有很多最近的工作研究了卷积网络中平移不变的缺失,主要是在分类背景下 [28, 35, 66, 5, 38, 69, 12, 71, 59]
在本文中作者显著地扩展了现有的抗混叠(抗锯齿)策略
群等变CNN旨在把平移权重共享带来的效率优势推广到旋转和缩放
作者的 1*1 卷积可以看作对 连续E(2)等变模型 [62] 的实现
Dey et al. [17] 将 90度旋转与翻转等变CNN [16] 引入了 GAN ,提升了数据高效性。作者的工作与他们的是互补的,但作者不是为了高效性。
最近的基于 隐含网络 [53, 56, 13] 的 GAN [4, 54] 使用类似的 1*1 卷积。虽然是等变的,但是这些模型并没有解决纹理粘连问题,因为他们并没有层次化地使用上采样,也没有实现浅层的抗混叠上采样。
使用连续信号解释等变性
我们不能直接把信号看作是储存在像素阵列中的数值,这会使我们无法考虑到半像素。
根据奈奎斯特-香农采样定理,一个频率为 f f f 的周期采样信号可以表示频率在 [ 0 , f / 2 ] [0,f/2] [0,f/2] 范围内的任意连续信号。
根据香农插值算法,我们可以从离散信号中恢复出连续信号。方法是将 离散信号 和 理想的插值滤波器 进行卷积。
在用离散信号恢复连续信号的时候,仅仅使用我们画幅内的区域是不够的,因为区域外的离散信号也会影响恢复出的连续信号,
理论上我们需要存储一个无限大的离散信号图才行,
实践上,我们用了一个比感兴趣的区域稍微大一点的特征图
然后我们可以定义在连续域上工作的神经网络层与在离散域工作的神经网络层之间的转换方式
具有等变性的网络层
我们希望层具有两种等变性:平移和旋转
旋转等变性对谱有更强的约束,这要求
谱必须是半径为 s/2 的圆形(而且像光盘一样一圈一圈)
这适用于初始输入和降采样带通滤波器
我们只分析单通道特征图,因为特征图的 point-wise 的线性组合(其实就是1*1 卷积)对我们的分析没有影响
卷积
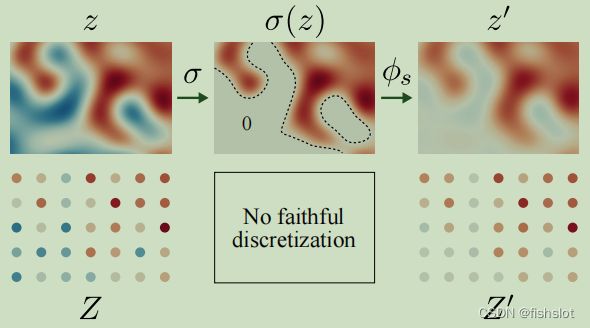
事实上,直接用离散核去卷 z ,和先把 z 离散化为 Z ,再和离散核卷积,再连续化,是一样的
这不会引入新的频率,所以自然满足了频带限制
卷积天然满足平移等变性
1*1 卷积可以满足旋转等变性
上采样
理想的上采样不应该改变连续信号,只是单纯的提高离散信号的采样率
连续版:
离散版:
离散版实现:
如果我们想把采样率放大 n 倍,只需要在 Z 里面插0 ,
然后用 I I I s ′ ⊙ ϕ s \def\W{\text {I\hspace{-0.1mm}I\hspace{-0.1mm}I}} \W_{s^{\prime}} \odot \phi_s IIIs′⊙ϕs 做卷积就行了(注意这是一个离散的卷积核)
下采样
下采样需要一个低通滤波器,这只需要一个简单的低通卷积就可以实现
连续版:
f down ( z ) = ψ s ′ ∗ z , 其中 ψ s : = s 2 ⋅ ϕ s \mathbf{f}_{\text {down }}(z)=\psi_{s^{\prime}} * z \ ,其中 \ \psi_{s}:=s^{2} \cdot \phi_{s} fdown (z)=ψs′∗z ,其中 ψs:=s2⋅ϕs
离散版:
F down ( Z ) = I I I s ′ ⊙ ( ψ s ′ ∗ ( ϕ s ∗ Z ) ) = 1 / s 2 ⋅ I I I s ′ ⊙ ( ψ s ′ ∗ ψ s ∗ Z ) = ( s ′ / s ) 2 ⋅ I I I s ′ ⊙ ( ϕ s ′ ∗ Z ) 用到了滤波器性质: ψ s ∗ ψ s ′ = ψ min ( s , s ′ ) \def\W{\text {I\hspace{-0.1mm}I\hspace{-0.1mm}I}} \begin{split} \mathbf{F}_{\text {down }}(Z) &=\W_{s^{\prime}} \odot (\psi_{s^{\prime}} * (\phi_{s} * Z)) \\ &=1/s^{2}\cdot\W_{s^{\prime}} \odot(\psi_{s^{\prime}}*\psi_{s}*Z) \\ &=(s^{\prime}/s)^{2} \cdot \W_{s^{\prime}} \odot (\phi_{s^{\prime}}*Z) \\\\ 用到了滤波器性质: &\psi_{s} * \psi_{s^{\prime}}=\psi_{\min (s, s^{\prime})} \end{split} Fdown (Z)用到了滤波器性质:=IIIs′⊙(ψs′∗(ϕs∗Z))=1/s2⋅IIIs′⊙(ψs′∗ψs∗Z)=(s′/s)2⋅IIIs′⊙(ϕs′∗Z)ψs∗ψs′=ψmin(s,s′)
离散版实现:
下采样整数倍,就是简单的丢掉一些点后做一个离散卷积
(他没说,但是我估计卷积核就是 ( s ′ / s ) 2 ⋅ I I I s ′ ⊙ ϕ s ′ \def\W{\text {I\hspace{-0.1mm}I\hspace{-0.1mm}I}} (s^{\prime}/s)^{2} \cdot \W_{s^{\prime}} \odot \phi_{s^{\prime}} (s′/s)2⋅IIIs′⊙ϕs′
平移等变性自动就有
旋转等变性需要 ϕ s ′ \phi_{s^{\prime}} ϕs′ 具有径向对称性、具有光盘形的频率响应
理想的滤波器定义如下:
ϕ s ∘ ( x ) = jinc ( s ∥ x ∥ ) = 2 J 1 ( π s ∥ x ∥ ) / ( π s ∥ x ∥ ) \phi_{s}^{\circ}(\boldsymbol{x})=\operatorname{jinc}(s\|\boldsymbol{x}\|)=2 J_{1}(\pi s\|\boldsymbol{x}\|) /(\pi s\|\boldsymbol{x}\|) ϕs∘(x)=jinc(s∥x∥)=2J1(πs∥x∥)/(πs∥x∥)
其中 J 1 J_1 J1 为第一类一阶 Bessel 函数 ( the first order Bessel function of the first kind )
非线性激活
在离散域中使用 point-wise 的激活函数并不能实现平移旋转等变性,
不过在连续域中,任何 point-wise 的函数都有平移旋转等变性
但是还需要考虑频带限制,在连续域中使用 ReLU 会引入高频信号,这无法在输出中表示出来。
一个自然的解决方案是用一个理想低通滤波器 ψ s \psi_{s} ψs 做卷积
连续版:
f σ ( z ) = ψ s ∗ σ ( z ) = s 2 ⋅ ϕ s ∗ σ ( z ) \mathbf{f}_{\sigma}(z)=\psi_{s} * \sigma(z)=s^{2} \cdot \phi_{s} * \sigma(z) fσ(z)=ψs∗σ(z)=s2⋅ϕs∗σ(z)
离散版:
F σ ( Z ) = s 2 ⋅ I I I s ⊙ ( ϕ s ∗ σ ( ϕ s ∗ Z ) ) \def\W{\text {I\hspace{-0.1mm}I\hspace{-0.1mm}I}} \mathbf{F}_{\sigma}(Z)=s^{2} \cdot \W_{s} \odot (\phi_{s} * \sigma(\phi_{s} * Z)) Fσ(Z)=s2⋅IIIs⊙(ϕs∗σ(ϕs∗Z))
离散版实现:
如果要实现离散版,就必须要把信号转换到连续域
为了近似实现这一点,先把信号上采样,在高分辨率上做非线性激活,再下采样
上采样的时候,作者发现只要 2 × 2\times 2× 的上采样就有足够高质量的等变性了
下采样的时候,记得下采样要用 ϕ s ∘ \phi_{s}^{\circ} ϕs∘
注意非线性激活是所有操作中唯一可能引入新频率的操作,并且我们可以在最终离散化之前,应用一个截止频率低于 s / 2 s/2 s/2 的重构滤波器来限制新频率的范围。这使得我们可以控制生成器的每一层引入了多少新信息。
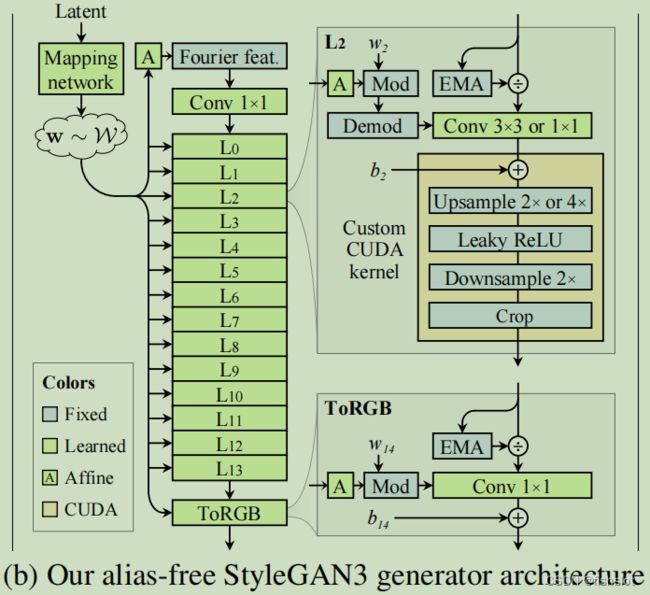
对 StyleGAN2 进行改进
设计了指标,来度量两种等变性,详见原文。
(B)傅立叶特征
将网络输入的常数替换为随机的傅立叶特征
从频域中半径为2的圆中均匀采样傅立叶特征,并且不参与优化
(C)去除输入噪声
去除了加在网络中间的 pixel-wise 的噪声
(D)简化网络
根据 Karras et al. [32] 的建议,减少了 mapping network 的深度
去除了混合正则化和感知路径正则化 [34] (混合正则化就是用两个 z 来生成)
去除了output 的残差连接
作者假设这些东西的好处主要与训练过程中的 gradient magnitude dynamics 有关,并在每次卷积之前使用 simple normalization 来直接解决根本问题。
simple normalization 就是在训练时记录所有像素和特征图的指数平均 σ 2 = E ( x 2 ) \sigma^2=E(x^2) σ2=E(x2) ,然后将特征图除以 σ 2 \sqrt{\sigma^2} σ2
实践中,直接把这次除法融入卷积核的权重里,来提高性能
(E)扩展边界
理论上我们需要无穷大的离散特征图才能够保留所有连续信号中的信息。为了近似这一点,在特征图外围延伸一个固定尺寸的边缘。这是必要的,因为寻常卷积中使用的 padding 会泄露边界信息 [28, 35, 66] 。
经过实验,确定边缘是 10 个像素,用更大的边缘没什么明显区别。
(E)上采样
把原本的双线性上采样替换为一个近似理想的低通滤波器。
使用一个 windowed sinc filter with a relatively large Kaiser window [41] of size n = 6 ,
这意味着,在上采样中,每个输出像素都与6个输入像素有关,在下采样中,每个输入像素都影响 6 个输出像素。
Kaiser window 是一个特别好的选择,因为他能显式控制 过渡带和衰减。
在本节的剩余部分中,我们显式的指明过渡带,然后用 原始的Kaiser公式 计算剩余参数。(附录C)
目前,我们使用临界采样,设置滤波器的截止频率为 f c = s / 2 f_c=s/2 fc=s/2 ,即正好在 带限 和 过渡带半宽 f h = ( 2 − 1 ) ( s / 2 ) f_h=(\sqrt{2}-1)(s/2) fh=(2−1)(s/2) 处
回想一下,采样率 s 等于像素宽度。
在后续消融实验中(图3),更小的重采样滤波器 ( n=4 ) 会影响平移等变性,更大的滤波器 ( n=8 ) 主要是增加了训练时间,所以还是 n=6 比较好。
(F)带滤波的非线性激活
理论上我们需要把特征上采样 m 倍,做 LReLU ,再下采样 m 倍。
我们进一步发现,由于是带限信号,可以交换卷积和上采样的顺序,所以我们可以把 2 × 2\times 2× 上采样和后续的 m × m\times m× 上采样融合成一次 2 m × 2m\times 2m× 上采样。
实验发现 m=2 就够了。
自定义了 CUDA核 来实现 上采样-LReLU-下采样 的操作,使得训练速度加快了10倍,并且省了很多内存。
(G)非临界采样
临界采样(截止频率正好在带限上的滤波)在 反混叠 和 保留高频细节 中找到一个好的平衡。但是我们的目的是很不同的,混叠会严重影响生成器的等变性。高频细节在最高分辨率的图层中很重要,但是在早期的图层里就没那么重要了。
为了减少混叠,我们可以直接把截止频率 f c f_c fc 降到 f c = s / 2 − f h f_c=s/2-f_h fc=s/2−fh ,保证所有的混叠频率(高于s/2)都在 stopband 内。
(大概就是说,原来的滤波范围允许通过一半的过渡带信号,现在要完全把过渡带信号排除)
如图,如果降低图中蓝色滤波器的 f c f_c fc 会使其频率响应向左移动,使得最坏情况下,对混叠频率的衰减从 6dB 提高到 40dB 。
这种过采样行为可以看作是为了达到更好的抗混叠效果所付出的计算代价。
在实践中,我们在所有中使用更低的 f c f_c fc ,除了最高分辨率的层,因为要生成看起来清晰的图像,以符合训练集。
(H)带变换的傅里叶特征
如图,输入的傅里叶特征会经过一个由 w 控制的仿射变换,然后再输入网络。
这是为了让网络有能力使用 w 控制整体的平移和旋转,使得随机生成的图片的方向是有变化的。
(T)柔性的层规格(StyleGAN3-T)
我们发现仍然存在一些可见的伪影。
经过更仔细地检查,我们发现,这是因为,对最低分辨率的层,在(G)中定义的滤波器的衰减力度仍然不够。这些层往往有很多频率在带限附近,这就需要非常强的衰减,来完全消除混叠。
这张图展示了一个例子,一个14层生成器的滤波器参数递增图,其中最后两层是临界采样的全分辨率层。
(这段没看懂,应该就是大致描述了一下他们设计的频谱性质)
这个新的层规格再次提升了平移等变性,消除了剩余的伪影。
消融实验表示,可以通过调整 f t , 0 f_{t,0} ft,0 在训练速度和等变性质量之间做权衡。
注意,现在层数是一个自由参数,不取决于输出分辨率了。事实上,我们发现固定层数在多种分辨率下是一致的,并且使其他超参数(比如学习率)表现得更可预测。在本文的其余部分,我们使用14层。
(R)旋转等变性(StyleGAN3-R)
用了两个改动来达成旋转等变性。
首先,把 33 卷积换成了 11 卷积。为了弥补损失的模型容量,将特征图数量翻倍。现在只有上采样和下采样能在像素之间传递信息了。
其次,将 sinc-based 下采样滤波器 替换为 jinc-based 下采样滤波器,使用相同的 Kaiser 方案(附录C)。
除了最后两个临界采样层,所有的层都执行了上述替换。毕竟匹配训练数据中潜在的 non-radial 谱是很重要的。
我们还使用了一个技巧,用于稳定训练过程:在训练早期,将判别器看到的图像加一个高斯模糊。在前 200k 图片中, σ \sigma σ 逐渐从 10 减到 0 。
这是为了避免判别器在前期过于关注高频信息。