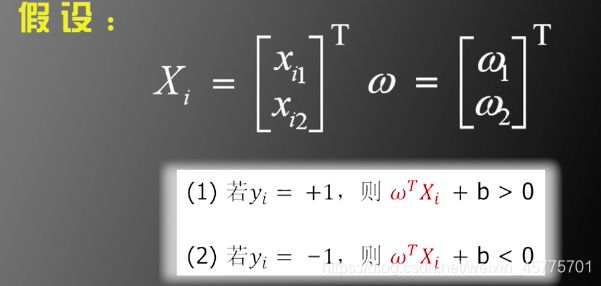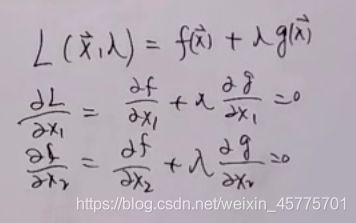《机器学习》周志华 第6章支持向量机。笔记+习题
裂开了呀，我高数都快忘完了
这章对我来说太难了！！！！！
非常感谢这个up主link.可以说是非常详细了。
公式推导可以参考link.
本章视频详细讲解link.
《机器学习实战》参考 link.
理解这章要做什么**
SVM性质：训练完成后，大部分训练样本不需要保留，最终模型仅与支持向量有关。
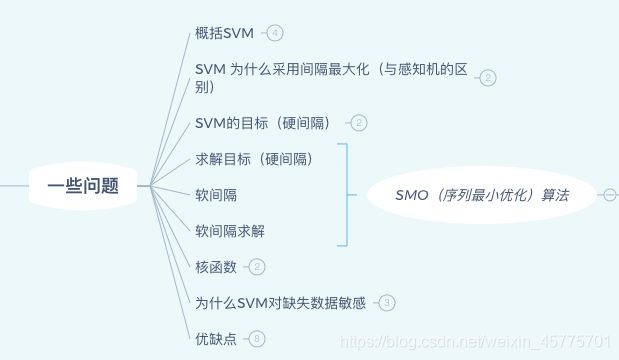
这是这章重点解决的问题。之后在本文末尾再详细概括。
6.1 间隔与支持向量
在样本空间中，用线性方程来表示划分超平面：ωTx + b = 0 ；其中ω = (ω1;ω2; … ; ωd)为法向量，决定超平面内的方向；b为位移项，决定超平面与原点之间的距离。
6.1.1前期准备
支持向量机和对率回归的优化目标接近：
①对率回归的优势在于其输出具有自然的概率意义，即在给出预测标记的同时也给出了概率；而支持向量机的输出不具有概率意义。
② 对率回归能直接用于多分类任务，支持向量机需要推广。
6.1.2模型
- 训练数据及标签
- 线性可分
数学形式
向量形式：
使间隔最大的超平面是如何取到的？
6.1.3支持向量机的优化
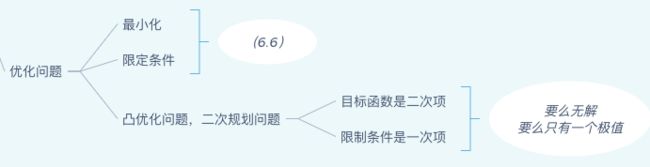
在式子（6.6）中，为了最大化d，我们可以重写为最小化minimize。乘以1/2，是为了求导的方便。
限制条件中 ，不等式的右边数字可以随便变，差的只是一个a而已。
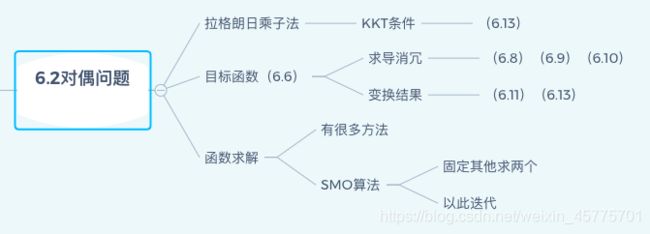
6.2对偶问题（这部分我快裂开了！！！）
可以看这个up主link.
或者link.
6.2.1拉格朗日乘子法
当限制条件是等式的情况下
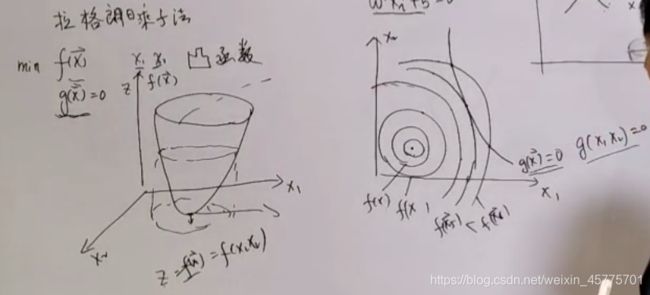
整个圆上，f()的值是相同的。
只有圆和曲线g()相切的时候，也就是f(x5)的地方，是满足限定条件的最小值。
可以看出，此时法线相同，梯度平行，如下图
所以可以得到
回到拉格朗日乘子法，存在新的λ，使
λ的值(正负数皆可能)
当限制条件是不等式的情况下
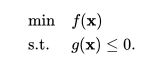
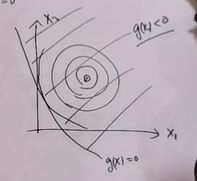
像上图这种情况，约束条件不起作用。
即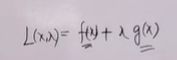
中λg(x)=0。所以要么λ=0（内部解），要么g(x)=0（边界解）
因此，不论是内部解或边界解，λg(x) 恒成立，称为互补松弛性(complementary slackness)。
所以KKT条件就出来了。
6.2.2目标函数转化
上式需满足KKT条件，即：（6.13）
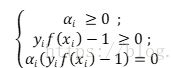
若αi = 0，则样本不会对f(x)产生影响；
若αi＞0，则必有yif(xi) = 1，对应的样本点位于最大间隔边界，是一个支持向量；
这表明SVM的一个重要性质：训练完成后，大部分训练样本不需要保留，最终模型仅与支持向量有关。
6.2.3函数求解（SMO算法）
SMO先选取违背KKT条件程度最大的变量，在选取第二个变量时，使选取的两变量所对应样本之间的间隔最大。
6.3核函数
对于原本样本空间不可分的分类问题，可将样本映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。
如果原始空间是有限维，即属性数有限，那么一定存在一个高维特征空间使样本可分
6.3.1非线性svm
- 把非线性转化为线性。 低维->高维
- 找出对应核函数。 高维->低维
6.3.2常用核函数
只要一个对称函数所对应的核矩阵是半正定的，它就能作为核函数使用；
常用的核函数：
优缺点
-
多项式核
在上一部分，非线性转化为线性中就用到了 多项式核 -
高斯核函数
如何选择核函数 -
当特征维数 d 超过样本数 m 时 (文本分类问题通常是这种情况), 使用线性核; 当特征维数 d 比较小. 样本数 m 中等时,
使用RBF核; 当特征维数 d 比较小. 样本数 m 特别大时, 支持向量机性能通常不如深度神经网络
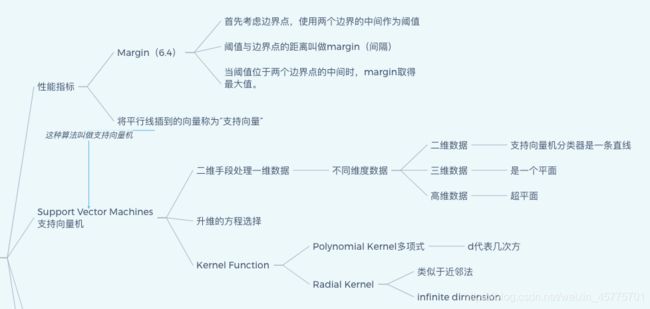
6.3.3核函数的性质
6.4软间隔与正则化
6.4.1软间隔
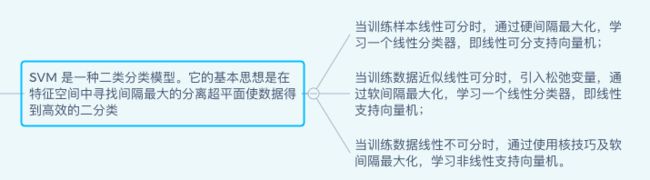
- 硬间隔：所有样本必须划分正确
- 软间隔：允许某些样本不满足约束
此时优化目标可以写为
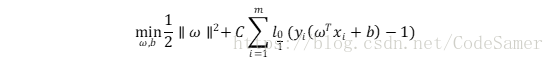
l0/1表示“0/1损失函数”：
由于l0/1的数学特性不太好，常用一些函数替代l0/1，称为替代函数；通常是凸函数且是l0/1的上届，常见的有hinge损失、指数损失、对率损失。
下图是用“松弛变量”代替损失函数：
软间隔支持向量机
6.4.2正则化
正则化可理解为一种“罚函数法”，即对不希望得到的结果施以惩罚，从而使得优化过程趋向于希望的目标。
6.5支持向量回归（Support Vector Regression）
1）SVR假设我们能容忍f(x)与y之间最多有ε的偏差，即晋档f(x)与y之间的差别绝对值大于ε时才计算损失；相当于以f(x)为中心构建一个宽度为2ε的间隔带。
（2）SVR问题形式化为：
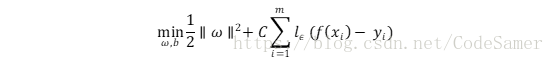
其中C为正则化常数，lε是ε-不敏感损失函数：
引入松弛变量
引入拉格朗日乘子
求偏导
得到对偶问题
最终SVR的解为：
能使上式中（αi’- αi）≠0的样本记为SVR的支持向量。
这时候，SVR的支持向量仅是训练样本的一部分，即其解仍具有稀疏性，这与SVM的模型只与支持向量有关不一样。
可以看到SVR的求导过程跟SVM的一模一样。
更具体的推导可以看链接: link.
6.6核方法
人们发展出一系列基于核函数的学习方法，统称为“核方法”
（1）表示定理（representer theorem）
（2）现实中，常通过“核化”（即引入核函数）来将线性学习器拓展为非线性学习器。
（3）支持向量机是针对二分类任务设计的，其求解通常是借助于凸优化技术，核函数直接决定了支持向量机与核方法的最终性能，替代损失函数在机器学习中被广泛应用。
总结
-
概括SVM
-
SVM 为什么采用间隔最大化（与感知机的区别）
-
SVM的目标（硬间隔）
使间隔最大化；使样本正确分类。 -
-
核函数
- 为什么SVM对缺失数据敏感
- 优缺点
习题
转载自https://www.cnblogs.com/cloud–/p/12304663.html
以及 link.
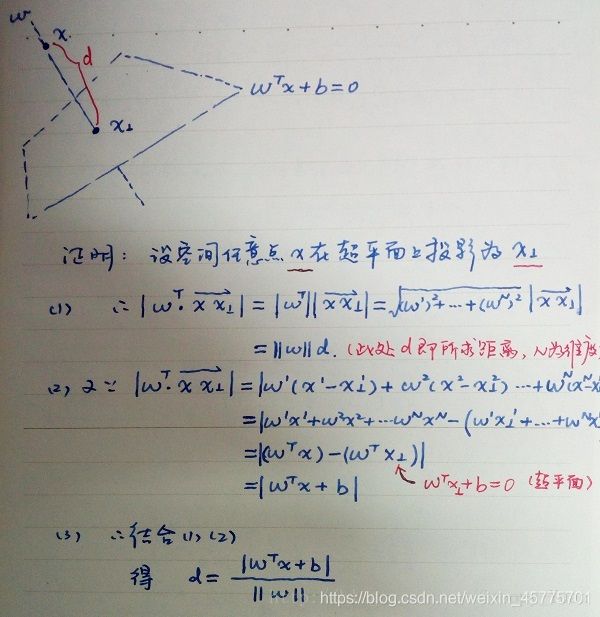
- 试 证 明 样 本 空 间 中 任 意 点 x 到 超 平 面 ) ( w , b ) 的 距 离 为 式 ( 6.2 ) 试证明样本空间中任意点 \bm{x} 到超平面 ) (\bm{w}, b) 的距离为式(6.2) 试证明样本空间中任意点x到超平面)(w,b)的距离为式(6.2)
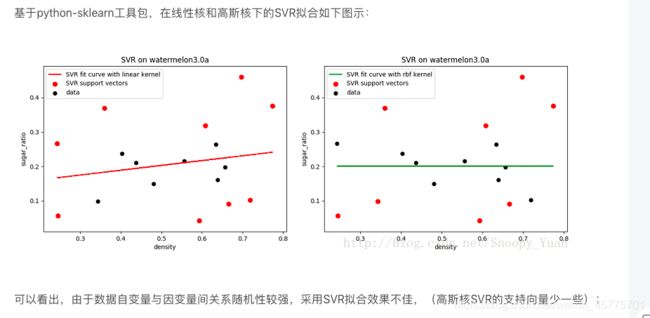
6.2 不同核函数对应的支持向量差别分析
2. 试 使 用 L I B S V M ， 在 西 瓜 数 据 集 3.0 α 上 分 别 用 线 性 核 和 高 斯 核 训 练 一 个 S V M ， 并 比 较 其 支 持 向 量 的 差 别 。 2.试使用LIBSVM，在西瓜数据集 3.0 \alpha 上分别用线性核和高斯核训练一个SVM，并比较其支持向量的差别。 2.试使用LIBSVM，在西瓜数据集3.0α上分别用线性核和高斯核训练一个SVM，并比较其支持向量的差别。
链接: link.
链接: link.
链接: link.
6.3 SVM与BP网络、C4.5决策树等的对比实验
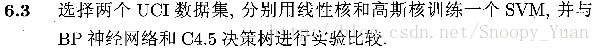
link.
link.
6.4 线性核SVM与LDA的关联
试讨论线性判别分析与线性核支持向量机在何种条件下等价.
线性判别分析能够解决n分类问题，而SVM只能解决二分类问题。如果要解决n分类问题只能通过OvR来迂回解决.
线性判别分析能将数据以同类样例间低方差和不同样例中心之间大间隔来投射到一条直线上, 但是如果样本线性不可分, 那么线性判别分析就不能有效进行, 支持向量机也是.
综上, 等价的条件是:
1。数据有且仅有 2 种, 也就是说问题是二分类问题.
2。数据是线性可分的.
实际上都利用了核技巧, 将原来的数据映射到一个更高维的空间使其变得线性可分.
SVM的决策边界（超平面）是由支持向量所确定的，即是利用相对较少的数据特征来学得整个数据的特性。由于支持向量相对较少，其上的噪声会对超平面的确定产生相对较大的影响。
反观对率回归, 其线性超平面由所有数据共同决定, 因此一点噪声并无法对决策平面造成太大影响.
参考书中附录公式B.3，KKT条件即拉格朗日函数在对参数进行偏导取0计算后，为求得最优解，乘子和约束必须满足其中之一为0的条件。
要获取式（6.52）的完整KKT条件，只需将式（6.47~6.50）代入该式即可。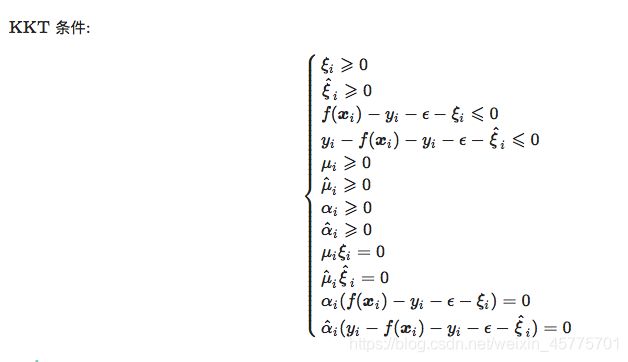
6.8 SVR实验
link.
或者
关于核对率回归（KLR），可参考书p132中关于 log 损失函数下SVM与LR的比较，也可参考台大林轩田-机器学习技法中关于KLR的slide。
简要说明如下：
或者参考link.
支持向量的规模与SVM计算速度息息相关，在不影响模型性能的情况下减少支持向量数目，能有效提高SVM效率。
可以将一些冗余的支持向量去除到只剩必要的支持向量. 比如在二维平面, 只需要 3个支持向量就可以表达一个支持向量机, 所以我们将支持向量去除到只剩 3个.
更广泛的情况是, 若是 n 维平面, 那么只需要 n+1 个支持向量就能表达一个支持向量机.