python-实现多元回归及预测
题目
1.实现一元(或多元)线性回归
a. 根据对客观现象的定性认识初步判断现象之间的相关性(略)
b. 绘制散点图
c. 进行回归分析,拟合出回归模型
d. 对回归模型进行检验—计算相关系数、异方差检验
e. 进行回归预测
代码
# -*- coding=utf-8 -*-
# name: nan chen
# date: 2021/5/6 15:05
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['KaiTi'] # 指定默认字体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 读取数据 进行数据预处理
def read_check_data():
data_before = pd.read_csv(r"D:\Downloads\GDP-DATA.csv", encoding='gbk')
# 输出每个列丢失值
total = data_before.isnull().sum().sort_values(ascending=False)
print(total)
data = data_before.drop(data_before[data_before['construction'].isnull()].index)
x_first = np.array(data['industrial'])
x_second = np.array(data['construction'])
x_third = np.array(data['transportation'])
x = range(1, len(x_first) + 1)
y_income = np.array(data['gdp'])
# 可视化展示数据
plt.title("1992年至今季度国内生产总值与工业、建筑业、交通运输业增加值(万亿元)")
plt.plot(x, x_first, '.', label='工业增加值')
plt.plot(x, x_second, '.', label='建筑业增加值')
plt.plot(x, x_third, '.', label='交通运输业增加值')
plt.plot(x, y_income, '.', label='国内生产总值')
plt.legend()
return x_first, x_second, x_third, y_income
# 多元线性回归
def multiple_regression(x_first, x_second, x_third, y_income):
x = range(1, len(x_first) + 1)
Y = y_income.T
X = np.array([list(x) for x in zip(np.ones(len(y_income)), x_first, x_second, x_third)])
B = np.matmul(np.matmul(np.linalg.inv(np.matmul(X.T, X)), X.T), Y)
print("B = ", B)
# 多元线性回归模型
print("回归方程为 y = %f + %fx1 + %fx2 + %fx3" % (B[0], B[1], B[2], B[3]))
y_predict = B[0] + B[1] * x_first + B[2] * x_second + B[3] * x_third
# 可视化
plt.figure()
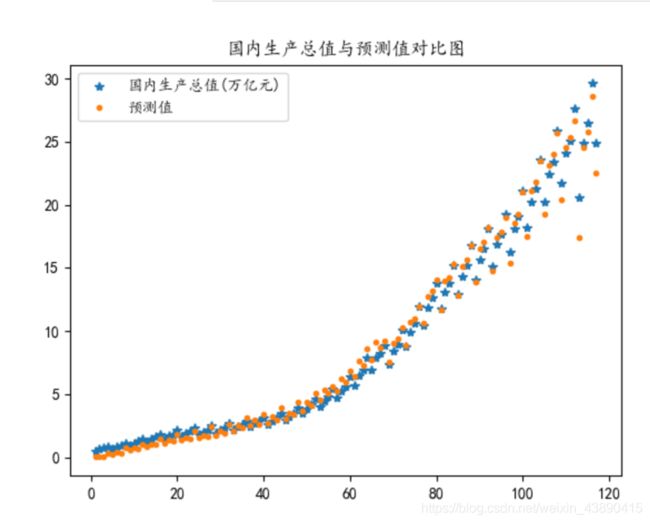
plt.title("国内生产总值与预测值对比图")
plt.plot(x, y_income, '*', label='国内生产总值(万亿元)')
plt.plot(x, y_predict, '.', label='预测值')
plt.legend()
return X, B, y_predict
# 检验
def check(y_real, y_predict, X, B):
y1 = np.sum((y_predict - np.mean(y_real)) ** 2)
y2 = np.sum((y_real - np.mean(y_real)) ** 2)
R1 = y1 / y2
print("可决系数R^2=", R1)
R2 = 1 - ((len(y_real) - 1) / (len(y_real) - 4 - 1)) * (1 - R1 ** 2)
print("修正自由度的可决系数R^2=", R2)
# 计算标准估计误差
S = (np.sum((y_real - y_predict) ** 2) / (len(y_real) - 4)) ** 0.5
print("标准估计误差为S = ", S)
u2 = (y_real - y_predict) ** 2
plt.figure()
plt.title("u^2-x散点图")
plt.plot(u2, '.')
plt.show()
S = (np.sum((y_real - y_predict) ** 2) / (len(y_predict) - 4)) ** 0.5
C = np.linalg.inv(np.matmul(X.T, X))
T = []
for i in range(len(B)):
T.append(B[i] / (S * C[i][i] ** 0.5))
print(T)
T = np.array(T)
plt.figure()
plt.axhline(y=1.9818, ls="-", c="green")
plt.plot(np.abs(T), '.')
plt.show()
print(y_predict[-1])
if __name__ == '__main__':
x_first, x_second, x_third, y_income = read_check_data()
X, B, y_predict = multiple_regression(x_first, x_second, x_third, y_income)
check(y_income, y_predict, X, B)
结果与分析
数据集分析:
本次实验从国家统计局找到了1992年至今每一季度的国内生产总值与与工业增加值、建筑业增加值、交通运输业增加值的数据。将国内生产总值作为被解释变量,工业增加值、建筑业增加值、交通运输业增加值作为解释变量。
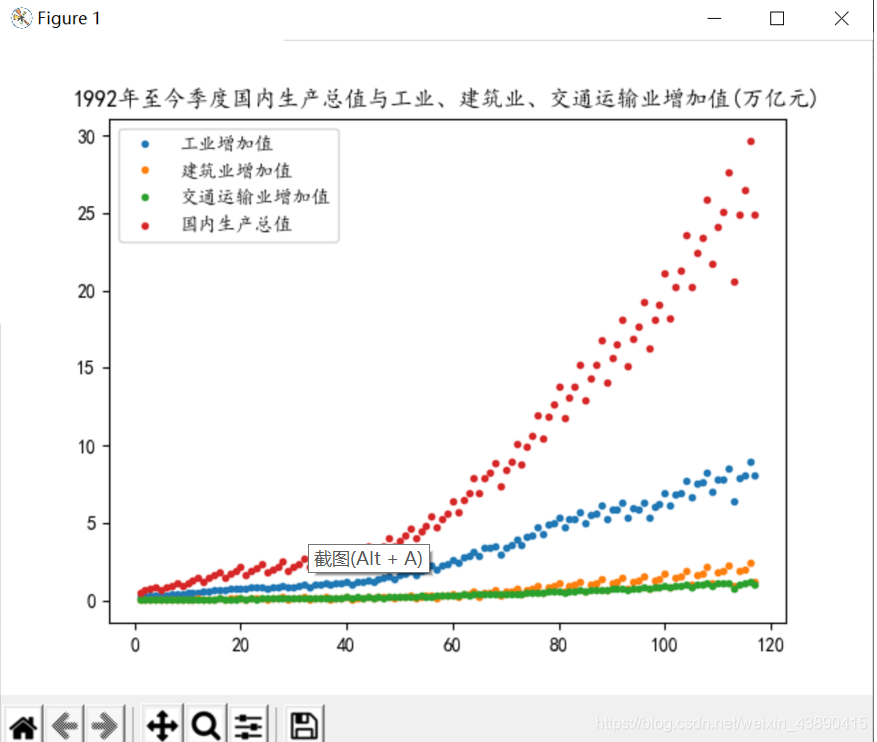
从图中可以看出,国内生产总值与工业增加值、建筑业增加值、交通运输业增加值呈现出较为一致的联动变化关系,均呈现向上增长的趋势。根据经济规律与现实经验,推测国内生产总值与工业增加值、建筑业增加值、交通运输业增加值存在线性相关关系。将用回归方程进行计算的国内生产总值预测值与国内生产总值的实际值进行对比,虽然有一些偏差,但是大题的走向是一致的,并且偏差不大。
多元线性回归
多元线性回归检验:
拟合优度检验
通过计算可决系数与修正自由度的可决系数进行多元线性回归方程的拟合优度检验

可以看出被解释变量国内生产总值与解释变量工业增加值、建筑业增加值、交通运输业增加值应该存在高度相关性,且该回归模型的拟合度较高。
回归系数显著性检验
查t分布表得t_(∝/2) (116-3-1)=1.9818
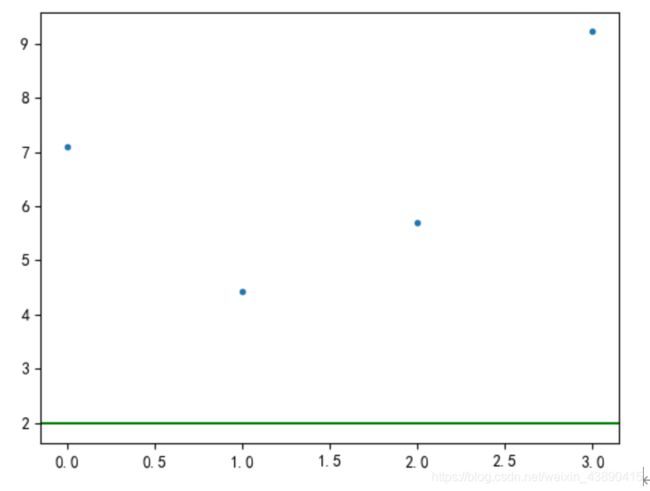
四个回归方程系数均大于t_(∝/2) (116-3-1),所以回归方程的系数均通过显著性检验。
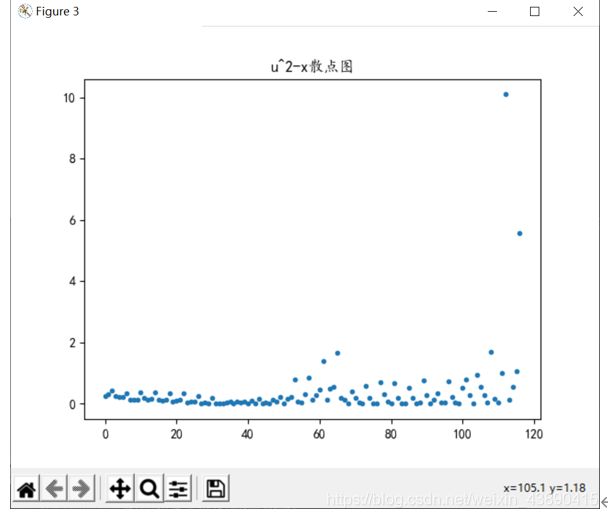
μ^2-x 图
可以从散点图看出,u^2的值在0~10之间,大致呈现为一条斜率为0的直线,不具有异方差性。
预测
经过检验后,通过多元回归模型进行预测,当 x1=8.09711 x2=1.20171 x3=1.00671时 求得预测值国民生产总值为22.568万亿元,实际值为24.93101万亿元,可见还是有一定的误差。
3.3实验总结
本次实验进行了多元线性回归的分析与预测检验,由于上次实验中已经进行了一元线性回归的编码,本次实验就想尝试一下多元线性回归。在本次实验中寻找数据变成了一大难题,由于需要解释变量与被解释变量具有一定的相关性,找了许多数据都不具有太好的效果,最后在国家统计局找到了国民生产总值的数据,进行绘图分析之后,发现国民生产总值与工业、建筑业、交通业增长值可能具有线性相关关系,便进行了回归分析。在得到回归方程后计算了标准估计误差,进行了拟合优度检验与回归系数检验,通过检验后进行预测。虽然解释变量与被解释变量已经呈现高度相关性,但预测出来的结果仍然存在一定的偏差,但总的来说还是有不错的效果。