算法学习 - 模拟滤波器（巴特沃斯、贝塞尔、切比雪夫、椭圆）及IIR滤波器设计

摘要：
在进行信号处理算法的嵌入式代码实现时，经常需要设计滤波器来对信号进行预处理或者后处理。常用的有IIR滤波器和FIR滤波器。虽然IIR滤波器在稳定性和相位响应上比FIR滤波器较差，但是在相同滤波需要下IIR的MIPS和内存要求要少很多。本文将从工程实践的角度来讲解IIR滤波器的设计。本文采用间接法设计数字滤波器：先设计模拟低通滤波器在通过双线性变换法得到数字低通、高通、带通、带阻滤波器。
先介绍几种模拟滤波器及其特性，方便根据实际需求来选择滤波器类型。
1. 巴特沃斯 Butterworth

也被称作最大平坦滤波器。巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有纹波。
一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数，振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高，在阻频带振幅衰减速度越快。
MATLAB Butterwirth滤波器设计函数:
[b,a] = butter(n,Wn,‘ftype’)
[z,p,k] = butter(n,Wn,‘ftype’)
[A,B,C,D] = butter(n,Wn,‘ftype’)
n-滤波器阶数
‘ftype’ Wn归一化频率[0,1]
‘high’ 高通截断频率Wn
‘low’ 低通截断频率Wn
‘stop’ 带阻频率Wn = [w1 w2]
‘bandpass’ 带通频率Wn = [w1 w2]
z是零点响应矢量，p是极值响应矢量，k是gain值。
b,a 为IIR直接型的分子分母参数:

A,B,C,D是状态空间形式，u为输入，x为状态空间，y为输出。

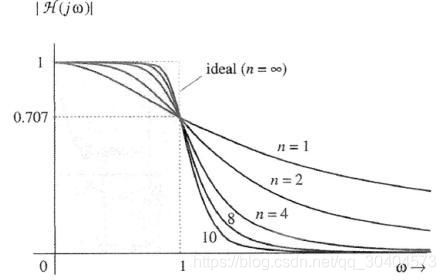
2. 贝塞尔 Bessel
具有最大平坦的群延迟（线性相位响应）的线性过滤器，常用在音频天桥系统中，可用于减少所有IIR滤波器固有的非线性相位失真。贝塞尔滤波器的阶跃响应很快，并且没有过冲或振铃，这使它在作为音频DAC输出端的平滑滤波器，或音频ADC输入端的抗混叠滤波器方面，是一种出色的选择。贝塞尔滤波器还可用于分析D类放大器的输出，以及消除其它应用中的开关噪声，来提高失真测量和示波器波形测量的精确度。为了达到特定的阻带衰减水平，需要设计更高阶的贝塞尔滤波器。
MATLAB Bessel低通滤波器设计函数:
[b,a] = besself(n,Wn)
[z,p,k] = butter(n,Wn)
[A,B,C,D] = butter(n,Wn)
由于besself只能设计模拟滤波器参数，所以需要用函数bilinear来转换成数字滤波器参数。
[zd,pd,kd] = bilinear(z,p,k,Fs);
[bd,ad] = bilinear(z,p,k,Fs);
[Ad,Bd,Cd,Dd] = bilinear(z,p,k,Fs);

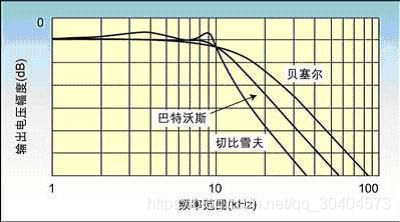
3. 切比雪夫 Chebyshev

是在通带或阻带上频率响应幅度等波纹波动的滤波器。切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。
I型切比雪夫滤波器在通带（或称“通频带”）上频率响应幅度等波纹波动;
MATLAB Cheby I 型滤波器设计函数:
[b,a] = cheby1(n,R,Wp,‘ftype’)
[z,p,k] = cheby1(n,R,Wp,‘ftype’)
[A,B,C,D] = cheby1(n,R,Wp,‘ftype’)
R - 波纹峰峰值（dB）
Wp - 归一化通带边缘频率
ftype - ‘high’ ‘low’ ‘stop’

II型切比雪夫滤波器在阻带（或称“阻频带”）上频率响应幅度等波纹波动的滤波器。
MATLAB Cheby II 型滤波器设计函数:
[b,a] = cheby2(n,R,Wst,‘ftype’)
[z,p,k] = cheby1(n,R,Wst,‘ftype’)
[A,B,C,D] = cheby1(n,R,Wst,‘ftype’)
Wst - 归一化阻带边缘频率
ftype - ‘high’ ‘low’ ‘stop’

4. 椭圆 Elliptic
椭圆滤波器是在通带和阻带等波纹的一种滤波器。
椭圆滤波器相比其他类型的滤波器，在阶数相同的条件下有着最小的通带和阻带波动。
从传递函数来看，巴特沃斯和切比雪夫滤波器的传输函数都是一个常数除以一个多项式, 为全极点网络, 仅在无限大阻带处衰减为无限大. 而椭圆函数滤波器在有限频率上既有零点又有极点。
极零点在通带内产生等波纹, 阻带内的有限传输零点减少了过渡区, 可获得极为陡峭的衰减曲线。也就是说在阶数相同的条件下,椭圆滤波器相比于其他类型的滤波器，能获得更窄的过渡带宽和较小的阻带波动, 就这点而言, 椭圆滤波器是最优的。它陡峭的过渡带特性是用通带和阻带的起伏为代价来换取的，并且在通带和阻带的波动相同，这一点区别于在通带和阻带都平坦的巴特沃斯滤波器，以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。
MATLAB Ellip 型滤波器设计函数:
[b,a] = ellip(n,Rp,Rs,Wp,‘ftype’)
[z,p,k] = ellip(n,Rp,Rs,Wp,‘ftype’)
[A,B,C,D] = ellip(n,Rp,Rs,Wp,‘ftype’)
Rp - 通带段波纹峰峰值（dB）
Rs - 阻带段波纹峰峰值（dB）
Wp - 归一化通带边缘频率
ftype - ‘high’ ‘low’ ‘stop’

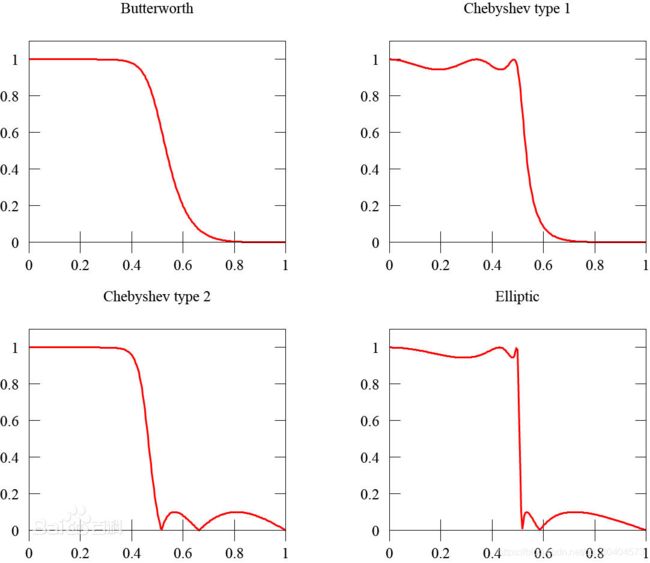
总结：
1.贝塞尔具有最线性的相位响应，但是衰减较慢。
2.巴特沃斯具有最平坦的通带。
3.椭圆滤波器衰减最快，但是通带、阻带都有波纹。
4.切比雪夫滤波器衰减比巴特沃斯快，但比椭圆滤波器慢，波纹区域可选择。