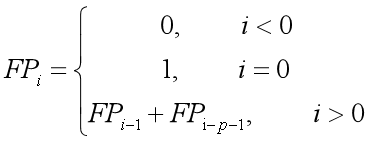位平面分解技术

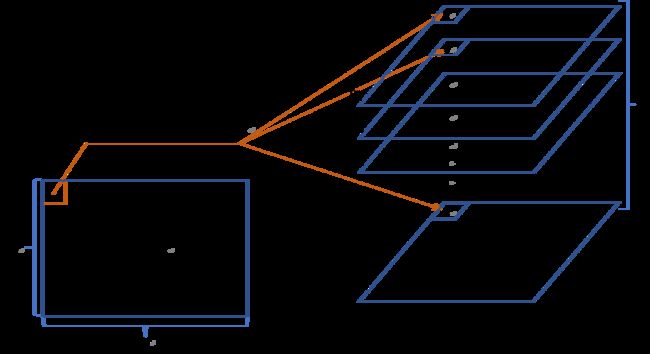
将灰度图中处于同一个比特位上的二进制像素值进行组合，得到一副二进制值图像，该图像称为灰度图的一个位平面。这个过程为平面分解。目前常见的平面分解技术有三种，分别是二进制位平面分解（BBD）、格雷码位平面分解技术（GCBD）以及截断斐波那契P码位平面分解技术（TFPBD）。BBD以及GCBD是两种传统的分解方法,他们可以将灰度图像分解成八个二进制平面。而TFPBD是一种参数位平面分解方法（可以将一张图像分解成N张子图，这里的N可以由参数调解）。

二进制位平面分解技术（BBD)

对于任何一个非负的整数都可以被一个二进制序列所表示，数学公式如下所示：

对于一般灰度图像而言，其灰度值通常是一个0到255之间的十进制数，那么每一个像素都可以由8位二进制序列唯一表示。因此，BBD可以将灰度图像拆分成8个二进制平面。第一个位平面是由灰度图像中每一个像素的二进制表示的所有第一位所组成的，如下图我们展示了将一个lena图分解成八张位平面子图的效果。

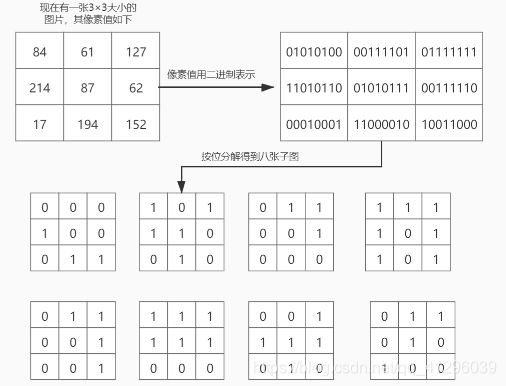
下图展示了将lena图分解后，各个平面图的样子，其中（a）为lena的原图，从(b)到（i)展示了从最低位平面到最高位平面，其中我们可以很明显发现第八张子图(i)最接近lena的原图，这也就说明了在组成一张图的过程中，高位的图往往起到了更加关键的作用。

python代码如下

import cv2
import numpy as np

image = cv2.imread("lena.bmp", 0)
h, w = image.shape

x = np.zeros((h, w, 8), dtype=np.uint8)
for i in range(8):
    x[:, :, i] = 2 ** i

r = np.zeros((h, w, 8), dtype=np.uint8)
for i in range(8):
    r[:, :, i] = cv2.bitwise_and(image, x[:, :, i])
    mask = r[:, :, i] > 0
    r[mask] = 255

    cv2.imshow(str(i), r[:, :, i])

cv2.waitKey()
cv2.destroyAllWindows()

matlab代码如下

clc;
clear all;
img = imread('lena.bmp');

% 获得比特平面分层后的图像
imageBit = myImageBitPlaneSlicing(img);
[r c k] = size(imageBit);
% 画出原图像
subplot(3,3,1);
imshow(img);
title('原始图像：EXP3C.tif','FontSize',20,'FontName','微软雅黑');
start = 2;
% 分别画出比特平面分层后的图像
for k = 1 : 8
    img_temp = imageBit(1:r,1:c,k);
    subplot(3,3,start);
    imshow(mat2gray(img_temp));
    pic_title = sprintf('第 %d 阶比特平面图像',k);
    title(pic_title,'FontSize',20,'FontName','微软雅黑');
    start = start + 1;
end

myImageBitPlaneSlicing(img)函数

function imageBit = myImageBitPlaneSlicing(img)
% 用于比特平面分层
% img：一幅m×n×1的8比特图像;
% imageBit：一个m×n×i (i = 1, 2, …, 8)的矩阵，第i个通道上存储第i阶比特平面图像

img_double = double(img);
[r c] = size(img_double);
imageBit = zeros(r,c,8);
% 遍历每一个像素点，将其值转换为8位2进制字符串，然后提取转型并赋值到对应比特平面
for row = 1 : r
    for col = 1 : c
        % 将灰度级转为8位2进制字符串
        bin_str = dec2bin(img_double(row, col),8);
        for i = 1 : 8
            % 提取对应位置的字符，转型后赋值到对应平面的对应位置
            digit = str2double(bin_str(i));
            imageBit(row,col,9-i) = digit;
        end
    end
end
imageBit = uint8(imageBit);

格雷码位平面分解技术（GCBD）

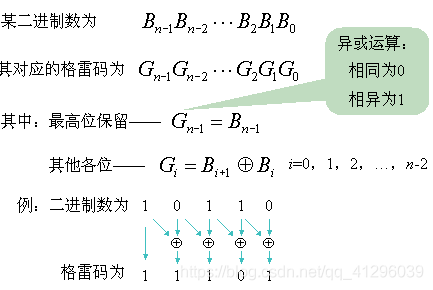
格雷码，又叫循环二进制码或反射二进制码，格雷码是我们在工程中常会遇到的一种编码方式，它的基本的特点就是任意两个相邻的代码只有一位二进制数不同,其数学表达式如下，其中b(i)和g(i)分别是非负十进制数N的二进制表示和格雷码表示。

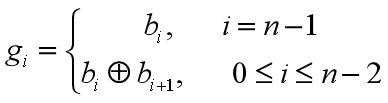
二进制码转换成二进制格雷码示例

格雷码位平面分解流程图

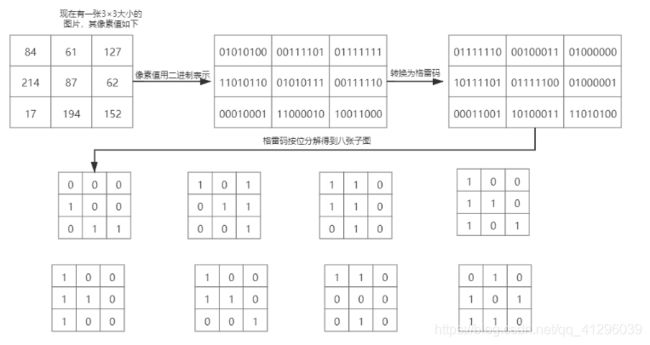
与BBD类似，灰度图像也可以分解成8个格雷码位平面。但是，对于一般的图像，GCBD的每一个位平面的内容与BBD种相对于的位平面的内容几乎是完全不同的。这种分解方法通常可以大大减小灰度变化所带来的影响。

P-Fibonacci位平面分解(TFPBs)

对于一个P-Fibonacci序列其标准数学定义如下：

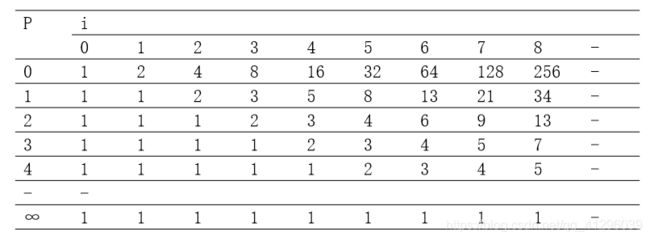
上述公式中 i 为序列的位置索引，非负整数是距离参数。P-Fibonacci数列数列会根据不同的P值而变化。如下表，我们给出了一些例子。同时我们注意到P-Fibonacci数列可以导出两个数列的幂(p=0)以及最传统的斐波那契数列(p=1)。

当P=1时，我们看到P-Fibonacci变成了我们最传统的Fibonacci数列。

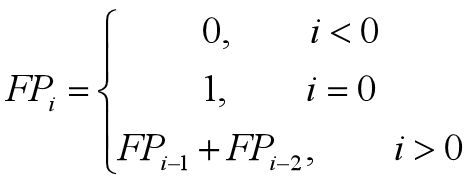
类似于BBD，图像也可以分解成截断的斐波那契p码位平面(TFPBs)。与BBD和GCBD不同，截断斐波那契p码位平面分解是一种参数相关的分解方法。对于特定的图像，TFPBD可以生成八个以上的位平面。例如，一个灰度图像可以分解成p=1的12个位平面。此外，随着p值的变化，位平面的数量和每个位平面中的内容是不同的。