数学建模方法 —【06】拟合方法之curve_fit
拟合方法——curve_fit
今天来说说curve_fit拟合方法,在前面的博文中,我也介绍了其他两种拟合方法以及拟合优度的计算,有兴趣的读者可以看看:
数学建模方法—【03】拟合优度的计算(python计算)
数学建模方法—【04】拟合方法之np.polyfit、np.poly1d
数学建模方法 — 【05】 拟合方法之leastsq
1. 概念:
curve_fit是使用非线性最小二乘法将函数f进行拟合,寻找到最优曲线.
来看看官网对这个方法的解释吧:
scipy.optimize.curve_fit(f,xdata,ydata,p0 = None,sigma = None,absolute_sigma = False,check_finite = True,bounds = -inf ,inf,method = None,jac = None,** kwargs)
介绍一下最常用也是最基本的参数:
# 参数
f: 模型函数f(x,…)。它必须将自变量作为第一个参数,其余你需要求的参数都放后面
xdata: 数组对象,测量数据的自变量。对于具有k个预测变量的函数,通常应为M长度序列或(k,M)形数组。
ydata: 数组对象,相关数据,长度M array-标称。f(xdata, ...)
# 返回值
popt: 数组,参数的最佳值,以使的平方残差之和最小。f(xdata, *popt) - ydata
pcov: 二维阵列,popt的估计协方差。对角线提供参数估计的方差。
2. 使用
curve_fit可以自定义拟合函数,所以可以拟合的函数很多。今天我举几个比较常见也常用的栗子吧。
<1> 多项式拟合
步骤1: 准备工作
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
# 忽略除以0的报错
np.seterr(divide='ignore', invalid='ignore')
# 拟合数据集
x = [4, 8, 10, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75, 78]
x_arr = np.array(x)
y_arr = np.array(y)
步骤2: 建立自定义方程函数
# 一阶函数方程(直线)
def func_1(x, a, b):
return a*x + b
# 二阶曲线方程
def func_2(x, a, b, c):
return a * np.power(x, 2) + b * x + c
# 三阶曲线方程
def func_3(x, a, b, c, d):
return a * np.power(x, 3) + b * np.power(x, 2) + c * x + d
# 四阶曲线方程
def func_4(x, a, b, c, d, e):
return a * np.power(x, 4) + b * np.power(x, 3) + c * np.power(x, 2) + d * x + e
步骤3: 获取拟合后的参数(各项的系数)
# 拟合参数都放在popt里,popt是个数组,参数顺序即你自定义函数中传入的参数的顺序
popt1, pcov1 = curve_fit(func_1, x_arr, y_arr)
a1 = popt1[0]
b1 = popt1[1]
popt2, pcov2 = curve_fit(func_2, x_arr, y_arr)
a2 = popt2[0]
b2 = popt2[1]
c2 = popt2[2]
popt3, pcov3 = curve_fit(func_3, x_arr, y_arr)
a3 = popt3[0]
b3 = popt3[1]
c3 = popt3[2]
d3 = popt3[3]
popt4, pcov4 = curve_fit(func_4, x_arr, y_arr)
a4 = popt4[0]
b4 = popt4[1]
c4 = popt4[2]
d4 = popt4[3]
e4 = popt4[4]
步骤4: 获取拟合得到的目标数据
yvals1 = func_1(x_arr, a1, b1)
print("一阶拟合数据为: ", yvals1)
yvals2 = func_2(x_arr, a2, b2, c2)
print("二阶拟合数据为: ", yvals2)
yvals3 = func_3(x_arr, a3, b3, c3, d3)
print("三阶拟合数据为: ", yvals3)
yvals4 = func_4(x_arr, a4, b4, c4, d4, e4)
print("四阶拟合数据为: ", yvals4)
输出结果为:
一阶拟合数据为: [31.77232593 33.77237512 34.77239971 35.77242431 42.27258418 45.77267026 51.27280553 58.77298999 61.27305148 64.27312526 69.27324824]
二阶拟合数据为: [39.51376772 37.97901745 37.36923348 36.86451029 36.14466602 37.59562119 42.47594786 54.25265173 59.49147942 66.64482407 80.66828072]
三阶拟合数据为: [34.98075096 37.25383345 38.11790383 38.82289993 40.6971475 40.84831314 42.03722659 50.07165835 55.48758658 64.39887551 86.28380105]
四阶拟合数据为: [19.44928601 40.05545824 46.36360873 50.48324909 44.88547212 34.26368355 27.43335049 49.97112988 62.51444438 75.84652416 77.73379333]
步骤5: 求拟合优度
这里求拟合优度的函数是我自己编写的,所以有需要的读者可以到我前面的文章看一下: 数学建模方法—【03】拟合优度的计算(python计算)
rr1 = goodness_of_fit(yvals1, y)
print("一阶曲线拟合优度为%.5f" % rr1)
rr2 = goodness_of_fit(yvals2, y)
print("二阶曲线拟合优度为%.5f" % rr2)
rr3 = goodness_of_fit(yvals3, y)
print("三阶曲线拟合优度为%.5f" % rr3)
rr4 = goodness_of_fit(yvals4, y)
print("四阶曲线拟合优度为%.5f" % rr4)
输出结果为:
一阶曲线拟合优度为0.52079
二阶曲线拟合优度为0.64095
三阶曲线拟合优度为0.67675
四阶曲线拟合优度为0.95310
步骤6: 绘图
figure3 = plt.figure(figsize=(8,6))
plt.plot(x_arr, yvals1, color="#72CD28", label='一阶拟合曲线')
plt.plot(x_arr, yvals2, color="#EBBD43", label='二阶拟合曲线')
plt.plot(x_arr, yvals3, color="#50BFFB", label='三阶拟合曲线')
plt.plot(x_arr, yvals4, color="gold", label='四阶拟合曲线')
plt.scatter(x_arr, y_arr, color='black', marker="X", label='原始数据')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定legend的位置右下角
plt.title('curve_fit 1~5阶拟合曲线')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.show()
<2> 幂函数拟合
步骤1: 准备工作
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
# 忽略除以0的报错
np.seterr(divide='ignore', invalid='ignore')
# 拟合数据集
x = [4, 8, 10, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75, 78]
x_arr = np.array(x)
y_arr = np.array(y)
步骤2: 建立自定义方程函数
# x
def pow_func(x, a, b):
return a * x + b
# x^2
def pow2_func(x, a, b):
return a * x**2 + b
# x^(-1)
def pow3_func(x, a, b):
return a / x + b
# x^(-2)
def pow4_func(x, a, b):
return a / x**2 + b
# 当然也可以直接把指数直接设置为参数,求解最优指数
# x^(c)
def pow5_func(x, a, b, c):
return a * x**b + c
步骤3: 获取拟合后的参数(各项的系数)
popt_pow, pcov_pow = curve_fit(pow_func, x_arr, y_arr)
a_pow = popt_pow[0]
b_pow = popt_pow[1]
popt_pow2, pcov_pow2 = curve_fit(pow2_func, x_arr, y_arr)
a_pow2 = popt_pow2[0]
b_pow2 = popt_pow2[1]
popt_pow3, pcov_pow3 = curve_fit(pow3_func, x_arr, y_arr)
a_pow3 = popt_pow3[0]
b_pow3 = popt_pow3[1]
popt_pow4, pcov_pow4 = curve_fit(pow4_func, x_arr, y_arr)
a_pow4 = popt_pow4[0]
b_pow4 = popt_pow4[1]
popt_pow5, pcov_pow5 = curve_fit(pow5_func, x_arr, y_arr)
a_pow5 = popt_pow5[0]
b_pow5 = popt_pow5[1]
c_pow5 = popt_pow5[2]
步骤4: 获取拟合得到的目标数据
yvals_pow = pow_func(x_arr, a_pow, b_pow)
print("x曲线拟合值为: ", yvals_pow)
yvals_pow2 = pow2_func(x_arr, a_pow2, b_pow2)
print("x^2曲线拟合值为: ", yvals_pow2)
yvals_pow3 = pow3_func(x_arr, a_pow3, b_pow3)
print("1/x曲线拟合值为: ", yvals_pow3)
yvals_pow4 = pow4_func(x_arr, a_pow4, b_pow4)
print("1/x^2曲线拟合值为: ", yvals_pow4)
yvals_pow5 = pow5_func(x_arr, a_pow5, b_pow5, c_pow5)
print("1/x^b曲线拟合值为: ", yvals_pow5)
输出结果为:
x曲线拟合值为: [31.77232593 33.77237512 34.77239971 35.77242431 42.27258418 45.77267026 51.27280553 58.77298999 61.27305148 64.27312526 69.27324824]
x^2曲线拟合值为: [34.80057891 35.11982255 35.35925527 35.65189527 38.85098253 41.50469524 46.99169521 57.06782243 61.0916224 66.35914237 76.20248777]
1/x曲线拟合值为: [19.42127949 38.7746244 42.64529339 45.22573938 51.93489894 53.28963309 54.52734701 55.45854243 55.67040171 55.88410324 56.16813692]
1/x^2曲线拟合值为: [17.68878189 44.33097332 47.52803629 49.26471247 52.30231699 52.65665814 52.90431237 53.04274816 53.0685023 53.0923241 53.12063398]
1/x^b曲线拟合值为: [37.37457119 37.38605022 37.40139652 37.42710579 38.11783665 39.17698704 42.5750987 52.5806134 57.82828391 65.71578329 83.41577262]
步骤5: 求拟合优度
这里求拟合优度的函数goodness_of_fit是我自己编写的,所以有需要的读者可以到我前面的文章看一下: 数学建模方法—【03】拟合优度的计算(python计算)
rr_pow = goodness_of_fit(yvals_pow, y)
print("x曲线拟合优度为%.5f" % rr_pow)
rr_pow2 = goodness_of_fit(yvals_pow2, y)
print("x^2曲线拟合优度为%.5f" % rr_pow2)
rr_pow3 = goodness_of_fit(yvals_pow3, y)
print("1/x曲线拟合优度为%.5f" % rr_pow3)
rr_pow4 = goodness_of_fit(yvals_pow4, y)
print("1/x^2曲线拟合优度为%.5f" % rr_pow4)
rr_pow5 = goodness_of_fit(yvals_pow5, y)
print("1/x^b曲线拟合优度为%.5f" % rr_pow5)
输出结果为:
x曲线拟合优度为0.52079
x^2曲线拟合优度为0.61012
1/x曲线拟合优度为0.35716
1/x^2曲线拟合优度为0.31037
1/x^b曲线拟合优度为0.65942
步骤6: 绘图
figure4 = plt.figure(figsize=(8,6))
plt.plot(x_arr, yvals_pow, color="#cea2fd", label='x曲线拟合曲线')
plt.plot(x_arr, yvals_pow2, color="#0bf9ea", label='x^2曲线拟合曲线')
plt.plot(x_arr, yvals_pow3, color="#25ff29", label='1/x曲线拟合曲线')
plt.plot(x_arr, yvals_pow4, color="gold", label='1/x^2拟合曲线')
plt.plot(x_arr, yvals_pow5, color="#13EAC9", label='1/x^b拟合曲线')
plt.scatter(x_arr, y_arr, color='black', marker="*", label='原始数据')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定legend的位置右下角
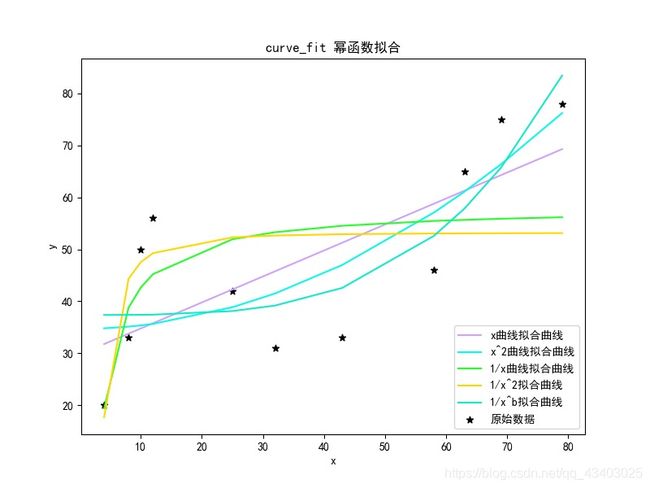
plt.title('curve_fit 幂函数拟合')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.show()
<3> 指数函数拟合
由于篇幅关系,我就直接把整体代码放上来了:
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize
# 忽略除以0的报错
np.seterr(divide='ignore', invalid='ignore')
# 拟合数据集
x = [4, 8, 10, 12, 25, 32, 43, 58, 63, 69, 79]
y = [20, 33, 50, 56, 42, 31, 33, 46, 65, 75, 78]
x_arr = np.array(x)
y_arr = np.array(y)
def exp_func(x, a, b, c):
return a * np.exp(b / x) + c
def exp2_func(x, a, b, c, d):
return a * np.power(b, c * x) + d
popt_exp, pcov_exp = curve_fit(exp_func, x_arr, y_arr)
a_exp = popt_exp[0]
b_exp = popt_exp[1]
c_exp = popt_exp[2]
popt_exp2, pcov_exp2 = curve_fit(exp2_func, x_arr, y_arr)
a_exp2 = popt_exp2[0]
b_exp2 = popt_exp2[1]
c_exp2 = popt_exp2[2]
d_exp2 = popt_exp2[3]
yvals_exp = exp_func(x_arr, a_exp, b_exp, c_exp)
print("e^x曲线拟合值为: ", yvals_exp)
yvals_exp2 = exp2_func(x_arr, a_exp2, b_exp2, c_exp2, d_exp2)
print("b^x曲线拟合值为: ", yvals_exp2)
rr_exp = goodness_of_fit(yvals_exp, y)
print("e^x曲线拟合优度为%.5f" % rr_exp)
rr_exp2 = goodness_of_fit(yvals_exp2, y)
print("b^x曲线拟合优度为%.5f" % rr_exp2)
figure5 = plt.figure(figsize=(8,6))
plt.plot(x_arr, yvals_exp, color="#cea2fd", label='e^x曲线拟合曲线')
plt.plot(x_arr, yvals_exp, color="#ffdf22", label='b^x曲线拟合曲线')
plt.scatter(x_arr, y_arr, color='#019529', marker="d", label='原始数据')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定legend的位置右下角
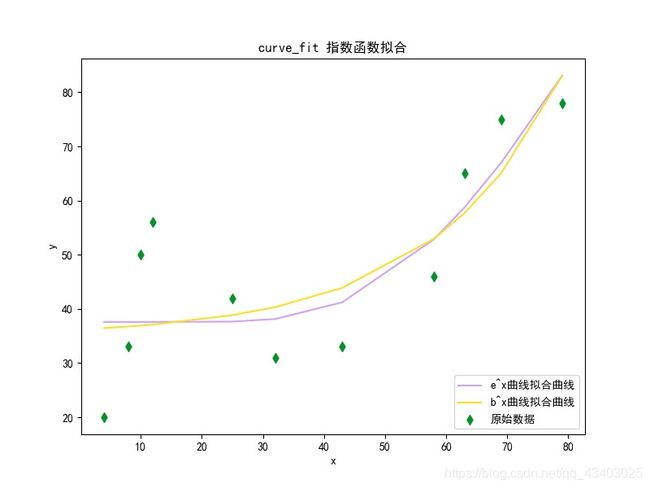
plt.title('curve_fit 指数函数拟合')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.show()
输出结果为:
e^x曲线拟合值为: [37.5923875 37.5923875 37.59238754 37.59238969 37.65956686 38.13325449 41.22901253 52.84521457 58.72785567 66.9624748 83.07305172]
b^x曲线拟合值为: [36.46910069 36.76144961 36.92956697 37.11424962 38.84790086 40.32499745 43.89141523 52.9351502 57.67036988 65.03579202 83.01834076]
e^x曲线拟合优度为0.67952
b^x曲线拟合优度为0.64644
<4> 指数的指数函数拟合
def special_func(x, a, b, c):
return a * np.exp(np.exp(b / x)) + c
popt_spec, pcov_spec = curve_fit(special_func, x_arr, y_arr)
a_spec = popt_spec[0]
b_spec = popt_spec[1]
c_spec = popt_spec[2]
yvals_spec = special_func(x_arr, a_spec, b_spec, c_spec)
print("曲线拟合值为: ", yvals_spec)
rr_spec = goodness_of_fit(yvals_spec, y)
print("指数的指数函数曲线拟合优度为%.5f" % rr_spec)
figure6 = plt.figure(figsize=(8,6))
plt.plot(x_arr, yvals_spec, color="#cea2fd", label='指数的指数曲线拟合曲线')
# plt.plot(x_arr, yvals_spec, color="#ffdf22", label='b^x曲线拟合曲线')
plt.scatter(x_arr, y_arr, color='#019529', marker="8", label='原始数据')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定legend的位置右下角
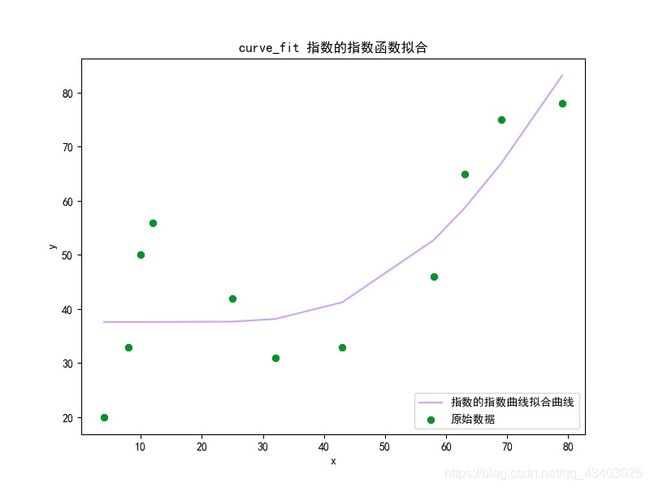
plt.title('curve_fit 指数的指数函数拟合')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.show()
输出的结果为:
曲线拟合值为: [37.6112808 37.6112808 37.61128085 37.6112833 37.68093904 38.16157746 41.25325308 52.78393414 58.64103037 66.87908303 83.1550442 ]
指数的指数函数曲线拟合优度为0.67875
<5> 高斯函数拟合
# 先创造数据
x_gauss = np.arange(40)
y_gauss = list(range(20)) + list(reversed(list(range(20)))) + .6 * np.random.normal(size=len(x_gauss))
# 再拟合
# 高斯函数
def gauss_func(x, a, b, c, sigma):
return a * np.exp(-(x - b) ** 2 / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi)) + c
popt_gauss, pcov_gauss = curve_fit(gauss_func, x_gauss, y_gauss)
a_gauss = popt_gauss[0]
b_gauss = popt_gauss[1]
c_gauss = popt_gauss[2]
sigma = popt_gauss[3]
yvals_gauss = gauss_func(x_gauss, a_gauss, b_gauss, c_gauss, sigma)
rr_gauss = goodness_of_fit(yvals_gauss, y_gauss)
print("高斯函数曲线拟合优度为%.5f" % rr_gauss)
figure7 = plt.figure(figsize=(8,6))
plt.plot(x_gauss, yvals_gauss, color="#cea2fd", label='高斯函数拟合曲线')
plt.scatter(x_gauss, y_gauss, color='#13bbaf', marker=">", label='原始数据')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=4) # 指定legend的位置右下角
plt.title('curve_fit 高斯函数拟合')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.show()
输出结果为:
高斯函数曲线拟合值为: [ 0.42825029 1.07423629 1.80592935 2.62424791 3.52756905 4.51134387
5.56779827 6.68575134 7.85058114 9.04436102 10.24618097 11.43265716
12.57861996 13.65795724 14.6445766 15.51343891 16.24160709 16.8092491
17.20053444 17.40436732 17.41490944 17.23185776 16.86045902 16.31125985
15.59960926 14.74494611 13.7699178 12.69938584 11.55937915 10.37605595
9.17473136 7.97901918 6.81012573 5.68632016 4.6225927 3.6304987
2.71817544 1.890509 1.14942233 0.4942522 ]
高斯函数曲线拟合优度为0.97923