python：curve_fit()实现任意形式的曲线拟合

本函数不仅可以用于直线、二次曲线、三次曲线的拟合和绘制，仿照代码中的形式，可以适用于任意形式的曲线的拟合和绘制，只要定义好合适的曲线方程即可。

特点⬇ xdata可以是数组，就是可以实现多元回归

xdata：array_like or object

The independent variable where the data is measured. Should usually be an M-length sequence or an (k,M)-shaped array for functions with k predictors, but can actually be any object.

应用例子：

下面是从1月开始阿拉斯加每个月的温度极值（摄氏度）：
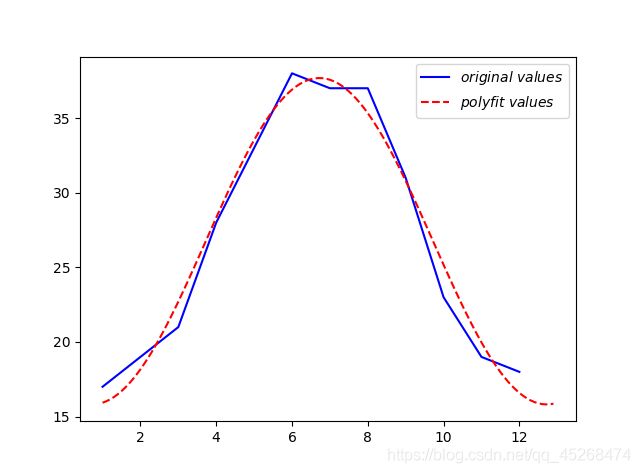
最大值：17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18
最小值：-62, -59, -56, -46, -32, -18, -9, -13, -25, -46, -52, -58
用scipy.optimize.curve_fit()拟合这个函数与数据

分析：

可以看出温度是以周期为12的正弦函数（这里一开始被我当成365了结果咋也做不好。。。)

构建函数
$$f(x)=a\cdot sin(\frac{2\pi \cdot x}{12}+b)+c$$

代码如下（模板，fund里代什么函数都可以，然后改xdata和ydata（这俩是拟合对象，模板里是先生成完全对应的y再加上随机数把它搞乱），有几个参数就对应倒第四行y2里的popt参数个数）：

from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np

def fund(x,a,b,c):
    return a*np.sin(2*np.pi/12*x+b)+c

x=np.arange(1, 13)
x2=np.arange(1,13,0.1)
y=[17,19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18]
fig,ax=plt.subplots()
popt, pcov=curve_fit(fund, x, y)
#popt数组中，三个值分别是待求参数a,b,c
ax.plot(x,y,'b-')
ax.legend(r'$original\ values$')
y2 = [fund(xx,popt[0],popt[1],popt[2]) for xx in x2]
ax.plot(x2,y2,'r--')
ax.legend(r'$polyfit\ values$')
print (popt)
plt.show()

使用本函数完成拟合，下面是原始数据和拟合曲线）：


实现方法见官方文档 curve_fit文档