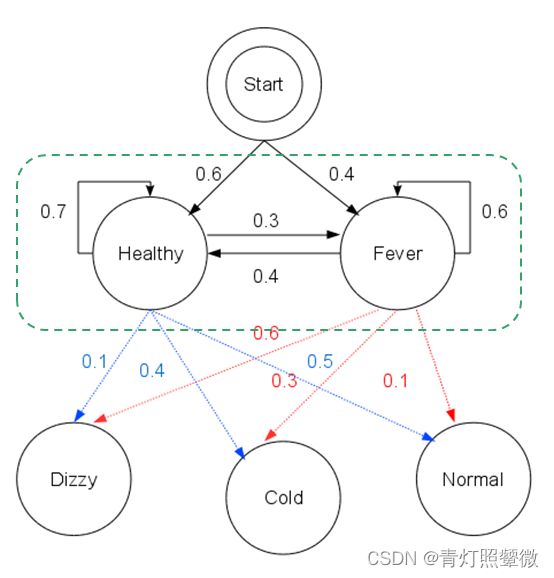
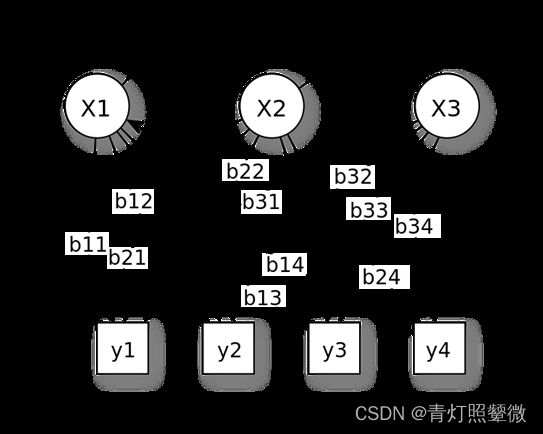
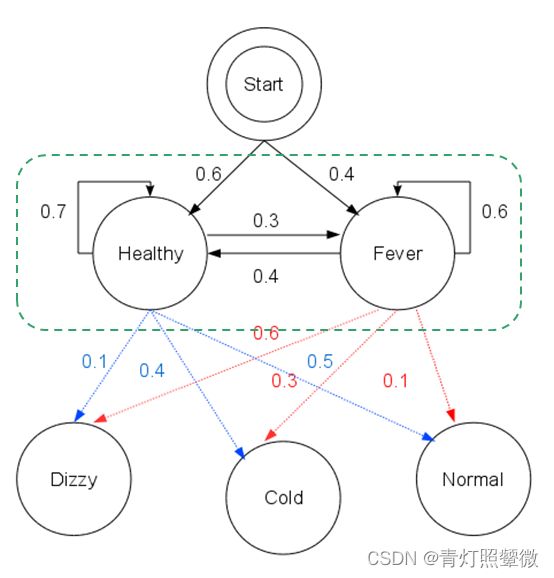
- Python爬虫【四十五章】爬虫攻防战:异步并发+AI反爬识别的技术解密
程序员_CLUB
Python入门到进阶python爬虫人工智能
目录引言:当爬虫工程师遇上AI反爬官一、异步并发基础设施层1.1混合调度框架设计1.2智能连接池管理二、机器学习反爬识别层2.1特征工程体系2.2轻量级在线推理三、智能决策系统3.1动态策略引擎3.2实时对抗案例四、性能优化实战4.1全链路压测数据4.2典型故障处理案例五、总结:构建智能化的爬虫生态系统Python爬虫相关文章(推荐)引言:当爬虫工程师遇上AI反爬官在大数据采集领域,我们正经历着技
- 走进区块城市,开启你的元宇宙之旅!
口碑信息传播者
随着科技的飞速发展,虚拟现实、区块链、人工智能等前沿技术逐渐融入我们的生活。在这个大背景下,元宇宙概念应运而生,成为全球关注的焦点。本文将带领读者走进区块城市,一探元宇宙的究竟,感受这个未来世界的魅力。探索未来,触碰无限可能!国内区块链元宇宙正引领一场前所未有的科技革命,现在正是您加入这场盛宴的最佳时机!在这里,您将亲身体验到一个全新的虚拟世界,感受与现实世界无缝对接的震撼体验。加入国内区块链元宇
- AI人工智能领域知识图谱在文本分类中的应用技巧
AI天才研究院
AI大模型企业级应用开发实战人工智能知识图谱分类ai
AI人工智能领域知识图谱在文本分类中的应用技巧关键词:知识图谱、文本分类、图神经网络、实体关系抽取、深度学习、自然语言处理、特征融合摘要:本文深入探讨了知识图谱在文本分类任务中的应用技巧。我们将从知识图谱的基本概念出发,详细分析如何将结构化知识融入传统文本分类流程,介绍最新的图神经网络方法,并通过实际案例展示知识增强型文本分类系统的构建过程。文章特别关注知识表示学习与文本特征的融合策略,以及在不同
- 大学专业科普 | 人工智能、物联网和云计算技术
鸭鸭鸭进京赶烤
人工智能物联网云计算5G信号处理信息与通信网络
一、专业概述人工智能专业是一门融合计算机科学、数学、信息学等多学科知识的交叉学科。它旨在培养学生掌握人工智能领域的基本理论、方法和技能,以应对人工智能在各个领域的应用需求和发展挑战。二、主要课程基础课程:包括高等数学、线性代数、概率论与数理统计、离散数学等数学基础课程,为人工智能算法提供理论支撑;以及数据结构、算法设计与分析、计算机组成原理、操作系统、计算机网络等计算机科学基础课程,帮助学生理解人
- 解读一个大学专业——信号与图像处理
专业定义与核心内容维度内容定义研究如何采集、处理、分析和理解一维信号(语音、雷达、脑电)和二维/三维图像(医学、遥感、工业视觉)。关键词数字信号处理(DSP)、图像处理、计算机视觉、模式识别、压缩感知、深度学习、GPU加速、嵌入式系统。技术栈MATLAB/Python+OpenCV/PyTorch+DSP/FPGA+GPU(CUDA)第五届先进算法与信号、图像处理国际学术会议(AASIP2025)
- Pad Token技术原理与实现指南
Takoony
AI
目录概述理论基础:第一性原理分析技术实现机制工程最佳实践性能优化策略常见问题与解决方案技术发展趋势附录1.概述1.1文档目的本文档旨在深入阐述深度学习中PadToken的技术原理、实现机制及工程应用,为算法工程师提供全面的理论指导和实践参考。1.2适用范围自然语言处理模型开发序列数据批处理优化深度学习系统架构设计高性能计算资源管理1.3核心问题研究问题:为什么深度学习模型需要将变长序列统一到固定长
- 深度学习分布式训练:并行策略与通信机制的系统性分析
Takoony
深度学习分布式人工智能
1.引言随着深度学习模型规模的指数级增长,单一计算设备已无法满足训练需求。以GPT-3为例,其1750亿参数在FP16精度下需要约350GB存储空间(每个参数2字节),远超当前主流GPU的显存容量(如NVIDIAA100的80GB)。根据OpenAI的技术报告[1],即使使用最先进的硬件,单卡训练GPT-3需要355年。这一计算瓶颈催生了分布式训练技术的快速发展。本文将从理论基础出发,系统性地分析
- 转行网络安全需要学什么?(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全苏柒
web安全计算机网络网络安全运维转业程序员编程
什么是网络安全?网络安全是指保护网络系统的硬件、软件及其系统中的数据,破坏、更改、泄露,使系统连续可靠正常地运行,网络服务不会中断。未来,我国将着重发展数字经济,发展云计算、大数据、物联网、工业互联网、区块链和人工智能等产业,这些产业全部都基于网络互联。网络的安全就是以上这些产业能够良性发展的基础,也是建设制造强国和网络强国的基础保障。什么是网络安全工程师?网络安全工程师是负责保护计算机网络系统,
- 万字长文,解读大模型技术原理(非常详细)零基础入门到精通,收藏这一篇就够了
大模型是指具有大规模参数和复杂计算结构的机器学习模型。本文从大模型的发展历程出发,对大模型领域的各个技术细节进行详细解读,供大家在了解大模型基本知识的过程中起到一定参考作用。一、大模型的定义大语言模型作为一个被验证可行的方向,其“大”体现在训练数据集广,模型参数和层数大,计算量大,其价值体现在通用性上,并且有更好的泛化能力。这些模型通常由深度神经网络构建而成,拥有数十亿甚至数千亿个参数。大模型的设
- 转行网络安全需要学什么?(非常详细)从零基础到精通,收藏这篇就够了!
~小羊没烦恼~
黑客技术黑客网络安全web安全安全学习运维网络
什么是网络安全?网络安全是指保护网络系统的硬件、软件及其系统中的数据,破坏、更改、泄露,使系统连续可靠正常地运行,网络服务不会中断。未来,我国将着重发展数字经济,发展云计算、大数据、物联网、工业互联网、区块链和人工智能等产业,这些产业全部都基于网络互联。网络的安全就是以上这些产业能够良性发展的基础,也是建设制造强国和网络强国的基础保障。什么是网络安全工程师?网络安全工程师是负责保护计算机网络系统,
- 转行网络安全需要学什么?(非常详细)零基础入门到精通,收藏这一篇就够了
网络安全k叔
web安全计算机网络网络安全编程计算机转业信息安全
什么是网络安全?网络安全是指保护网络系统的硬件、软件及其系统中的数据,破坏、更改、泄露,使系统连续可靠正常地运行,网络服务不会中断。未来,我国将着重发展数字经济,发展云计算、大数据、物联网、工业互联网、区块链和人工智能等产业,这些产业全部都基于网络互联。网络的安全就是以上这些产业能够良性发展的基础,也是建设制造强国和网络强国的基础保障。什么是网络安全工程师?网络安全工程师是负责保护计算机网络系统,
- TensorFlow为AI人工智能航空航天领域带来变革
AI原生应用开发
人工智能tensorflowpythonai
TensorFlow为AI人工智能航空航天领域带来变革关键词:TensorFlow、人工智能、航空航天、机器学习、深度学习、神经网络、自主系统摘要:本文探讨了TensorFlow这一强大的机器学习框架如何推动航空航天领域的创新。我们将从基础概念入手,逐步深入分析TensorFlow在航天器导航、卫星图像处理、飞行器自主决策等关键应用场景中的实现原理。通过实际代码示例和架构图解,展示TensorFl
- 多语言文本分类在AI应用中的实践
AI原生应用开发
人工智能分类数据挖掘ai
多语言文本分类在AI应用中的实践关键词:多语言文本分类、自然语言处理、机器学习、深度学习、BERT、迁移学习、跨语言模型摘要:本文深入探讨多语言文本分类在AI领域的应用实践。我们将从基础概念出发,逐步讲解其核心原理、技术架构和实现方法,并通过实际案例展示如何构建一个高效的多语言文本分类系统。文章将涵盖从传统机器学习方法到最先进的深度学习技术,特别关注跨语言迁移学习在实际业务场景中的应用。背景介绍目
- 从零开始构建AI原生应用的认知架构
AI原生应用开发
AI-native架构ai
从零开始构建AI原生应用的认知架构关键词:AI原生应用、认知架构、机器学习、知识图谱、神经网络、智能决策、系统设计摘要:本文深入探讨如何从零开始构建AI原生应用的认知架构。我们将从基本概念出发,逐步解析认知架构的核心组件,包括知识表示、推理机制和学习能力等。通过生动的比喻和实际代码示例,帮助读者理解如何设计一个能够模拟人类认知过程的AI系统。文章还将介绍当前最先进的认知架构模型,并展望未来发展趋势
- Orange3实战教程:图像分析---图像嵌入
err2008
Orange3实战教程数据挖掘神经网络自然语言处理机器学习计算机视觉深度学习orange3中文版
图像嵌入通过深度神经网络实现图像嵌入。输入图像:图像列表。输出嵌入向量:用数字向量表示的图像。跳过的图像:未计算嵌入向量的图像列表。图像嵌入功能读取图像并将其上传至远程服务器或本地计算。深度学习模型用于为每张图像计算特征向量。该功能返回一个增强的数据表,包含额外的列(图像描述符)。图像可以通过导入图像小部件导入,也可以通过电子表格中的图像路径导入。在这种情况下,包含图像路径的列需要一个三行表头,第
- 宗毅说 | 乌卡瑟时代的生存思考
裂变学院
今天,互联网经济、人工智能、全球化发展对我们的影响,要比我们想象得大得多。在多股合力的相互作用下,这个时代的社会特征、商业特征与之前相比显著不同,我称之为乌卡瑟“VUCASE”。备注:乌卡瑟(VUCASE)这个术语是我自创的,来自于乌卡(VUKA)。VUCA是Volatility(易变性),Uncertainty(不确定性),Complexity(复杂性)、Ambiguity(模糊性)这四个英文单
- [论文阅读] 人工智能 + 软件工程 | 单会话方法论:一种以人类为中心的人工智能辅助软件开发协议
张较瘦_
前沿技术论文阅读人工智能软件工程
单一对话法(SCM):AI辅助软件开发的“全局对话”新思路SingleConversationMethodology:AHuman-CenteredProtocolforAI-AssistedSoftwareDevelopmentarXiv:2507.12665SingleConversationMethodology:AHuman-CenteredProtocolforAI-AssistedSo
- 如何安全使用人工智能大模型
人工智能大模型的安全漏洞在推送,你只要有不一样的解决方案他就会通过学习学会,在别人讨论相同问题时,就会作为解决问题的推荐方案。这种机制是没办法防的。鉴于此我们只能采取如下措施:1.绝对本地部署,就是部署好以后断网,因为你使用时他还是会手机数据往后台传送,我本地部署的大模型在推理时看性能,网络也是有数据流的。也不知道在交换什么。2.既然搞不清楚那就彻底不相信,断网。那么我们要加快进度,快速完成任务,
- PyTorch生成式人工智能(18)——循环神经网络详解与实现
盼小辉丶
pytorchrnn自然语言处理
PyTorch生成式人工智能(18)——循环神经网络详解与实现0.前言1.文本生成的挑战2.循环神经网络2.1文本数据2.2循环神经网络原理3.长短期记忆网络3.自然语言处理基础3.1分词3.2词嵌入3.3词嵌入在自然语言处理中的应用小结系列链接0.前言我们已经学习了如何生成数字和图像等内容。从本节开始,我们将主要聚焦于文本生成。人类语言极其复杂且充满细微差别,不仅仅涉及语法和词汇的理解,还包括上
- 【人工智能99问】卷积神经网络(CNN)的结构和原理是什么?(10/99)
文章目录卷积神经网络(CNN)的结构及原理一、CNN的核心结构1.输入层(InputLayer)2.卷积层(ConvolutionalLayer)2.卷积层的核心机制:局部感受野与权值共享3.池化层(PoolingLayer)4.全连接层(FullyConnectedLayer)5.输出层(OutputLayer)6.辅助层二、CNN的工作原理三、CNN的使用场景1.计算机视觉(最核心场景)2.其
- Deep Multi-scale Convolutional Neural Network for Dynamic Scene Deblurring 论文阅读
钟屿
论文阅读计算机视觉人工智能
用于动态场景去模糊的深度多尺度卷积神经网络摘要针对一般动态场景的非均匀盲去模糊是一个具有挑战性的计算机视觉问题,因为模糊不仅来源于多个物体运动,还来源于相机抖动和场景深度变化。为了去除这些复杂的运动模糊,传统的基于能量优化的方法依赖于简单的假设,例如模糊核是部分均匀或局部线性的。此外,最近的基于机器学习的方法也依赖于在这些假设下生成的合成模糊数据集。这使得传统的去模糊方法在模糊核难以近似或参数化的
- 基于Paillier同态加密算法的金融数据安全共享机制研究【附数据】
金融数据分析与建模专家金融科研助手|论文指导|模型构建✨专业领域:金融数据处理与分析量化交易策略研究金融风险建模投资组合优化金融预测模型开发深度学习在金融中的应用擅长工具:Python/R/MATLAB量化分析机器学习模型构建金融时间序列分析蒙特卡洛模拟风险度量模型金融论文指导内容:金融数据挖掘与处理量化策略开发与回测投资组合构建与优化金融风险评估模型期刊论文✅具体问题可以私信或查看文章底部二维码
- 吴恩达 机器学习cs229-学习笔记-更新中
是娜个二叉树!
机器学习学习笔记
吴恩达机器学习cs22901基础概念语言:Matlab/python监督学习定义:获取一组数据集拟合数据从X到Y的映射回归问题:预测的Y是连续的,Y是实数分类问题:分类指的是Y取离散值,输出是离散的两组,正示例和负示例,把所有样本推到这条直线上,用0,1,标识逻辑回归算法,拟合直线区分正,负示例处理相对大量特征的回归算法或者分类算法支持向量机算法:它使用的不是1,2,3,10个输入特征,而是使用无
- YOLOv8实现手写数字识别系统:从MNIST到实时摄像头检测
在深度学习领域,手写数字识别是一个经典问题,也是入门计算机视觉的重要案例。本文将介绍一个基于YOLOv8和MNIST数据集的手写数字识别系统,该系统不仅能识别静态图像中的数字,还能通过摄像头实时检测手写数字。个人博客:YOLOv8实现手写数字识别系统:从MNIST到实时摄像头检测-iDing's博客项目概述这个项目结合了传统的MNIST数据集和现代的目标检测算法YOLOv8,实现了以下功能:将MN
- 「日拱一码」033 机器学习——严格划分
胖达不服输
「日拱一码」机器学习人工智能严格划分组划分
目录简单随机划分(train_test_split)分组划分(GroupSplitting)简单分组划分(GroupSplitting)分层分组划分(StratifiedGroupSplitting)交叉验证法(Cross-Validation)分组K折交叉验证(GroupKFold)留一组法(LeaveOneGroupOut)简单随机划分(train_test_split)简单随机分组通过随机分
- 基于深度学习的手写数字和符号识别系统:YOLOv5/v6/v7/v8/v10模型实现与UI界面集成
YOLO实战营
深度学习YOLOui人工智能目标检测计算机视觉
1.引言随着人工智能和深度学习技术的发展,手写数字和符号识别已经成为计算机视觉领域的重要研究方向。手写识别在很多实际应用中扮演着关键角色,例如邮政编码识别、表单自动处理和智能教育系统等。传统的手写识别方法通常依赖于复杂的特征工程,而深度学习则能够自动从数据中学习到特征,极大地提高了识别精度和速度。本文将介绍如何构建一个基于YOLO系列模型(YOLOv5、YOLOv6、YOLOv7、YOLOv8、Y
- 【人工智能艺术革命:科技灵感与艺术创新的交融纪元】
陈辰学长
人工智能科技
【人工智能艺术革命:科技灵感与艺术创新的交融纪元】在21世纪的科技浪潮中,人工智能(AI)作为一股不可忽视的力量,正以前所未有的速度渗透并重塑着我们的生活、工作乃至艺术创作领域。其中,AI绘画作为科技与艺术深度融合的产物,不仅挑战了传统艺术的边界,更开启了一个充满无限想象与可能的新时代。本文将从AI绘画的定义与发展历程、技术原理、对艺术创作的影响、面临的挑战与机遇以及未来展望等多个维度,深入探讨这
- 从零开始:搭建你的人工智能开发环境
人工智能教程
人工智能YOLO机器学习transformer线性回归动态规划排序算法
前言在人工智能和机器学习的旅程中,一个稳定且高效的开发环境是成功的关键第一步。无论是初学者还是经验丰富的开发者,一个配置良好的开发环境都能大大提高工作效率,减少遇到的问题。本文将从零开始,逐步指导你如何搭建一个完整的人工智能开发环境,包括操作系统选择、Python安装、常用库的配置以及开发工具的选择。一、选择合适的操作系统(一)主流操作系统介绍在搭建人工智能开发环境时,首先需要选择一个合适的操作系
- 骗局揭露:光远投研会马光远,环境排放3.0被骗不靠谱!不可信!真相震惊!
易星辰分享普法
关于曝光网上光远投研会马光远在炒股群推荐智慧农业中粮仓平台骗局的文章,其内容主要揭示了近期频发的一种投资诈骗手段。以下是该骗局的主要特点和步骤:为什么明明跟老师对过视频,确认是本人,怎么还会被骗了?你有没有想过一个名人大咖怎么会有时间给你们一对一视频,其次我来给大家揭露一下,这个套路AI换脸骗局是一种利用人工智能技术,通过替换视频中的人脸来伪造身份或进行诈骗的行为。你的账户“余额”是真的吗?为什么
- 【Grafana】Prometheus指标可视化Grafana,手把手教你如何自定义图形
景天科技苑
grafanaprometheusprometheus可视化grafana自定义图形手撕grafana自定义监控图形
✨✨欢迎大家来到景天科技苑✨✨养成好习惯,先赞后看哦~作者简介:景天科技苑《头衔》:大厂架构师,华为云开发者社区专家博主,阿里云开发者社区专家博主,CSDN全栈领域优质创作者,掘金优秀博主,51CTO博客专家等。《博客》:Python全栈,前后端开发,小程序开发,人工智能,js逆向,App逆向,网络系统安全,数据分析,Django,fastapi,flask等框架,云原生k8s,Prometheu
- 书其实只有三类
西蜀石兰
类
一个人一辈子其实只读三种书,知识类、技能类、修心类。
知识类的书可以让我们活得更明白。类似十万个为什么这种书籍,我一直不太乐意去读,因为单纯的知识是没法做事的,就像知道地球转速是多少一样(我肯定不知道),这种所谓的知识,除非用到,普通人掌握了完全是一种负担,维基百科能找到的东西,为什么去记忆?
知识类的书,每个方面都涉及些,让自己显得不那么没文化,仅此而已。社会认为的学识渊博,肯定不是站在
- 《TCP/IP 详解,卷1:协议》学习笔记、吐槽及其他
bylijinnan
tcp
《TCP/IP 详解,卷1:协议》是经典,但不适合初学者。它更像是一本字典,适合学过网络的人温习和查阅一些记不清的概念。
这本书,我看的版本是机械工业出版社、范建华等译的。这本书在我看来,翻译得一般,甚至有明显的错误。如果英文熟练,看原版更好:
http://pcvr.nl/tcpip/
下面是我的一些笔记,包括我看书时有疑问的地方,也有对该书的吐槽,有不对的地方请指正:
1.
- Linux—— 静态IP跟动态IP设置
eksliang
linuxIP
一.在终端输入
vi /etc/sysconfig/network-scripts/ifcfg-eth0
静态ip模板如下:
DEVICE="eth0" #网卡名称
BOOTPROTO="static" #静态IP(必须)
HWADDR="00:0C:29:B5:65:CA" #网卡mac地址
IPV6INIT=&q
- Informatica update strategy transformation
18289753290
更新策略组件: 标记你的数据进入target里面做什么操作,一般会和lookup配合使用,有时候用0,1,1代表 forward rejected rows被选中,rejected row是输出在错误文件里,不想看到reject输出,将错误输出到文件,因为有时候数据库原因导致某些column不能update,reject就会output到错误文件里面供查看,在workflow的
- 使用Scrapy时出现虽然队列里有很多Request但是却不下载,造成假死状态
酷的飞上天空
request
现象就是:
程序运行一段时间,可能是几十分钟或者几个小时,然后后台日志里面就不出现下载页面的信息,一直显示上一分钟抓取了0个网页的信息。
刚开始已经猜到是某些下载线程没有正常执行回调方法引起程序一直以为线程还未下载完成,但是水平有限研究源码未果。
经过不停的google终于发现一个有价值的信息,是给twisted提出的一个bugfix
连接地址如下http://twistedmatrix.
- 利用预测分析技术来进行辅助医疗
蓝儿唯美
医疗
2014年,克利夫兰诊所(Cleveland Clinic)想要更有效地控制其手术中心做膝关节置换手术的费用。整个系统每年大约进行2600例此类手术,所以,即使降低很少一部分成本,都可以为诊 所和病人节约大量的资金。为了找到适合的解决方案,供应商将视野投向了预测分析技术和工具,但其分析团队还必须花时间向医生解释基于数据的治疗方案意味着 什么。
克利夫兰诊所负责企业信息管理和分析的医疗
- java 线程(一):基础篇
DavidIsOK
java多线程线程
&nbs
- Tomcat服务器框架之Servlet开发分析
aijuans
servlet
最近使用Tomcat做web服务器,使用Servlet技术做开发时,对Tomcat的框架的简易分析:
疑问: 为什么我们在继承HttpServlet类之后,覆盖doGet(HttpServletRequest req, HttpServetResponse rep)方法后,该方法会自动被Tomcat服务器调用,doGet方法的参数有谁传递过来?怎样传递?
分析之我见: doGet方法的
- 揭秘玖富的粉丝营销之谜 与小米粉丝社区类似
aoyouzi
揭秘玖富的粉丝营销之谜
玖富旗下悟空理财凭借着一个微信公众号上线当天成交量即破百万,第七天成交量单日破了1000万;第23天时,累计成交量超1个亿……至今成立不到10个月,粉丝已经超过500万,月交易额突破10亿,而玖富平台目前的总用户数也已经超过了1800万,位居P2P平台第一位。很多互联网金融创业者慕名前来学习效仿,但是却鲜有成功者,玖富的粉丝营销对外至今仍然是个谜。
近日,一直坚持微信粉丝营销
- Java web的会话跟踪技术
百合不是茶
url会话Cookie会话Seession会话Java Web隐藏域会话
会话跟踪主要是用在用户页面点击不同的页面时,需要用到的技术点
会话:多次请求与响应的过程
1,url地址传递参数,实现页面跟踪技术
格式:传一个参数的
url?名=值
传两个参数的
url?名=值 &名=值
关键代码
- web.xml之Servlet配置
bijian1013
javaweb.xmlServlet配置
定义:
<servlet>
<servlet-name>myservlet</servlet-name>
<servlet-class>com.myapp.controller.MyFirstServlet</servlet-class>
<init-param>
<param-name>
- 利用svnsync实现SVN同步备份
sunjing
SVN同步E000022svnsync镜像
1. 在备份SVN服务器上建立版本库
svnadmin create test
2. 创建pre-revprop-change文件
cd test/hooks/
cp pre-revprop-change.tmpl pre-revprop-change
3. 修改pre-revprop-
- 【分布式数据一致性三】MongoDB读写一致性
bit1129
mongodb
本系列文章结合MongoDB,探讨分布式数据库的数据一致性,这个系列文章包括:
数据一致性概述与CAP
最终一致性(Eventually Consistency)
网络分裂(Network Partition)问题
多数据中心(Multi Data Center)
多个写者(Multi Writer)最终一致性
一致性图表(Consistency Chart)
数据
- Anychart图表组件-Flash图转IMG普通图的方法
白糖_
Flash
问题背景:项目使用的是Anychart图表组件,渲染出来的图是Flash的,往往一个页面有时候会有多个flash图,而需求是让我们做一个打印预览和打印功能,让多个Flash图在一个页面上打印出来。
那么我们打印预览的思路是获取页面的body元素,然后在打印预览界面通过$("body").append(html)的形式显示预览效果,结果让人大跌眼镜:Flash是
- Window 80端口被占用 WHY?
bozch
端口占用window
平时在启动一些可能使用80端口软件的时候,会提示80端口已经被其他软件占用,那一般又会有那些软件占用这些端口呢?
下面坐下总结:
1、web服务器是最经常见的占用80端口的,例如:tomcat , apache , IIS , Php等等;
2
- 编程之美-数组的最大值和最小值-分治法(两种形式)
bylijinnan
编程之美
import java.util.Arrays;
public class MinMaxInArray {
/**
* 编程之美 数组的最大值和最小值 分治法
* 两种形式
*/
public static void main(String[] args) {
int[] t={11,23,34,4,6,7,8,1,2,23};
int[]
- Perl正则表达式
chenbowen00
正则表达式perl
首先我们应该知道 Perl 程序中,正则表达式有三种存在形式,他们分别是:
匹配:m/<regexp>;/ (还可以简写为 /<regexp>;/ ,略去 m)
替换:s/<pattern>;/<replacement>;/
转化:tr/<pattern>;/<replacemnt>;
- [宇宙与天文]行星议会是否具有本行星大气层以外的权力呢?
comsci
举个例子: 地球,地球上由200多个国家选举出一个代表地球联合体的议会,那么现在地球联合体遇到一个问题,地球这颗星球上面的矿产资源快要采掘完了....那么地球议会全体投票,一致通过一项带有法律性质的议案,既批准地球上的国家用各种技术手段在地球以外开采矿产资源和其它资源........
&
- Oracle Profile 使用详解
daizj
oracleprofile资源限制
Oracle Profile 使用详解 转
一、目的:
Oracle系统中的profile可以用来对用户所能使用的数据库资源进行限制,使用Create Profile命令创建一个Profile,用它来实现对数据库资源的限制使用,如果把该profile分配给用户,则该用户所能使用的数据库资源都在该profile的限制之内。
二、条件:
创建profile必须要有CREATE PROFIL
- How HipChat Stores And Indexes Billions Of Messages Using ElasticSearch & Redis
dengkane
elasticsearchLucene
This article is from an interview with Zuhaib Siddique, a production engineer at HipChat, makers of group chat and IM for teams.
HipChat started in an unusual space, one you might not
- 循环小示例,菲波拉契序列,循环解一元二次方程以及switch示例程序
dcj3sjt126com
c算法
# include <stdio.h>
int main(void)
{
int n;
int i;
int f1, f2, f3;
f1 = 1;
f2 = 1;
printf("请输入您需要求的想的序列:");
scanf("%d", &n);
for (i=3; i<n; i
- macbook的lamp环境
dcj3sjt126com
lamp
sudo vim /etc/apache2/httpd.conf
/Library/WebServer/Documents
是默认的网站根目录
重启Mac上的Apache服务
这个命令很早以前就查过了,但是每次使用的时候还是要在网上查:
停止服务:sudo /usr/sbin/apachectl stop
开启服务:s
- java ArrayList源码 下
shuizhaosi888
ArrayList源码
版本 jdk-7u71-windows-x64
JavaSE7 ArrayList源码上:http://flyouwith.iteye.com/blog/2166890
/**
* 从这个列表中移除所有c中包含元素
*/
public boolean removeAll(Collection<?> c) {
- Spring Security(08)——intercept-url配置
234390216
Spring Securityintercept-url访问权限访问协议请求方法
intercept-url配置
目录
1.1 指定拦截的url
1.2 指定访问权限
1.3 指定访问协议
1.4 指定请求方法
1.1 &n
- Linux环境下的oracle安装
jayung
oracle
linux系统下的oracle安装
本文档是Linux(redhat6.x、centos6.x、redhat7.x) 64位操作系统安装Oracle 11g(Oracle Database 11g Enterprise Edition Release 11.2.0.4.0 - 64bit Production),本文基于各种网络资料精心整理而成,共享给有需要的朋友。如有问题可联系:QQ:52-7
- hotspot虚拟机
leichenlei
javaHotSpotjvm虚拟机文档
JVM参数
http://docs.oracle.com/javase/6/docs/technotes/guides/vm/index.html
JVM工具
http://docs.oracle.com/javase/6/docs/technotes/tools/index.html
JVM垃圾回收
http://www.oracle.com
- 读《Node.js项目实践:构建可扩展的Web应用》 ——引编程慢慢变成系统化的“砌砖活”
noaighost
Webnode.js
读《Node.js项目实践:构建可扩展的Web应用》
——引编程慢慢变成系统化的“砌砖活”
眼里的Node.JS
初初接触node是一年前的事,那时候年少不更事。还在纠结什么语言可以编写出牛逼的程序,想必每个码农都会经历这个月经性的问题:微信用什么语言写的?facebook为什么推荐系统这么智能,用什么语言写的?dota2的外挂这么牛逼,用什么语言写的?……用什么语言写这句话,困扰人也是阻碍
- 快速开发Android应用
rensanning
android
Android应用开发过程中,经常会遇到很多常见的类似问题,解决这些问题需要花时间,其实很多问题已经有了成熟的解决方案,比如很多第三方的开源lib,参考
Android Libraries 和
Android UI/UX Libraries。
编码越少,Bug越少,效率自然会高。
但可能由于 根本没听说过、听说过但没用过、特殊原因不能用、自己已经有了解决方案等等原因,这些成熟的解决
- 理解Java中的弱引用
tomcat_oracle
java工作面试
不久之前,我
面试了一些求职Java高级开发工程师的应聘者。我常常会面试他们说,“你能给我介绍一些Java中得弱引用吗?”,如果面试者这样说,“嗯,是不是垃圾回收有关的?”,我就会基本满意了,我并不期待回答是一篇诘究本末的论文描述。 然而事与愿违,我很吃惊的发现,在将近20多个有着平均5年开发经验和高学历背景的应聘者中,居然只有两个人知道弱引用的存在,但是在这两个人之中只有一个人真正了
- 标签输出html标签" target="_blank">关于标签输出html标签
xshdch
jsp
http://back-888888.iteye.com/blog/1181202
关于<c:out value=""/>标签的使用,其中有一个属性是escapeXml默认是true(将html标签当做转移字符,直接显示不在浏览器上面进行解析),当设置escapeXml属性值为false的时候就是不过滤xml,这样就能在浏览器上解析html标签,
&nb