【MATLAB代码完整可运行】多目标微电网规划设计、混合可再生能源系统、HRES、Hybrid Renewable Energy System、多目标优化

一、问题描述

相对于化石能源等不可再生能源而言，可再生能源可以定义为自然界中能够循环产生，从而不断恢复补充并维持在一定水平的一类资源，这类资源具有取之不尽，用之不竭的特点。可再生能源如风能、太阳能的随机性不确定性等缺点导致了这些资源利用率低、利用成本高的问题。为了克服这些问题，混合可再生能源系统（HRES）被越来越多的研究与应用。HRES通过适当的组合不同类型的可再生能源与常规能源，能够有效地克服各类可再生能源不确定性的缺点，相比于包含单一可再生能源的系统它也更为可靠和经济。一个HRES系统通过配置不同形式不同数量的能源，可以实现各类能源的优势互补，克服单一能源的不稳定性、随机性，从而改善系统供能的连续性、可靠性，提高系统的整体效率。

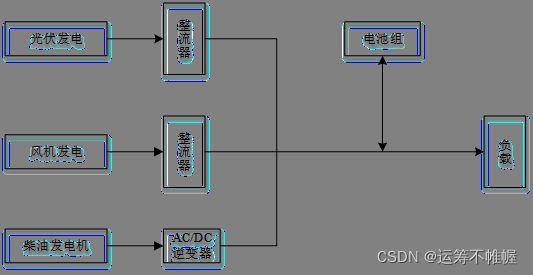
利用光、风等可再生能源发电的混合系统虽然被广泛研究，但是由于现阶段光伏系统和风机系统的安装成本依然很高，更多的研究开始考虑在混合可再生能源系统中引入柴油发电机等常规发电手段。相比于单纯的可再生能源发电系统，柴油发电机安装成本较低，并且能够充当备用电源在必要的时候满足负载功率需求。在光伏-风机-储能系统中加入柴油发电机以及相应的AC/DC逆变器，就构成了光-风-柴-储系统，其结构如图所示。
光-风-柴-储系统中可再生能源发电仍然被优先供给负载使用，满足负载之后的剩余电量给电池组充电。当可再生能源发电不能满足负载需求并且电池组达到最大放电深度时，柴油发电机才会工作以提供不足的功率需求。柴油发电机的工作虽然会消耗常规能源并产生一定的污染物排放，但其作为备用电源却可以大大提高系统供能的稳定性、连续性，提高系统的整体性能，因此这类系统被广泛研究并且正逐渐成为最普遍的混合可再生能源系统。

二、问题建模

1、光伏建模

太阳能光伏发电技术是利用太阳能的最理想方式之一。它安全、环保，没有复杂的部件。实际光伏系统的输出功率受天气和安装角度的影响很大。为了简化本部分的模型，我们只考虑光照强度和环境温度作为变量。由$N_s$个光伏板组成的光伏板链的最大输出功率可以表示为：
$$P_{pv}=N_s\cdot V_{OC}\cdot I_{SC}\cdot F_{loss}$$
$$V_{OC}=V_{STC}-K_V\cdot T_c$$
$$I_{SC}=(I_{STC}+K_I\cdot (T_C-25))\cdot \frac{S_p}{1000}$$
$$T_C=T_A+\frac{NCOT-20}{800}\cdot S_p$$
其中$K_I$和$K_V$为温度系数，$I_{STC}$和$V_{STC}$分别为标准状态下的短路电流和开路电压。$S_p$和$F_{loss}$为太阳辐射和制造商提供的包装系数。

2、风机建模

HRES的另一个重要组成部分是风力发电子系统。风力涡轮机的功率输出通常是非线性的。当风速小于切入风速时，风轮机处于关闭状态；当风速大于切入风速时，输出功率与风速大致相等。当风速大于额定风速但小于切入风速时，需要采取适当的措施限制风机的输出功率，以防止风力发电系统过载和损坏；当风速超过切入风速时，必须关闭风机以保证系统的安全。
根据风力发电机组的功率输出曲线，可以建立以下风力发电模型：

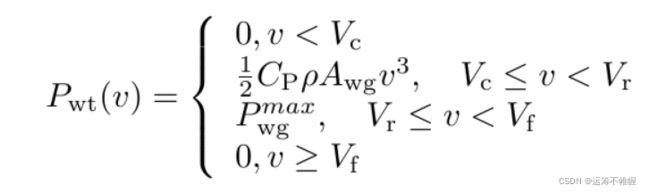
其中$v$和$C_p$是风速和风力发电机的性能系数，由制造商提供。$\rho$和$A_{wg}$分别为空气密度和转子扫过的面积。此外，$V_c$、$V_r$和$V_f$分别为切入风速、额定风速和切出风速，在本研究中根据生产商的要求，分别设定为4$m/s$、14$m/s$和20$m/s$。

3、储能系统部分

在HRES中，电池一般被用于储能。作为一个储能系统，当可再生能源发电量大于负荷需求时，电池组被用来储存多余的能量，当天气状况很差，发电量不能满足负荷时，电池组就会放电，为负荷提供能量。大多数电池模型会考虑充电状态（SOC），SOC应保持在制造商给出的最大和最小范围内，以确保安全。电池组的SOC根据可再生能源发电和负载电力需求之间的关系变化，可以表示为：
$$SOC(t+1)=SOC(t)+\frac{(P_{bat}(t)/V_{bus})\cdot \Delta t\cdot {\eta }_{bat}}{C_n}$$
$$SO{C}_{min}\le SOC(t)\le SO{C}_{max}$$
其中$P_{bat}(t)$为电池输入/输出功率（正值表示充电模式，负值表示放电模式），$V_{bus}$和$et{a}_{bat}$为直流母线电压和双向充放电效率。$C_n$（Ah）是储能系统的总额定容量。

4、柴油发电机部分

在HRES中，柴油发电机通常被用作备用能源。它只有在可再生能源发电量小于负荷需求，而电池储能系统不能满足电力不足的情况下才会工作。虽然引入柴油发电机可以进一步提高HRES的可靠性，但也会增加系统的成本。同时，柴油等化石燃料的消耗将增加有害污染物和温室气体的排放。柴油发电机的燃料消耗取决于其自身的性质。为了简化计算，可以近似假定柴油发电机的燃料消耗量$F_{cons}$是其输出功率的线性函数。
$$F_{cons}={\gamma }_1\cdot P_{dgr}\cdot \Delta t+{\gamma }_2\cdot P_{dg}\cdot \Delta t$$
其中$P_{dgr}$和$P_{dg}$是柴油发电机的额定功率和实际功率，${\gamma }_1$和${\gamma }_2$是燃料消耗曲线的系数。

5、HRES的目标函数和仿真过程

计算HRESS的目标值需要对运行过程进行模拟。为了准确计算供电损失（LPSP）、系统年成本（ACS）和燃料排放$F_{emission}$，采用了时间序列模拟方法。具体来说，上述三个目标的计算可以表示为：
$$ACS=\sum _{i\in X}(C_{inv}^i\ast N_i+C_{om}^i\ast N_i)+C_{rep}\ast N_{bat}。$$
其中$C_{inv}^i$和$C_{om}^i$是设备$i$的年成本和运行维护成本，$C_{rep}$是电池系统的替换成本。$X$是设备的集合，包括光伏、风力涡轮机、储能系统和柴油发电机。
$$LPSP=\frac{{\sum }_{t=0}^T{P}_{available}(t)<Pload(t)}{T}。$$
其中$P_{available}(t)$和$Pload(t)$是$t$时的可用功率和需要的功率。此外，为了保持系统的稳定运行，我们有$LPSP<10\%$。
$$F_{emission}=\sum _{t=0}^T{F}_{cons}(t)\ast {\eta }_{emission}.$$
其中$F_{cons}(t)$和${\eta }_{emission}$是时间$t$的燃料消耗和排放因子，它取决于柴油发电机和燃料的质量。其数值一般在2.4-2.8公斤/升之间。

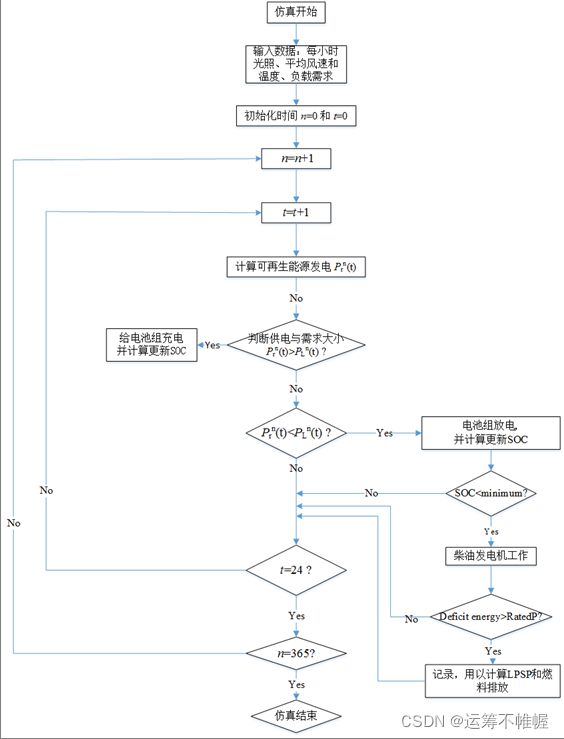
上图显示了HRES优化过程中使用的模拟流程图。在模拟程序开始时，首先给出数据，包括太阳辐射、平均风速和系统组件的相关性能指标值。然后，在每个模拟时间步骤中，优化器将根据输入数据和数学模型计算出可再生能源发电量。然后将可再生能源的输出功率与当前时刻的全部负荷需求量进行比较。如果可再生能源发电量和负载需求量相等，则跳过下面的步骤；如果供电量大于需求量，则对储能系统进行充电；如果发电量小于需求量，则首先考虑由储能系统来供应能量。一旦储能系统不能满足要求（SOC很低），柴油发电机将被打开。如果柴油发电机不能满足负荷要求，将计算LPSP。上述过程将重复进行，直到$t=T$。

三、优化算法的选择

这个问题通过建模非常清楚，我们的决策变量只有4个整数，分别为【光伏个数，风机个数，电池个数，发电机个数】，然后目标函数是三个。这是一个典型的，多约束、整数变量、多目标优化问题。因此，我们可以选择很多多目标优化算法来求解。其中，约束处理方式与我之前的博文类似，这里就不在赘述。详情请看
通用的改进遗传算法求解带约束的优化问题（MATLAB代码精讲、实际工程经验分享）
（PS.其实我主要研究的是多目标优化，对于单目标优化问题只是偶尔搞搞）

为了解这个问题，我实现了几种算法，分别是IBEA、MOEAD、NSGA2、SPEA2、MOEASES（堪称劳模）。老规矩，程序的目录如下所示：

1、数据结构设计和封装

其实主体的优化程序反而是最简单的，最难得部分是怎么合理设计数据结构、怎么计算目标函数值。这里我为了方便，直接将用到的数据打包进一个全局变量HRES里面，方便调用，具体如下：

function HRES = LoadData()
load wind_pv_temp.txt;
load Load.txt;
WG=wind_pv_temp(:,1);
S=wind_pv_temp(:,2);
temp=wind_pv_temp(:,3);

T=8760;                              %total time interval of one year
%% pv model, this model only consider the beam radiation
phi=41.65;    %地理 latitude of zaragoza in Spain, N
lamda=1.02;     %solar ecliptic longitude of zaragoza in Spain, W
I=23.44;       %地轴与轨道面倾角
belta=20;      %待优化变量 PV tilt angle

NCOT=43;                                  %额定电池工作温度
Ki=0.0038;                                %short-circuit current temperature coefficient  unit:A/C
Kv=0.05;                                 %可以再小点
%open-circuit voltage  temperature coefficient  unit:V/C
Vocstc=21;
Iscstc=7;
Vmax=17;
Imax=6.5;                                %额定功率110w
FF=Vmax*Imax/(Vocstc*Iscstc);             %fill factor
%delta:the longitude at the equator,太阳赤纬角，地球赤道面与地日中心线之间的夹角

%% the parameter of wind turbine风机参数
Vc=4;                                        %cut-in speed
Vr=14;                                       %rated wind speed
Vf=20;                                       %cut-off wind velocity
Cp=0.5;                                      %the limit of Cp is 0.593, that is Betz limit
rho=1.29;                                    %density of air  kg per m^3
r=2;                                         %radiur of wind turbine
alpha=0.15;                                  %wind speed power law efficient
Hr=10;                                       %reference height,unit:m
Ht=25;                                       %the height of wind turbine 待优化变量
Pwgr=10000;                                   %rated power 10 kw
Awg=pi*r^2;

%% battery parameter 电池参数
HRES.Cnb=500;                                   %nominal capacity of the battery, unit: Ah
HRES.volt=12;                                  %volatage ,V
HRES.Vbus=48;
HRES.rtc=0.8;                                  %roundtrip efficiency in the charging process
HRES.rtd=1;                                    %roundtrip efficiency in the discharging process
HRES.dod=0.8;
HRES.nbs=HRES.Vbus/HRES.volt;                            %number of batteries in series

%% diesel parameter
HRES.Pndg=2000;                                  %diesel nominal capacity, unit:W
HRES.afdg=0.1;                              %额定功率下燃料消耗参数，unit:l/kwh
HRES.bdg=0.25;                                 %非额定功率下燃料消耗参数
HRES.inverter_dg=0.9;                            %交流发电机逆变器效率

HRES.ef=2.5;                                     %fuel emission factor kg/l

%% power output
PV = zeros(1,T);
PWG = zeros(1,T);
for n=1:365
    delta(n)=I*sin(2*pi*(284+n)/365);
    
    for t=0:23
        i=24*(n-1)+t+1;
        tao=2*pi*(12-t)/24;
        ele(i)=sin(phi*pi/180)*sin(delta(n)*pi/180)+cos(phi*pi/180)*cos(delta(n)*pi/180)*cos(tao);
        %防止出现过小的机器数，设置精度
        if ele(i)<0.01
            ele(i)=0;
        end
        
        h(i)=asind(ele(i));                                        %结果以度表示,太阳高度角  elevation angle
        if h(i)<0||h(i)==0
            St(i)=0;
            Sp(i)=0;
        else
            St(i)=S(i)/ele(i);                                         %入射在斜面上的部分tilt
            Sp(i)=St(i)*sin((h(i)+belta)*pi/180);                               %垂直于斜面的部分，有效部分，pendicular
        end
        Tc(i)=temp(i)+(NCOT-20)*Sp(i)/800;
        Isc(i)=[Iscstc+Ki*(Tc(i)-25)]*Sp(i)/1000;
        Voc(i)=Vocstc-Kv*Tc(i);
        PV(i)=Isc(i)*Voc(i)*FF;                                     %考虑光伏个数之后的总输出功率
        
        %% wind turbine
        V(i)=WG(i)*(Ht/Hr)^alpha;
        if V(i)<Vc
            Pwg(i)=0;
        elseif V(i)>Vc&&V(i)<Vr ||V(i)==Vc
            Pwg(i)=0.5*Cp*rho*Awg*V(i)^3;
        elseif V(i)>Vr&&V(i)<Vf||V(i)==Vr
            Pwg(i)=Pwgr;
        else %V(i)>Vf||V(i)==Vf
            Pwg(i)=0;
        end
        PWG(i)=Pwg(i);                                          %考虑风机个数的总输出功率
    end
end

HRES.Ppv = PV.*2.5;
HRES.Pwg = PWG./2;
HRES.Pload = Load'.*2;

加载完成之后，封装的数据如下：

种群的数据结构设计也跟之前博客差不多，初始化种群如下：

2、目标函数的计算

剩下的就是目标函数的计算啦，按照上文提到的数学模型，很容易就能写出来：

这里特别要注意的是，为了让所有不支持约束处理技术的算法都能有效得到最优解并且对比起来更加公平，我们使用了罚函数的方法。

四、实验结果

为了获得问题的Pareto前沿，我也是使用穷举的方法遍历了一下，非常耗时间，一并开源吧。

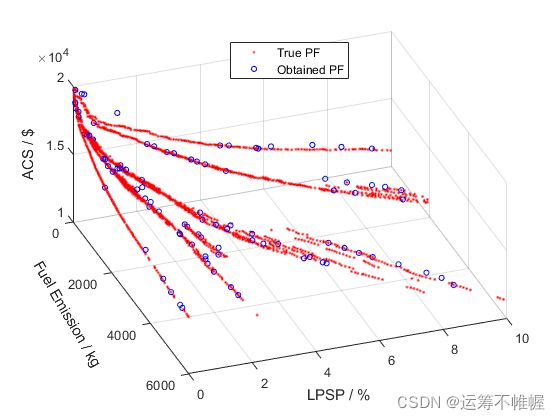
下面是不同算法的运行结果对比：

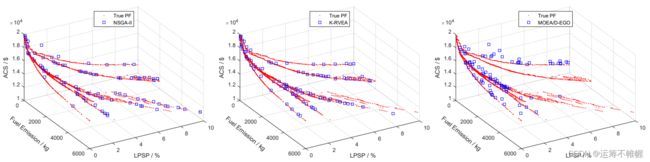
为了展示方便，提取出问题的Knee点作为最终的解。

同时将各个组件的运行状态展示一下，分了四个季节，挑选了典型日作为展示~




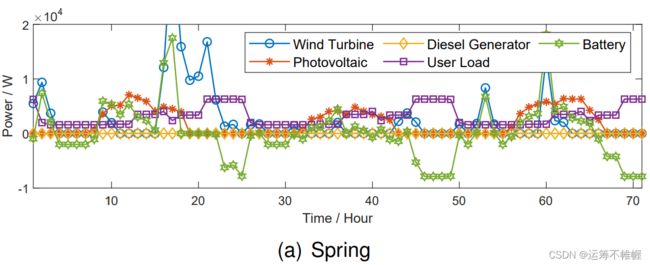
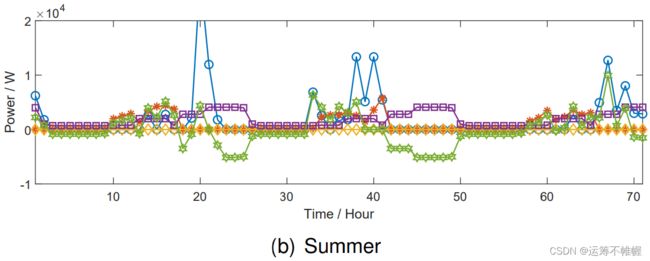
最后，博主专注于优化领域论文的复现工作，有兴趣的同学可以私信共同探讨。本次的代码因为费时比较长，采用捐赠方式获取（一杯咖啡），详情请私聊博主。