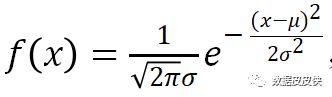python求标准差_统计知识微课堂:Python实现
微信公众号:数据皮皮侠如果你觉得该公众号对你有帮助,欢迎关注、推广和宣传
内容目录:统计知识微课堂:Python实现
一、常见统计量(期望,方差,标准差,相关系数等)二、检验正态性的方法
一、常见统计量(期望,方差,标准差,相关系数等)
为了进行统计推断,针对不同的研究目的,我们会针对样本,构造不同样本函数,这种函数在统计学中称为统计量。
常见的统计量:
Python中计算相关系数的方式有pearson和spearman两种方式,默认为pearson。连续数据、正态分布、线性关系,用pearson相关系数最恰当,也可以用spearman相关系数也可以,但效率没有pearson相关系数高。上述任一条件不满足,或者两个定序测量数据,就只能用spearman相关系数。
6、以上统计量的Python实现方法:
import pandas as pd
import tushare as ts
data1 = ts.get_hist_data('000001')#获取沪深指数数据
data2 = ts.get_hist_data('399106')#获取深证成指数据
data1.mean()#求样本1均值
data1.var()#求样本1方差
data1.std()#求样本1标准差
data1.cov()#求样本1协方差阵
data1['close'].corr(data2['close'])#求沪深指数和深证成指收盘价的相关系数
#另一种方法求相关系数
df = pd.concat([data1.close,data2.close],axis=1,keys=['data1colese','data2close']) #按列合并
t1 = df.corr()#用pearson方法求相关系数矩阵
t2 = df.corr(method = 'spearman')#用spearman方法求相关系数矩阵
print(t1)
print(t2)
plt.scatter(data1['close'], data2['close'],color = 'red')#画出两种股票收盘价的散点
二、检验正态性的方法
1、正态分布定义
若随机变量X的概率密度函数
,则称X服从期望为μ,方差为σ2的正态分布,记为X~N(μ,σ2)。当μ=0,σ=1,则称X服从标准正态分布,记为X~N(0,1)。
正态分布是一种很重要的分布,实际问题中有许多随机变量服从或近似服从正态分布(如一个人群中成年男子的身高、体重,工件的测量误差等)
2、构造正态分布
#构造标准正态分布
#构造标准正态分布
mu = 0 #期望μ
sigma = 1 # 标准差σ
x = np.arange(-5,5,0.1)
y1 = stats.norm.pdf(x,0,1)#正态分布密度函数在x处的取值
plt.plot(x,y1,'r',label='概率密度')
y2 = stats.norm.cdf(x,0,1)#正态分布的函数值
plt.plot(x,y2,'g',label='概率')
plt.legend(loc='best')
plt.title('Normal:$\mu$ = %.1f, $\sigma^2$ = %.1f' %(mu, sigma))
plt.xlabel('x')
plt.show()
3、检验方法
(1)W检验,又称S-W检验
对研究的对象总体,先提出假设认为总体服从正态分布,再将样本量为n的样本按大小顺序排列。然后由确定的显著性水平α,以及根据样本量为n时所对应的系数αi,根据公式
,计算出检验统计量W。最后查特定的正态性W检验临界值表,比较它们的大小,满足条件则接受假设,认为总体服从正态分布,否则拒绝假设,认为总体不服从正态分布。
Python实现:W检验的p值大于0.05,则认为总体服从正态分布;反之,不服从正态分布。W检验适用于样本数n小于50的样本。
# 方法一 W检验,检验正态性
#Python命令 stat, p = shapiro(data)
from scipy.stats import shapiro
import matplotlib.pyplot as plt
data = [0.86, 0.78, 0.83, 0.84, 0.77, 0.84, 0.81, 0.84, 0.81, 0.81, 0.80, 0.81,
0.79, 0.74, 0.82, 0.78, 0.82, 0.78, 0.81, 0.80, 0.81, 0.74, 0.87, 0.78]
plt.hist(data)#画出数据分布直方图
stat, p = shapiro(data)#进行W检验
print("stat为:%f" %stat,"p值为:%f" %p)
# 一般来说我们认为 p值大于0.05时,为正态分布,小于则为非正态性。故而这里为正态分布。
(2)KS检验
KS检验是比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|,当实际观测值D>D(n,α)则拒绝H0,否则则接受H0假设。
Python实现:KS检验的p值大于0.0,则认为总体服从正态分布;反之,不服从正态分布。KS检验的样本量需大于50
#方法二:使用KS检验样本量需要大于50个,检验正态性。
from scipy.stats import kstest
data = [0.86, 0.78, 0.83, 0.84, 0.77, 0.84, 0.81, 0.84, 0.81, 0.81, 0.80, 0.81,
0.79, 0.74, 0.82, 0.78, 0.82, 0.78, 0.81, 0.80, 0.81, 0.74, 0.87, 0.78]
plt.hist(data)#画出数据分布直方图
kstest(data,'norm')#进行KS检验
#statistic为D值,pvalue为p值.一般来说我们认为 p值大于0.05时,为正态分布,小于则为非正态性。
(3)作图检验
a.直方图
plt.hist(data,color = 'r')
判断方法:是否以钟型分布
b.箱线图
判断方法:观察矩形位置和中位数,若矩形位于中间位置且中位数位于矩形中间,则分布较为对称
plt.boxplot(data)#作出箱线图
c.核函数图
核密度估计是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。由于核密度估计方法不利用有关数据分布的先验知识,对数据分布不附加任何假定,是一种从数据样本本身出发研究数据分布特征的方法。因而,在统计学理论和应用领域均受到高度的重视。
seaborn的displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,能很形象地反应样本数据是否符合正态分布。
import seaborn as sns
sns.set_palette("hls")
sns.distplot(data, kde=True, color='y')