ABTest
ABtest原理及简介
-
什么是AB测试?
AB测试来源于假设检验,我们现在有两个随机均匀的样本组A,B,对其中组A做出某种改动,实验结束后分析两组用户行为数据,通过显著性检验,半段这个改动对于我们所关注的核心指标是否有显著的影响。
原理:ABtest其实就是随机均匀样本组的对照实验。
-
AB测试的一般流程
-
实验改动点确认
一般在开始实验之前,首先需要和相关的产品或者项目经理确定这个实验要验证的改动点。
-
核心指标确定
确认改动点之后,数据分析师需要设计实验中所需要去观测的一些核心指标,比如点击率、转化率等。
-
样本量、周期确定
- 确定完核心指标之后,下一步就是计算实验所需要的最少样本流量,实验样本越大,我们的结果越可信,但是对我们用户的不良影响就越大。所以我们需要计算能够显著地证明我们的策略有效的最少样本量。
- 结合目前日均活跃的用户量,计算实验持续的时间周期。
-
流量分割
-
根据实验需要对样本流量进行分流分层,保证样本的随机和均匀分布,避免出现辛普森悖论。
-
辛普森悖论:
-
辛普森悖论是指一种情况,你认为你了解两个变量之间的关系方向,但是当你考虑其他变量时,该方向似乎相反。
-
当人们眼睛两种变量(比如新生录取率与性别)是否具有相关性的时候,会分别对之前进行分组的研究。然而,在分组比较中都占优势的一方,在总评中有时反而是失势的一方。
-
-
原因:因为数据的分解(例如,将其拆分为子组)可能导致某些子组与其他子组相比具有不平衡的表示形式。这可能时由于变量之间的关系,或者仅仅时由于数据已被划分为子组的方式
-
回避方式:斟酌个别分组的权重,以一定的系数去消除以分组资料技术差异所造成的影响,同时必须了解该情境是否存在其他潜在要因而综合考虑。
-
-
AB测试灰度
需要和PM以及开发同学确认可以开始实验。一般在上线正式实验之前,会通过小流量去看一段时间的灰度实验。这个灰度实验的目的就是为了验证我们的这个改动并不会造成什么特别极端的影响。
-
AB测试上线
在灰度之后就会正式发版,等到实验周期结束,我们对实验的结果进行显著性检验。
-
效果评估验证
-
明确改动点和观测指标
-
明确改动点
实验开始之前,首先要和产品或者项目经理明确实验拿到变量时什么?要保证ABtest的**”单一因素原则“**,即每一个实验的评估的因素都是单一因素,一次实验不能糅合多个影响因素,否则会导致实验效果难以区分时哪个因素的影响。
-
明确观测指标
观测指标可以分为两种类型:
- **绝对值类指标。**直接计算就能得到单个指标,不需要多个指标计算得到。一般都是统计该指标在一段时间内的均值或者汇总值,比如DAU,平均停留时长等。这类指标一般较少作为AB测试的观测指标。
- **比率类指标。**与绝对值类指标相对应,不能直接计算得到,需要通过多个指标计算得到。比如某页面的点击率,需要先计算页面的点击数和展现数,两者相除才能得到该指标。类似的,还有一些转化率、复购率等等。ABtest观测的大部分指标的比率类指标。
区分不同类型的观测指标,是因为在接下来的样本量计算中,这两类指标的样本量计算有所差别。
样本量、实验周期计算
-
AB测试样本量计算
ABtest样本量的选取基于大数定律和中心极限定理。
- 大数定律:当试验条件不变时,随机实验重复多次以后,随机事件的频率近似等于随机事件的概率。
- 中心极限定理:对独立同分布且又相同期望和方差的n个随机变量,当样本量很大时,样本的均值近似服从标准正太分布N(0,1)
即:只要样本量足够大,样本就能够代表整体的表现。
每一个实验组所需要的样本量计算公式:
N = ( Z 1 − α 2 + Z 1 − β ) 2 ∗ σ 2 δ 2 ≈ 8 ∗ σ 2 δ 2 N = \frac{(Z_{1-\frac{\alpha}{2}}+Z_{1-\beta})^2*\sigma^2}{\delta^2}\approx\frac{8*\sigma^2}{\delta^2} N=δ2(Z1−2α+Z1−β)2∗σ2≈δ28∗σ2一般情况下:
置信水平: α = 0.05 \alpha=0.05 α=0.05 , Z 1 − α 2 = 1.96 Z_{1-\frac{\alpha}{2}}=1.96 Z1−2α=1.96
统计功效: β = 0.2 \beta=0.2 β=0.2, Z 1 − β = 0.84 Z_{1-\beta}=0.84 Z1−β=0.84
-
σ \sigma σ为样本标准差,衡量整体样本数据的波动性,可以计算样本的标准差计算得到。
-
δ \delta δ为预期实验组和对照组两组数据的差值,比如说期望点击率从20%提升到25%,那么 δ \delta δ就是5%。
-
α \alpha α,指的是犯第一类错误的概率了,把没有犯第一类错误的概率 1 − α 1-\alpha 1−α称为置信水平。
-
β \beta β,指的是第二类错误的概率,把统计功效定义为 1 − β 1-\beta 1−β,统计功效的取值为0.8。
当观测的指标为绝对值类型/比率型指标时,样本的标准差的计算公式有所差异,
当观测指标为绝对值类指标时:
σ 2 = 2 ∗ ∑ 1 n ( X i − X ‾ ) 2 n − 1 \sigma^2 = \frac{2*\sum^n_1(X_i-\overline{X})^2}{n-1} σ2=n−12∗∑1n(Xi−X)2
其中: n为样本数量, X ‾ \overline{X} X为样本均值。
当观测指标为比率类指标时:
σ 2 = P A ( 1 − P A ) + p B ( 1 − P B ) \sigma^2 = P_A(1-P_A) + p_B(1-PB) σ2=PA(1−PA)+pB(1−PB)
其中: P A , P B P_A, P_B PA,PB分别为对照组和实验组的观测数据。
其中PA、PB分别为对照组和实验组的观测数据,举个栗子,我们希望点击率从20%提升到25%,那么PA=20%,PB=25%,δ=5%。
如果上面的公式觉得不好理解,那我们就举个栗子计算一下!
栗子1-对于绝对值指标:
某商品详情页平均停留时长的标准差是20秒,优化了商品详情页后,预估至少有5秒的绝对提升,AB测试每个组需要的最少样本量:
σ=20,δ=5
每个组所需的最少样本量 = 8 * 20 *20 *2 /5 *5 = 256
栗子2-对于比率类指标:
某商品详情页点击率20%,优化了该功能后,预期点击率提升到25%,AB测试每个组需要的最少样本量:
对照组PA:20%,实验组PB:25%
每个组所需的最少样本量 = 8 * (20%(1-20%)+25%(1-25%))/ (25%- 20%)^2=1030
计算出单个实验组所需的样本量,若有多个实验组,乘以实验组的个数就可以得到最终的样本量。
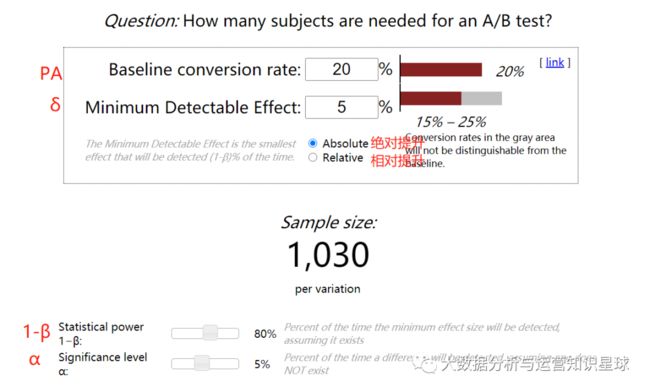
一个比较常见且好用的在线计算工具:**Evans awesome AB Tools:**https://www.evanmiller.org/ab-testing/sample-size.html,它的界面是这样的
第一个需要我们确定的是baseline conversion rate,这个baseline conversion rate指的是在开始实验之前,对照组本身真实的表现情况,如果在这个实验中想要去观测的是点击率变化,那么baseline conversion rate 就是原来的点击率是多少,对应的就是前面提到的PA。
第二个需要我们确定的是minimum detectable effect,这个指的就是你的改动预期带来的提升,举之前的例子,我们希望通过优化,点击率从20%提升到25%,那么这个绝对(absolute)提升是5%(25%-20%),如果选择相对(relative)提升,就是30%(26%-20%)/20%=30%,这个对应的就是前面提到的δ。
除了这两个参数之外,还有就是significance level,也就是我们所说的显著性水平,这个就对应前面的第一类错误的概率,也就是α,一般为5%。还有statistical power,也就是我们前面所说的统计功效,statistical power一般用1-β来表示,这里的话也就是80%,和之前保持一致。
**Evans AB Tools这个工具不仅可以计算AB测试的样本量,AB测试结果的显著性分析验证也可以使用,卡方检验、T检验、方差分析等,应有尽有,从样本量计算到结果验证,一个工具就搞定了!**我们后面的结果验证就是用这个工具进行的,这里就不再展开了。
AB测试流量分割
-
辛普森悖论
- 细分的结果和总计的结果相悖。
- 正确的试验实施方案里,除被测试的变量外,其他可能影响结果的变量的比例都应该保持一致,这就需要对流量进行均匀合理的分割。
-
分流分层原理
-
分流,用户分流是指按照地域、性别、年龄等把用户均匀地分为几个组,1个用户只能出现在一个组中。
-
分层,**同一份流量可以分布在多个实验层,也就是说同一批用户可以出现在不同的实验层,**前提是各个实验层之间无业务关联,保证这一批用户都均匀地分布到所有的实验层,达到用户“正交”的效果就可以。所谓的正交分层,其实可以理解为互不影响的流量分层, 从而实验流量复用的效果。
-
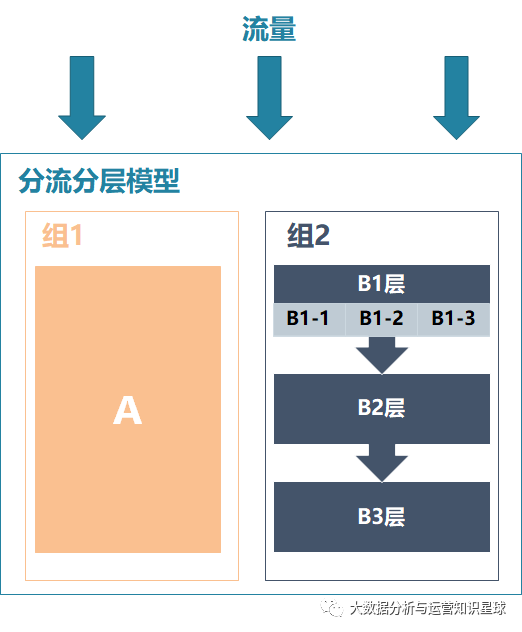
分流分层模型
-
分流:组1、组2通过分流的方式分为2组流量,此时组1和组2是互斥 ,即组1 + 组2 = 100%试验流量。
-
分层:流量流过组2中的B1层、B2层、B3层时,B1层、B2层、B3层的流量都是与组2的流量相等,相当于对组2的流量进行了复用,即B1层=B2层=B3层=组2
-
扩展:流量流过组2中的B1层时,又把B1层分为了B1-1,B1-2,B1-3,此时B1-1,B1-2,B1-3之间又是互斥的,即B1-1层 + B1-2层 + B1-3层 = B1层。
根据以上规则我们可以不断地在此模型中增加组、层,并且可以互相嵌套。这要与实际的业务相匹配,拆分过多的结构可能会把简单的业务复杂化,拆分过少的结构又可能不满足实际业务。
-
-
使用场景
用于某些对所有功能都有影响的运营活动,比如春节的红包运营,由于活动时整体的,UI,策略,内容等模块都会配合修改,因此要评估春节红包活动的时候就会使用组1来评估。而剩余的组2的流量,则回划分为多个层,比如UI层,推荐测率曾,内容模块层等,这几层基本上时没有任何的业务关联度的,即使共用相同的流量(流量正交)页不会对实际的业务造成结果。
-
AB测试效果验证
-
测试效果显著性检验
AB测试后,我们需要对AB测试的结果进行显著性检验,从而判断改动是否对我们的核心指标产生了显著差异。
举个栗子,仍以点击率为例,我们运行AB测试一周,分别对1000个样本进行了测试。对照组A的点击率为7.5%,B的点击率为9%,如下表:
我们能否给出结论说B比A好,改动是有效果的呢?有多大的可能是因为一些随机的因素导致这样的差异呢?
假设检验可以有效地帮助我们回答这个问题。首先假设改动没有效果,即B的效果不会比A好,然后试图通过样本测试的结果来验证这个假设,如果样本足以推翻假设,那么我们就可以认为改动有效果,否则我们需要继续实验或者干脆就接受这个假设,把B方案扔掉了事。
由于我们实验的样本一般都较大(大于30),所以我们使用Z检验来检验差异显著性(样本量较小时,我们一般用T检验,对此有疑问感兴趣的同学可以查阅相关资料)。
-
Z检验
- 样本统计量Z值
Z检验时一种适用于大样本(样本容量大于30)的两组平均数之间差异显著性检验的方法。它是通过计算两组平均数直接按差的Z值与理论Z值相比较,看是否大于规定的理论Z值,从而判断两组平均数的差异是否显著。
其一般步骤如下:
第一步:建立原假设 H0:μ1 = μ2 ,即先假定两组平均数之间没有显著差异,
第二步:计算统计量Z值,对于不同类型的问题选用不同的统计量计算方法,通过检验两组样本平均数的差异性,判断它们各自代表的总体的差异是否显著。
与计算样本量相似,当观测的指标为绝对值类型/比率型指标时,Z值的计算公式有所差异。
当观测指标为绝对类指标时:
Z = X A ‾ − X B ‾ σ A 2 N A + σ B 2 N B Z= \frac{\overline{X_A}-\overline{X_B}}{\sqrt{\frac{\sigma^2_A}{N_A}+\frac{\sigma^2_B}{N_B}}} Z=NAσA2+NBσB2XA−XB
其中:
X A ‾ 、 X B ‾ \overline{X_A}、\overline{X_B} XA、XB分别为A、B组样本的均值
σ A 2 、 σ B 2 \sigma^2_A、\sigma^2_B σA2、σB2分别为A、B组样本的方差
N A 、 N B N_A、N_B NA、NB分别为A、B组样本的数量
当观测指标为比率类指标时:
Z = P A − P B P A ( 1 − P A ) N A + P B ( 1 − P B ) N B Z = \frac{P_A - P_B}{\sqrt{\frac{P_A(1-P_A)}{N_A}+\frac{P_B(1-P_B)}{N_B}}} Z=NAPA(1−PA)+NBPB(1−PB)PA−PB
其中:
P A 、 P B P_A、P_B PA、PB分别为A、B组样本的比率
N A 、 N B N_A、N_B NA、NB分别为A、B组样本的数量
计算公式类似,知识对于绝对值/比率型指标,方差的计算方式有些差异而已。
- 理论Z值
样本的统计量Z值可以通过以上的公式进行计算,理论Z值可以通过查询Z值表获得,更方便的一种方法,可以通过Excel的NORM.S.INV函数直接计算,如下是常用的置信水平90%、95%、99%下的理论Z值。
- 样本统计量Z值vs理论Z值比较
假设通过以上公式计算的统计量Z值 = 1.22,小于我们设定95%置信水平对应理论Z值1.96,也就是说我们暂无法判断这种差异性是显著的,所以上述样本不足以得出B比A好的结论。
- 继续实验
由于无法得出B比A好的结论,此时需要做更多实验。
于是,我们又做了一周,A和B分别得到了3000个样本,对照组和实验组转化率不变。这个时候我们有信心认为B比A好了吗?
仍然是套用上述公式求统计量Z值= 2.66。超出了我们设定的95%置信水平对应理论Z值1.96,这个时候我们有了足够的信心来相信B比A好。到此为止,实验结束。
- 用工具直接验证
分别输入对照组和实验组的比率类指标对应的分子、分母和置信水平Confidence level(一般95%)。
在第一周的实验中,对照组A对应的分子、分母为75/1000(转换率为7.5%),实验组B的对应的分子、分母为90/1000(转换率为95),设置置信水平Confidence level 为95%,得出的结果如下:两组无显著性差异!
又进行了一周实验,对照组A对应的分子、分母为225/3000(转化率为7.5%),实验组B的对应的分子、分母为270/3000(转化率为9%),置信水平Confidence level仍为95%,得出结论:两组有显著差异,且实验组B效果更好!