数据挖掘（七） DBSCAN聚类算法

数据挖掘（七） DBSCAN聚类算法

DBSCAN是一种非常著名的基于密度的聚类算法。其英文全称是 Density-Based Spatial Clustering of Applications with Noise，意即：一种基于密度，对噪声鲁棒的空间聚类算法。直观效果上看，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

基于密度的簇是密度相连的点的集合

DBSCAN算法具有以下特点：

• 基于密度，对远离密度核心的噪声点鲁棒

• 无需知道聚类簇的数量

• 可以发现任意形状的聚类簇

DBSCAN通常适合于对较低维度数据进行聚类分析。

1.基本概念

DBSCAN的基本概念可以用1，2，3，4来总结。

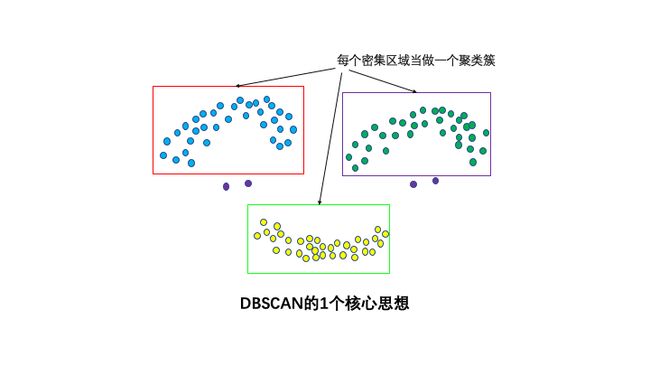
1个核心思想：基于密度。直观效果上看，DBSCAN算法可以找到样本点的全部密集区域，并把这些密集区域当做一个一个的聚类簇。

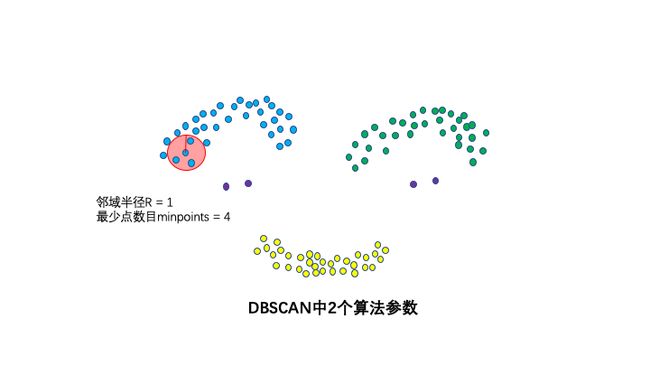
2个算法参数：邻域半径R和最少点数目MinPoints。这两个算法参数实际可以刻画什么叫密集：当邻域半径R内的点的个数大于最少点数目R时，就是密集。

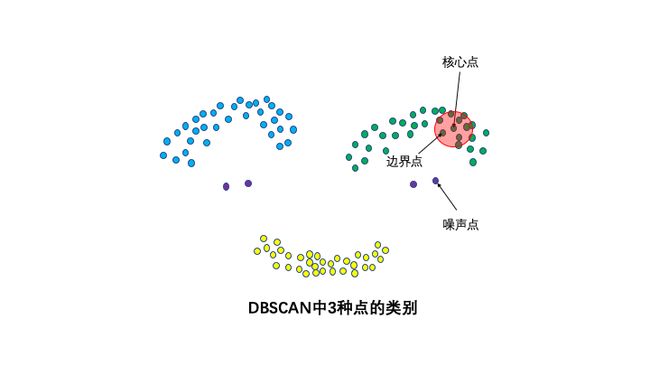
3种点的类别：核心点，边界点和噪声点。邻域半径R内样本点的数量大于等于minpoints的点叫做核心点。不属于核心点但在某个核心点的邻域内的点叫做边界点。既不是核心点也不是边界点的是噪声点。

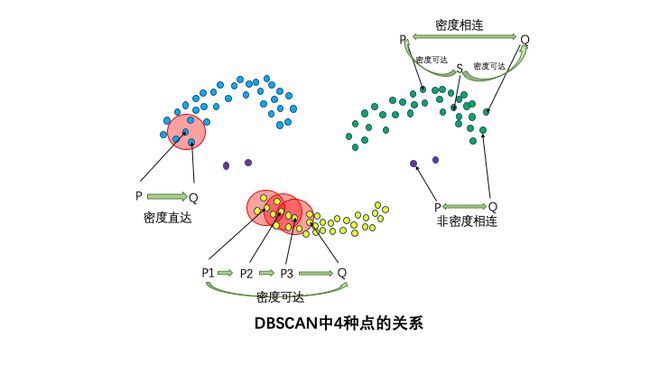
4种点的关系：密度直达，密度可达，密度相连，非密度相连。

如果P为核心点，Q在P的R邻域内，那么称P到Q密度直达。任何核心点到其自身密度直达，密度直达不具有对称性，如果P到Q密度可达，那么Q到P不一定密度可达。

如果存在核心点P2，P3，……，Pn，且P1到P2密度直达，P2到P3密度直达，……，P(n-1)到Pn密度直达，Pn到Q密度直达，则P1到Q密度可达。密度可达也不具有对称性。

如果存在核心点S，使得S到P和Q都密度可达，则P和Q密度相连。密度相连具有对称性，如果P和Q密度相连，那么Q和P也一定密度相连。密度相连的两个点属于同一个聚类簇。

如果两个点不属于密度相连关系，则两个点非密度相连。非密度相连的两个点属于不同的聚类簇，或者其中存在噪声点。

2.算法步骤

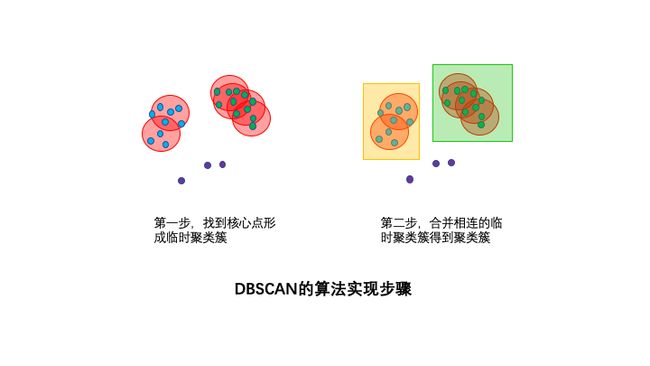
DBSCAN的算法步骤分成两步。

1，寻找核心点形成临时聚类簇。

扫描全部样本点，如果某个样本点R半径范围内点数目>=MinPoints，则将其纳入核心点列表，并将其密度直达的点形成对应的临时聚类簇。

2，合并临时聚类簇得到聚类簇。

对于每一个临时聚类簇，检查其中的点是否为核心点，如果是，将该点对应的临时聚类簇和当前临时聚类簇合并，得到新的临时聚类簇。

重复此操作，直到当前临时聚类簇中的每一个点要么不在核心点列表，要么其密度直达的点都已经在该临时聚类簇，该临时聚类簇升级成为聚类簇。

继续对剩余的临时聚类簇进行相同的合并操作，直到全部临时聚类簇被处理。

3.实验

# 1. 寻找核心点形成临时聚类簇。
# 扫描全部样本点，如果某个样本点R半径范围内点数目>=MinPoints，则将其纳入核心点列表，并将其密度直达的点形成对应的临时聚类簇。
# 2，合并临时聚类簇得到聚类簇。
# 对于每一个临时聚类簇，检查其中的点是否为核心点，如果是，将该点对应的临时聚类簇和当前临时聚类簇合并，得到新的临时聚类簇。
# 重复此操作，直到当前临时聚类簇中的每一个点要么不在核心点列表，要么其密度直达的点都已经在该临时聚类簇，该临时聚类簇升级成为聚类簇。
# 继续对剩余的临时聚类簇进行相同的合并操作，直到全部临时聚类簇被处理。
class DBscan:
    def __init__(self,eps,MinPts):
        self.eps = eps
        self.MinPts = MinPts
    
    # 返回样本点eps半径范围内的索引
    def regionQuery(self,i,x):
        # 计算当前点与其他所有点的距离
        diff = i - x
        distances = np.sqrt(np.square(diff).sum(axis=1))
        #返回满足邻域点的索引
        return list(np.where(distances <= self.eps)[0])
    
    def fit(self,x):

        #初始标签为-1
        label = -1
        m =len(x)
        #初始化所有样本点所属的类别，定为-1
        cluster = [-1 for i in range(m)]
        #已访问样本点
        visited = []   

        for p in range(m):   # 遍历每个点
            if p not in visited:  # 如果没有访问过则执行

                NeighborPts = self.regionQuery(x[p],x)  # NeighborPts是p的领域点

                '''1. 寻找核心点形成临时聚类簇。'''
                if len(NeighborPts) < self.MinPts: # 半径范围内点数目 < MinPoints，跳过
                    #默认标记为-1，后面可能会被加入到其他的邻域内，成为一个密度可达点
                    continue

                else:    # 半径范围内点数目>=MinPoints，即当前点为核心点
                    label += 1
                    cluster[p] = label

                    '''2，合并临时聚类簇得到聚类簇。'''
                    #列表NeighborPts是动态变化的，添加没有访问过的全部密度可达点，划分到一个簇
                    for p_1 in NeighborPts: # 对核心点的领域点（即临时聚类簇）操作
                        if p_1 not in visited:

                            visited.append(p_1)  # 标记访问
                            Ner_NeighborPts = self.regionQuery(x[p_1],x) # 返回每个领域点半径范围内的点

                            if len(Ner_NeighborPts) >= self.MinPts:  # 检查每个领域点半径范围内的点是否满足数量要求
                                for a in Ner_NeighborPts:            # 满足则将这些领域范围内的点加入NeighborPts
                                    if a not in NeighborPts:
                                        NeighborPts.append(a)   #使得NeighborPts一直更新，下次检查领域范围内的点的领域点是否满足要求，一直扩张，直到无法扩张
                                        
                            #同时把p_1的类别改为label
                            cluster[p_1] = label
        return cluster

x1,y1 = make_circles(n_samples=5000,factor=0.6,noise=0.05,random_state=2020)
x2,y2 = make_blobs(n_samples=1000,n_features=2,centers=[[1.2,1.2]],cluster_std=0.1,random_state=9)
x1 = np.concatenate((x1,x2))
 
Dbscan =DBscan(eps=0.1,MinPts=10)
y_pred = Dbscan.fit(x1)
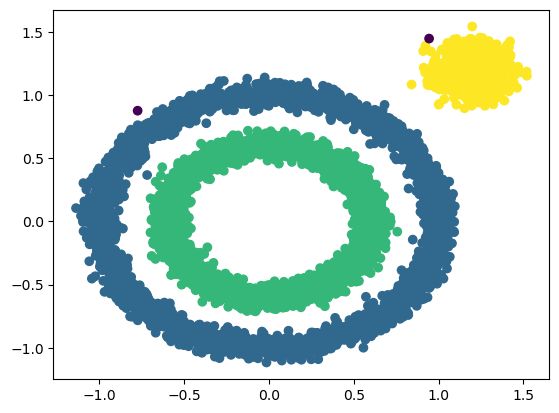
plt.scatter(x1[:,0],x1[:,1],c=y_pred,marker='o')
plt.show()

与sklearn对比：

model = DBSCAN(eps=0.1,min_samples=10)
y_preds = model.fit_predict(x1)
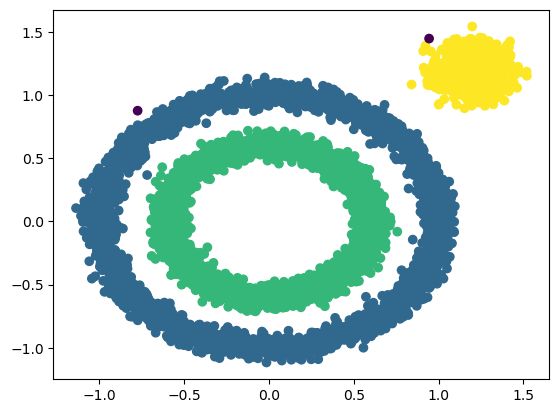
plt.scatter(x1[:,0],x1[:,1],c=y_preds,marker='o')
plt.show()

刚才验证大数据集时，为什么sklearn速度比较快，是因为：

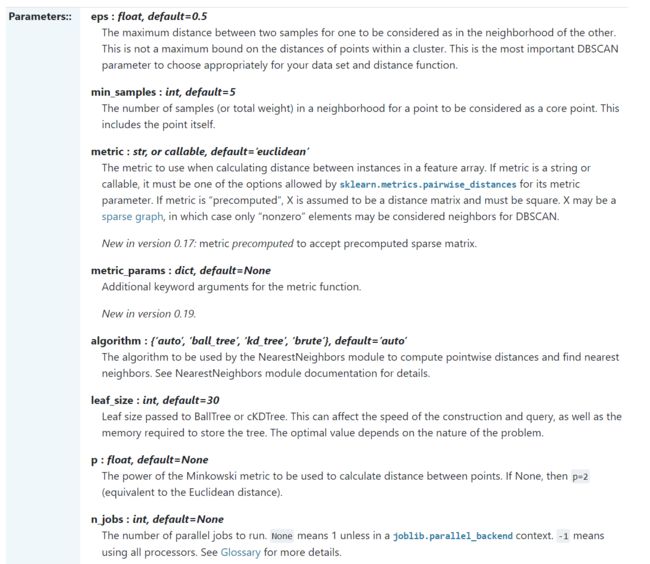
参数‘“algorithm”，算法一共有三种，第一种是蛮力实现，第二种是KD树实现，第三种是球树实现。K近邻法(KNN)中也是这样，一共有4种可选输入，‘brute’对应蛮力实现，也就是我们这种，‘kd_tree’对应第二种KD树实现，‘ball_tree’对应第三种的球树实现， ‘auto’则会在上面三种算法中做权衡，选择一个拟合最好的最优算法。需要注意的是，如果输入样本特征是稀疏的时候，无论我们选择哪种算法，最后scikit-learn都会去用蛮力实现‘brute’。

默认的距离也是欧氏距离。

和传统的K-Means算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点，这点和BIRCH算法类似。

那么我们什么时候需要用DBSCAN来聚类呢？一般来说，如果数据集是稠密的，并且数据集不是凸的，那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的，则不推荐用DBSCAN来聚类。

下面对DBSCAN算法的优缺点做一个总结。

DBSCAN的主要优点有：

1） 可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

2） 可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

3） 聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

2） 如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。

3）
调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵ，邻域样本数阈值MinPts联合调参，不同的参数组合对最后的聚类效果有较大影响。